Моделирование распределений. Освоение методов имитации случайных величин на компьютере

ЛАБОРАТОРНАЯ РАБОТА N 6

  Моделирование распределений

1.Цель и задачи.

Освоение методов имитации случайных величин на компьютере.

2.Теоретические сведения.

Пусть X - случайная величина, F(x)=P{X<x}, ее функция распределения,

f(x)- плотность. Задача имитации случайной величины  X на компьютере заключается в написании программы, которая бы работала следующим образом.

При обращении к программе она возвращает некоторое число X.

При N-кратном обращении будет получена последовательность

                                              ,                                                           (1)

статистические свойства которой такие же, как у выборки из N  значений случайной величины X.  Например, задавшись каким-либо значеиием   x

подсчитаем количество M чисел в последовательности (1), меньших  x,

мы получим, что 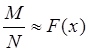. Или, если по данным (1) построить гистограмму, то она будет близка к графику плотности   f(x)..

В лабораторной работе 4 рассмотрена случайная величина  U,  равномерно распределенная на отрезке   [0,1], и программа ее имитации. Эта случайная величина называется    базовой. Процедуры имитации других случайных величин основываются на подходящем преобразовании базовой. Рассмотрим два основных метода.

Метод обратной функции

Для простоты будем предпологать функцию распределения  F(x) строго возрастающей, так что существует обратная функция . Метод обратной функции основан на следующем простом утверждении: если U- базовая случайная величина, то случайная величина

                                                                                                          (2)

имеет распределение F(x). Действительно,

                                     

Соотношение (2) можно записать также в виде

                                                                                                              (3)

то есть значение  X находится как решение уравнения (3).

 Пример.

Случайная величина  T  имеет показательное распределение, ее плотность равна  . Функция распределения  равна .

Соотношение (3) принимает вид , откуда  .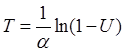

Так как случайная величина 1-U  имеет то же распределение, что и U

(равномерное на отрезке   [0,1], то последнее выражение можно упростить

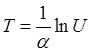                                                                                                                (4)

Программа для выработки значений случайной величины с показательным распределением может выглядеть примерно так.

Программа 5

/* имитация показательного распределения */

double expo(double alpha)

{

  return (-1.0/alpha)*log(uni());

}

Метод исключения

Метод предполагает, что плотность случайной величины  X сосредоточена на отрезке  [a,b] и ограничена: .   (Таким условиям удовлетворяют рассматриваемые далее бета-плотности.)

Метод исключения состоит в следующем. В прямоугольнике

                                                                  

равномерно рассеиваются точки  (x,y)

                                                         

Точки, попадающие выше графика   y=f(x)   исключаются из рассмотрения, так что фактически точки равномерно рассеиваются в области

                                                          

Если точка  (x,y)  попала под график, то ее первая координата  x    возвращатся в качестве значения случайной величины.

Вероятность того, что вычисленное таким образом значение  попадет  в промежуток    равна площади области

                                                           , как это и требуется для случайной величины  X.

 Пример.

                                                     

Это так называемая  бета-плотность с параметрами 4 и 3. Она достигает максимального значения при x=0,6  и это значение равно 2,0736.

Программа имитации случайной величины с этой плотностью может выглядеть примерно так.

Программа 6

/* имитация бета-распределения с параметрами 4,3*/

double beta43()

{

  double x,y;

  do {

    x=uni();

    y=2.0736*uni();

  } while(y>60*x*x*x*(1-x)*(1-x));   

  return x;

}

Задание.

1. Разработать процедуры имтации случайных продолжительностей работ для вашего задания.

2.Написать программы имитации.

3. Используя лабораторную работу 5, построить гистограммы ваших распределений и сравнить их с плотностью.

Оформление отчета.

Отчет должен содержать:

- графики плотностей случайных величин из вашего задания;

- тексты программ имитации с пояснениями.