





Приобретение навыков решения краевых задач для обыкновенных дифференциальных уравнений вариационными методами.
ТЕОРЕТИЧЕСКАЯ СПРАВКА
Общий вид краевой задачи
![]() , (1)
, (1)
где x Î[a, b], p, r, f – известные функции, ![]() – непрерывны на [a, b],
– непрерывны на [a, b], ![]() на [a, b].
на [a, b].
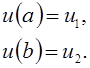 (2)
(2)
Задачу можно представить в еще более общем виде:
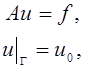
При решении рассмотрим также следующую постановку

Функцию v будем искать в виде
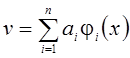 ,
(3)
,
(3)
где ![]() образуют базис в энергетическом
пространстве оператора А и удовлетворяют краевому условию (2¢). Искомая функция здесь представлена в виде
образуют базис в энергетическом
пространстве оператора А и удовлетворяют краевому условию (2¢). Искомая функция здесь представлена в виде
u = w + v,
(4) где w – известная функция, такая, что ![]() . Рекомендуется использовать
функцию вида
. Рекомендуется использовать
функцию вида ![]() , но это не является
обязательным условием. Необходимо лишь выполнение условий на границе
, но это не является
обязательным условием. Необходимо лишь выполнение условий на границе
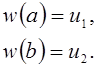
Функции ![]() будем
строить на основе рядов
будем
строить на основе рядов ![]() вида
вида
1). ![]() ,
,
2). ![]() .
.
Тогда ![]() будем
искать в виде
будем
искать в виде
![]() , где
, где ![]() – известная функция, такая, что
– известная функция, такая, что
![]() и
и ![]() на
(a, b). Для ряда 1) наиболее простой вид функции g
на
(a, b). Для ряда 1) наиболее простой вид функции g
![]() ;
;
для ряда 2)
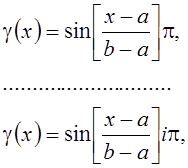
i = 1, 2, ….
Запишем уравнение (1¢):
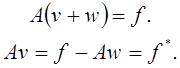
Методы получения коэффициентов ![]() :
:
I. Метод Ритца.
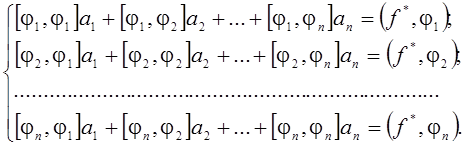
Здесь
![]()
где 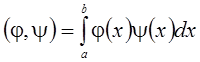 .
.
II. Метод наименьших квадратов.
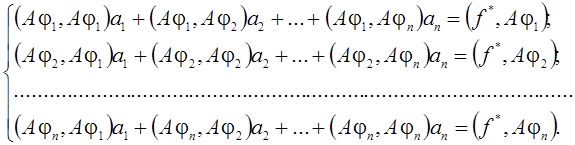
> restart;
Функция, задающая оператор А:
> A:=(u)->-(x+1)*diff(u,x$2)-diff(u,x)+(x-1)*u;
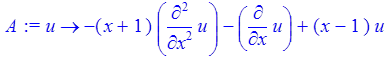
Функция, определяющая скалярное произведение
> ScalMult:=(U,V)->int(U*V,x=a..b);
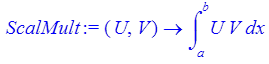
> a:=1;
b:=2;
![]()
![]()
Процедура построения функции U
> Main:=proc(Flag1,Flag2,n)
local f,w,v,v0,u,Xi,Gamma,Phi,Asd,Bsd,an,i,j;
f:=x-x*x;
w:=-x+3;
Asd:=array(1..n,1..n);
Bsd:=array(1..n);
an:=array(1..n);
if Flag1=0 then Xi:=(n)->x^n;
Gamma:=(x-a)*(b-x);
Phi:=(n)->Xi(n)*Gamma
else Xi:=(n)->sin(n*x);
Gamma:=(n)->sin((x-a)/(b-a)*n*x);
Phi:=(n)->Xi(n)*Gamma(n);
end if;
if Flag2=0
then
for i from 1 to n do
for j from 1 to n do
Asd[i,j]:=ScalMult(A(Phi(i)),Phi(j));
end do;
Bsd[i]:=ScalMult(A(f-A(w)),Phi(i));
end do
else
for i from 1 to n do
for j from 1 to n do
Asd[i,j]:=ScalMult(A(Phi(i)),A(Phi(j)));
end do;
Bsd[i]:=ScalMult(A(f-A(w)),A(Phi(i)));
end do;
end if;
an:=evalm(Bsd&*(Asd)^(-1));
v0:=0;
for i from 1 to n do
v:=v0+evalf(an[i])*Phi(i);
v0:=v;
end do;
u:=v+w;
end proc:
Результаты вызова процедуры Main:
1. Функция U строится с помощью степенного ряда; коэффициенты ![]() находятся методом Ритца:
находятся методом Ритца:
> Main(0,0,4);
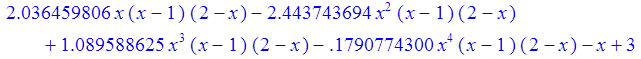
2. Функция
U строится с помощью степенного ряда;
коэффициенты ![]() находятся методом наименьших квадратов:
находятся методом наименьших квадратов:
> Main(0,1,4);
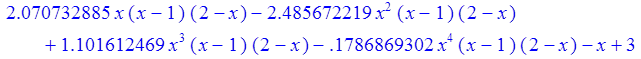
3. Функция U строится с помощью тригонометрического ряда; коэффициенты ![]() находятся методом Ритца:
находятся методом Ритца:
> Main(1,0,2);
![]()
4. Функция U строится с помощью тригонометрического ряда; коэффициенты ![]() находятся методом наименьших квадратов:
находятся методом наименьших квадратов:
> Main(1,1,2);
![]()
Процедура нахождения невязки межу рядами U(2n) и U(n) при равномерном разбиении отрезка [a, b] шагом h = 0,1:
i:=0:
J1:=Main(0,0,n):
J2:=Main(0,0,2*n):
x:=a:
while x < b do
i:=i+1:
x:=x+0.1:
Z[i]:=abs(J2-J1);
end do:
Погрешности вида ![]() для каждой функции U при различных n:
для каждой функции U при различных n:
1. Степенной ряд; метод Ритца:
а). n = 1
> print(Z);
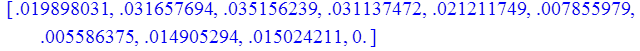
b). n = 2
> print(Z);
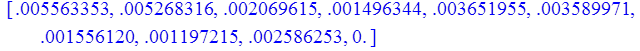
c). n = 4
> print(Z);
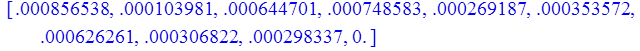
d). n = 8
> print(Z);
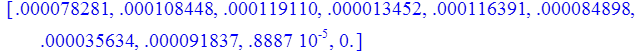
2. Степенной ряд; метод наименьших квадратов:
a). n = 1
> print(Z);
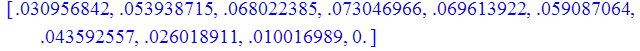
b). n = 2
> print(Z);
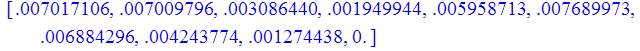
c). n = 4
> print(Z);
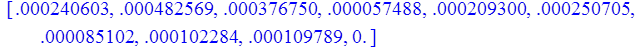
d). n = 8
> print(Z);
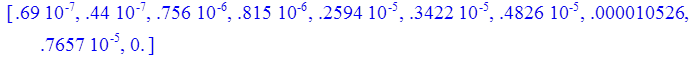
3. Тригонометрический ряд; метод Ритца:
n = 1
> print(Z);
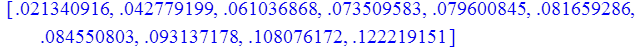
4. Тригонометрический ряд; метод наименьших квадратов:
n = 1
> print(Z);
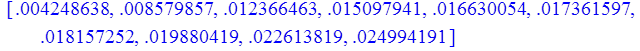
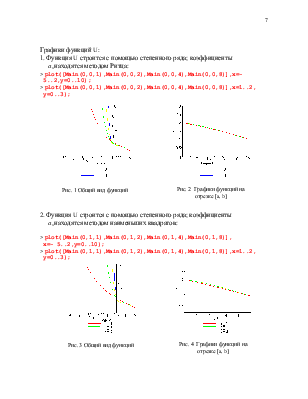
Графики функций U:
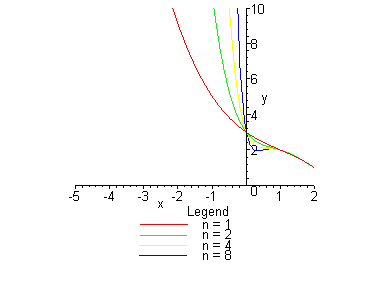
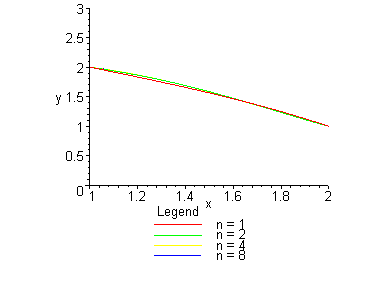
1. Функция U строится с помощью степенного ряда; коэффициенты ![]() находятся методом Ритца:
находятся методом Ритца:
> plot([Main(0,0,1),Main(0,0,2),Main(0,0,4),Main(0,0,8)],x=-
5..2,y=0..10);
> plot([Main(0,0,1),Main(0,0,2),Main(0,0,4),Main(0,0,8)],x=1..2,
y=0..3);
|
||||
|
||||
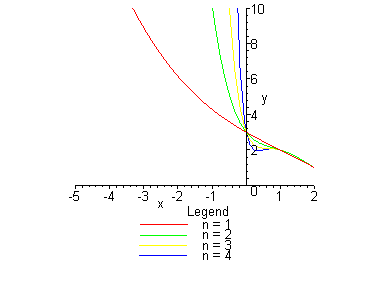
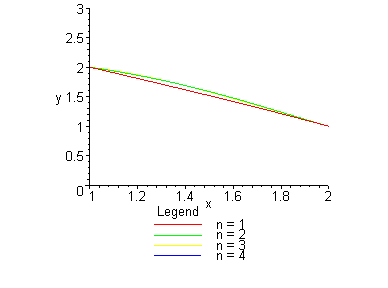
2. Функция U строится с помощью степенного ряда; коэффициенты ![]() находятся методом наименьших квадратов:
находятся методом наименьших квадратов:
> plot([Main(0,1,1),Main(0,1,2),Main(0,1,4),Main(0,1,8)],
x=- 5..2,y=0..10);
> plot([Main(0,1,1),Main(0,1,2),Main(0,1,4),Main(0,1,8)],x=1..2,
y=0..3);
|
|
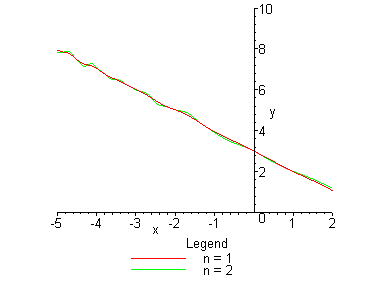
3. Функция U строится с помощью тригонометрического ряда; коэффициенты ![]() находятся методом Ритца:
находятся методом Ритца:
> plot([Main(1,0,1),Main(1,0,2)],x=-5..2,y=0..10);
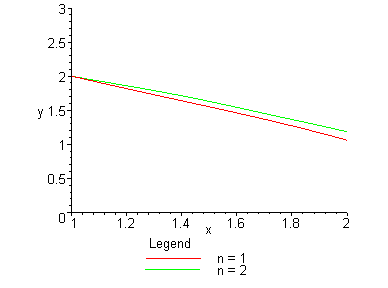
> plot([Main(1,0,1),Main(1,0,2)],x=1..2,y=0..3);
|
|
||||
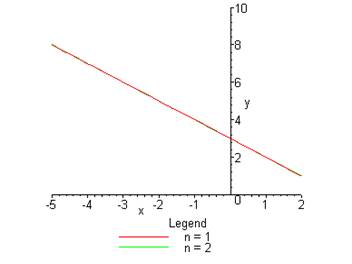
4. Функция U строится с помощью тригонометрического ряда; коэффициенты ![]() находятся методом наименьших квадратов:
находятся методом наименьших квадратов:
> plot([Main(1,1,1),Main(1,1,2)],x=-5..2,y=0..10);
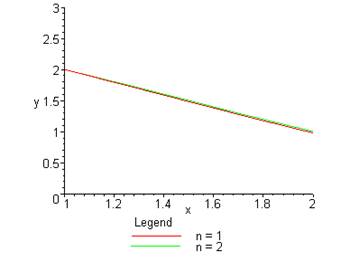
> plot([Main(1,1,1),Main(1,1,2)],x=1..2,y=0..3);
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.