




Математические модели в естествознании
1. Для нестационарного течения в общем случае: Ответ: 2) траектории частиц не совпадают с линиями тока.
2. Какая из указанных функций не может служить потенциалом течения
несжимаемой жидкости:
Ответ: 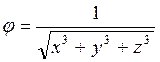 .
.
3. Какое из приведенных ниже выражений является верным:
Ответ: 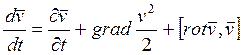 .
.
4. Уравнение Навье-Стокса движения линейно-вязкой жидкости следует из: Ответ: закона изменения количества движения.
5. Число Рейнольдса определяется выражением:
Ответ: ![]() .
.
6. Число Фруда определяется выражением:
Ответ: ![]() .
.
7. Число Эйлера определяется выражением:
Ответ: 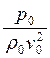 .
.
8. В безразмерном виде справедлива запись:
Ответ: 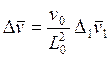 .
.
9. Течение Куэтта – это: Ответ: течение вязкой жидкости между пластинами, одна из которых неподвижна, а другая движется с постоянной скоростью.
10. Пусть ![]() - некоторая функция
эйлеровых переменных
- некоторая функция
эйлеровых переменных ![]() и времени
и времени ![]() . Полная производная
. Полная производная ![]() функции
функции ![]() по
времени определяется формулой:
Ответ:
по
времени определяется формулой:
Ответ: 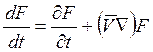 .
.
11. Какое из приведенных ниже высказываний является верным: Ответ: 2) в случае потенциального течения несжимаемой жидкости потенциал скоростей является гармонической функцией.
12. Уравнение неразрывности следует из: Ответ: закона сохранения массы индивидуального объема сплошной среды.
13. Уравнение Эйлера движения идеальной жидкости следует из: Ответ: закона изменения количества движения.
14. Уравнение неразрывности имеет вид:
Ответ: 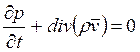 .
.
15. Уравнение Эйлера движения идеальной жидкости имеет вид:
Ответ: 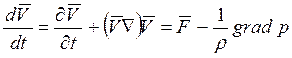 .
.
16. Интеграл Бернулли выводится из: Ответ: 2) дифференциального уравнения движения идеальной жидкости.(уравнения Громеки-Ламба)
17. Какое из условий не требуется при выводе интеграла Коши-Лагранжа: Ответ: требуется: жидкость идеальна, баротропна, движение безвихревое.
18. Произвольная функция времени, входящая в интеграл Коши-Лагранжа: Ответ: 1) Может быть определена, если известны хотя бы в одной точке пространства зависимости от времени потенциала течения, потенциала внешней силы и функции давления.
19. Интеграл Бернулли имеет вид:
Ответ: 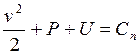 .
.
20. Интеграл Лагранжа-Коши имеет вид:
Ответ: 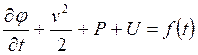 .
.
21. Интеграл Бернулли-Эйлера имеет вид:
Ответ: 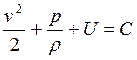 .
.
22. Интеграл Лагранжа-Коши выводится из: Ответ: уравнения Громеки-Ламба.
23. При выводе интеграла Лагранжа-Коши предполагается, что движение жидкости является: Ответ: движение безвихревое, жидкость идеальна, жидкость баротропна.
24. При выводе интеграла Бернулли предполагается, что движение жидкости является: Ответ: движение жидкости стационарно, жидкость идеальна, массовые силы принадлежат к потенциальному силовому полю, жидкость баротропна.
25. В задачах о стационарных потенциальных течениях идеальной несжимаемой жидкости: Ответ: распределение скоростей находится из уравнения Лапласа, а для нахождения распределения давлений используется интеграл Бернулли.
26. ![]() -функция тока,
-функция тока,![]() -
вектор скорости. Справедливы формулы:
Ответ:
-
вектор скорости. Справедливы формулы:
Ответ: ![]() ,
, 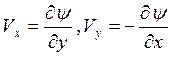 ,
, ![]() .
.
27. Комплексная скорость определяется выражением (![]() -
потенциал скорости,
-
потенциал скорости, ![]() -функция тока):
Ответ:
-функция тока):
Ответ: 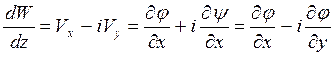 .
.
28. Какой из приведенных ниже комплексных потенциалов соответствует
поступательному течению с постоянной скоростью
Ответ: ![]() :
:![]() . 3)
. 3)![]() .
.
29.
Комплексный потенциал ![]() соответствует
поступательному течению с постоянной скоростью:
Ответ:
соответствует
поступательному течению с постоянной скоростью:
Ответ: ![]() .
.
30.
В задачах обтекания абсолютно твердых тел потоком
идеальной жидкости граничные условия имеют вид:
Ответ: 1) ![]() — нормальная скорость частицы
жидкости.
— нормальная скорость частицы
жидкости.
31. Уравнение Навье-Стокса движения вязкой жидкости следует из: Ответ: уравнения движения сплошной среды в напряжениях или закона изменения количества движения.
32. Уравнение Навье-Стокса движения вязкой жидкости имеет вид:
Ответ: 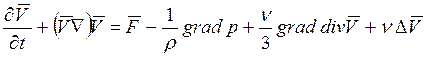 .
.
33. Закон Гука справедлив: Ответ: для малых деформаций.
34. Модуль Юнга определяется выражением:
Ответ: 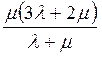 .
.
35. Коэффициент Пуассона определяется выражением:
Ответ: 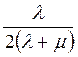 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.