Синтез структуры счетчика и исследование функций счетчика с заданными параметрами. Классификация счетчиков по признакам, страница 2

Один из способов введения обратных связей для получения числа состояний счетчика К < 2^N заключается в обнаружении на выходах разрядов соответствующей кодовой комбинации и последующем сбросе разрядов счетчика в исходное состояние. В этом случае счет всегда начинается с исходного состояния, поэтому состояния разрядов счетчика в двоичном коде соответствуют числу поданных на вход импульсов. Как стоятся такие счетчики рассмотрим  позже.

Применив логические элементы (например, типа И-ИЛИ-НЕ), на Т-входах триггеров можно построить реверсивный счетчик. Такой счетчик может осуществлять как прямой, так и обратный счет (рис.3).

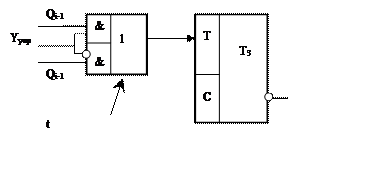
Рис.3. Разряд реверсивного счетчика

Двоичные  счетчики с

параллельным и  сквозным  переносом 

Во многих важных для практики случаях быстродействие асинхронных счетчиков с последовательным переносом оказывается недостаточным. Для ускорения процесса счета необходимо, чтобы изменение состояний отдельных разрядов происходило сразу после прихода очередного счетного импульса в нескольких разрядах. Найдем логические уравнения состояний отдельных разрядов трехразрядного счетчика, учитывающие состояния более младших разрядов. Для этого построим таблицу истинности для случая применения Т-триггеров в режиме суммирования (табл.1), а затем с использованием диаграмм Вейча-Карно определим функции возбуждения входов триггеров.

Таблица 1

t			t+1			входы
Q1	Q2	Q3	Q3	Q2	Q1	T3	T2	T1
0	0	0	0	0	1	0	0	1
0	0	1	0	1	0	0	1	1
0	1	0	0	1	1	0	0	1
0	1	1	1	0	0	1	1	1
1	0	0	1	0	1	0	0	1
1	0	1	1	1	0	0	1	1
1	1	0	1	1	1	0	0	1
1	1	1	0	0	0	1	1	1

Из диаграмм получим:

                                                                    (1)

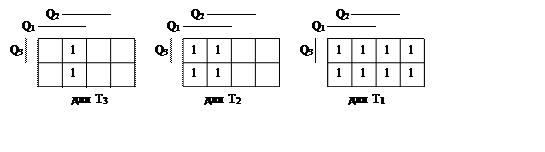
или

                                                                   (2)

Формулы 1 и 2 для n-го триггера имеют вид

                                                   - (3)

определяет построение схемы для параллельногопереноса  с учетом  Т2 и Т1,

-                                                (4)

определяет построение схемы для сквозного переноса  с учетом  Т2 и Т1.

Для вычитающего счетчика формулы имеют вид

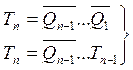                                                 (5)

Если ввести сигналы управления Yпр и Yобр , то получим формулы для реверсивных счетчиков параллельного и сквозного переносов

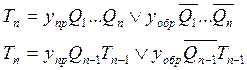Рассмотрим построение счетчиков с параллельным переносом. Счетчик функционирует согласно выражению (3) (рис.4).

Рис.4. Счетчик с параллельным переносом

Число входов в схемах одновременного переноса (логических элементах И) равно номеру разряда счетчика, для которого этот перенос формируется. Сигнал переноса в каждый разряд счетчика проходит только через один логический элемент И, поэтому данный счетчик является самым быстродействующим из рассмотренных. Минимальный период следования счетных импульсов Тпп в данной схеме устанавливается из условия Тпп ³ tп + tпп +