Файл M-9
Лекция № __Методы вероятностного описания погрешностей
результатов прямых измерений.
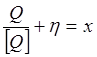 |
Это уравнение выражает некоторое действие, процедуру сравнения в реальных условиях, которая и является измерением. Главной особенностью измерительной процедуры является то, что при ее повторении из-за случайного характера η отсчет х по шкале отношений получается все время разным. Слагаемое η, являющееся случайным, не может быть известно в принципе. Это закон природы. Поэтому определить истинное значение измеряемой ФВ невозможно. На основании опыта практических измерений может быть сформулировано утверждение, называемое основным постулатом метрологии:
отсчет является случайным числом.
На этом постулате основана вся метрология. Это уравнение является математической моделью измерения по шкале отношений. Отсчет в ней не может быть представлен одним числом. Его можно лишь описать словами или математическими символами, представить массивом экспериментальных данных, таблично, графически или аналитическим выражением.
Для характеристики частоты появления различных значений случайной величины х (случайных погрешностей D) теория вероятностей предлагает пользоваться законом распределения вероятностей различных значений этой величины.
Теория погрешностей основывается на аналогии между появлением случайных погрешностей при многократно повторяемых измерениях и совершением случайных событий.
Случайным наз. такое событие, которое при осуществлении определенного комплекса условий может произойти или не произойти. Сумма случайных изменений, появляющихся при каждом измерении, может быть любой как по размеру, так и по знаку. Эту сумму мы наз. случайной погрешностью измерения. Вероятность события является количественной оценкой объективной возможности появления этого события. Вероятность достоверного события = 1, вероятность невозможного события = 0.
Теоретическое определение вероятности в общем виде Р(А)=р, т.е. вероятность события А равна р. Если известно, что из общего числа событий n появление желательного результата возможно m раз, то Р(А) = m/n. Но теоретическое определение вероятности не всегда возможно. В этих случаях применяют статистический метод определения вероятности события, в частности случайной погрешности измерения.
В основе теории погрешностей лежат два предположения, подтверждаемых опытом.
1. При большом числе измерений случайные погрешности одинаковой величины, но разного знака, встречаются одинаково часто.
2. Большие (по абсолютной величине) погрешности встречаются реже, чем малые, т.е. вероятность появления погрешности уменьшается с ростом величины погрешности.
Допустим, что мы произвели n прямых измерений некоторой ФВ, истинное значение которой (нам неизвестное) обозначим через а. Обозначим через а1,а2,…, аn результаты отдельных измерений, а через
Dai* = a - ai
- истинную абсолютную погрешность i-го измерения.
Тогда результаты измерений можно представить в виде
a1 = а - Dа1*
а2 = а - Dа2* (1)
…………..
аn = а - Dаn*
Естественно, что абсолютные погрешности Dа1*, Dа2*,…., Dаn* могут принимать как положительные, так и отрицательные значения.
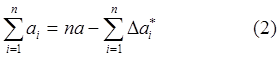 |
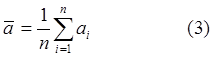 |
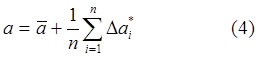 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.