





















Дальневосточный государственный технический университет
(ДВПИ им. В.В. Куйбышева)
Кафедра механики деформируемого твердого тела
Курсовая работа
по механике деформируемого твёрдого тела
Группа: E-8531
Выполнил:
Проверил:
Владивосток 2011 г.
Задание на курсовую работу
По исходным данным необходимо:
1. а) Тензор деформации Грина, деформации Коши, вращение Коши. б) Изменение длины линейных элементов локального базиса. в) Изменение направления вектора локального базиса.
г) Изменение углов между векторами локального базиса. д) Главные компоненты тензора деформации Коши и главные оси деформации (построить). е) Инварианты тензора деформации Грина.
ж) Объёмную деформацию.
з) Шаровой тензор и девиатор тензора деформаций.
и) Интенсивность линейных деформаций, интенсивность деформаций сдвига, октаэдрическую деформацию сдвига.
к) Скорость деформаций, интенсивность скоростей деформаций.
л) Проверить условия сплошности.
2. а) Главные напряжения, направление главных осей тензора напряжений.
б) Экстремальные касательные напряжения. Построить площадки, на которых действуют максимальные касательные напряжения. в) Октаэдрические касательные напряжения. г) Шаровой тензор и девиатор тензора напряжений. д) Интенсивность напряжений, интенсивность касательных напряжений. е) Для площадки заданной направляющим вектором найти компоненты полного напряжения, величины нормального и касательного напряжений, угол между напряжением и нормалью к площадке.
Исходные данные
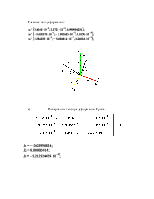
1. Задано поле перемещений в лагранжевой системе координат, являющейся в начальный момент декартовой прямоугольной в точке Р (0,3;0,1;0,4) в момент времени t=1:
U1=(1-x12-x22-x32)e-7-t;
U2=0,5*(1-x22-x32)e-7-t;
U3=(1 -x32)e-2-t;
2. Дан тензор напряжений и направляющий вектор:

![]()
1. а) Тензор деформации Грина, деформации Коши, вращение Коши.
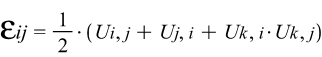 - формула
тензора деформаций Грина
- формула
тензора деформаций Грина
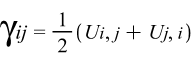 -
формула тензора деформаций Коши
-
формула тензора деформаций Коши
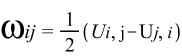 -
формула тензора вращений Коши
-
формула тензора вращений Коши
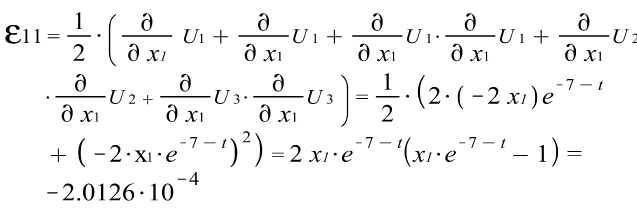
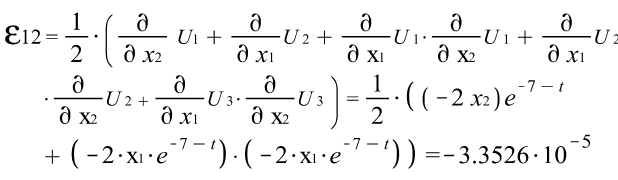
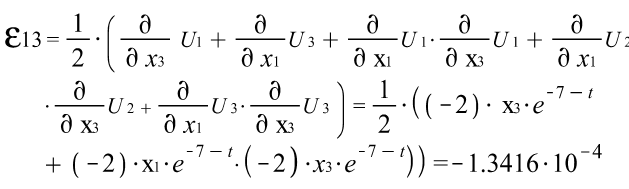
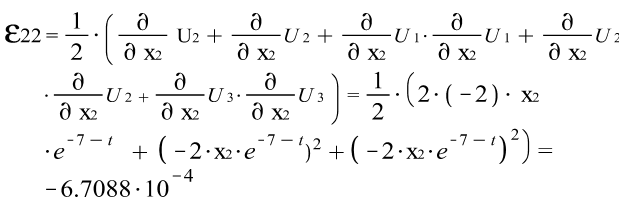
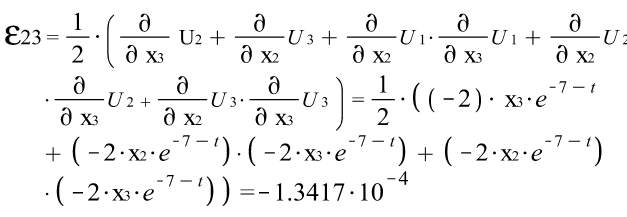
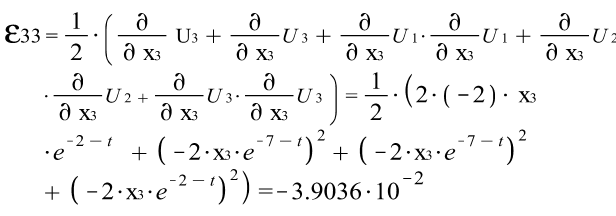
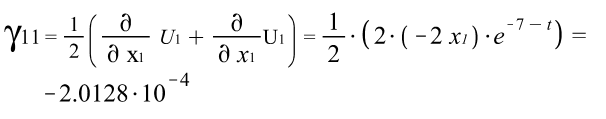
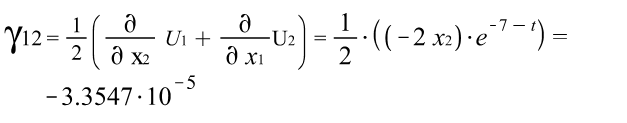
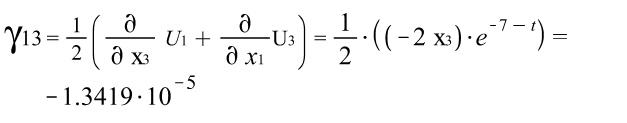
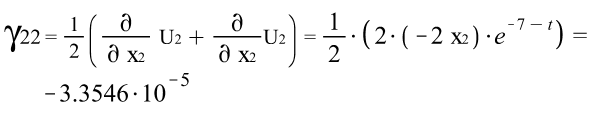
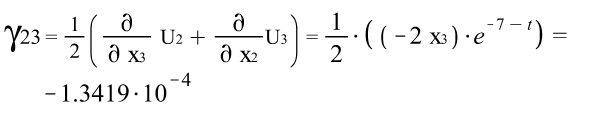
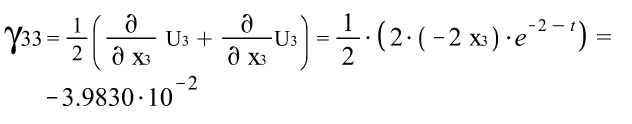
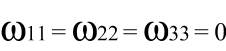
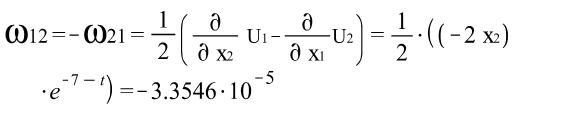
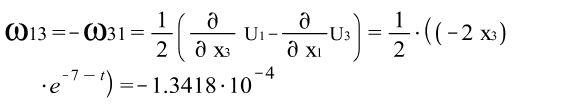

Тензора деформаций Коши:
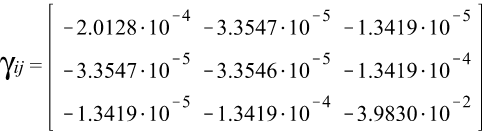
Тензора вращений Коши:

Тензора деформаций Грина:
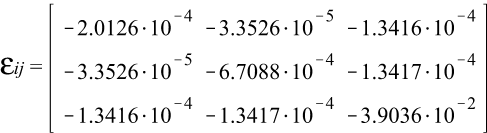
б) Изменение длины линейных элементов локального базиса:
![]()
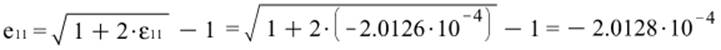
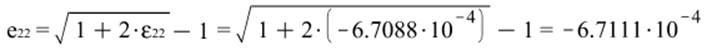
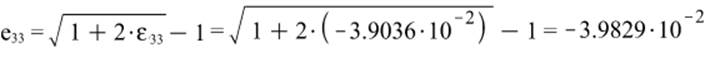
в) Направляющие косинусы после деформации:
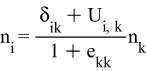
Х1: 
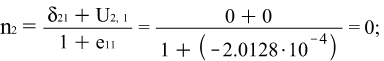
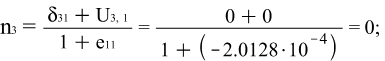
Х2: 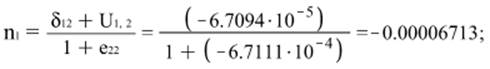
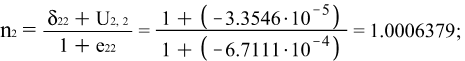
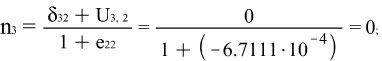
Х3: 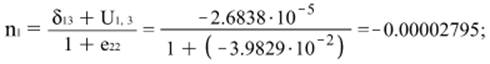

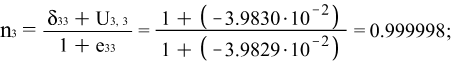
г) Углы определяющие
деформацию сдвига в координатных плоскостях: 
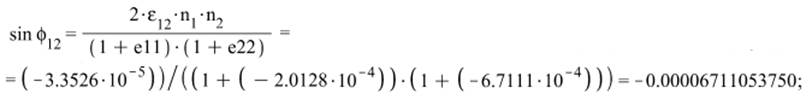
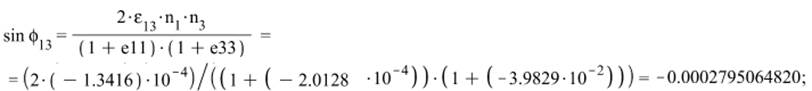

![]()
![]()
![]()
д) Главные компоненты тензора деформации Коши и главные оси деформации:
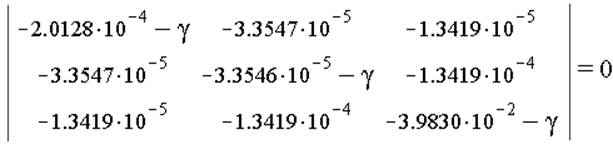
![]()
Решая уравнение, найдём главные компоненты тензора деформации Коши:
![]()
![]()
![]()
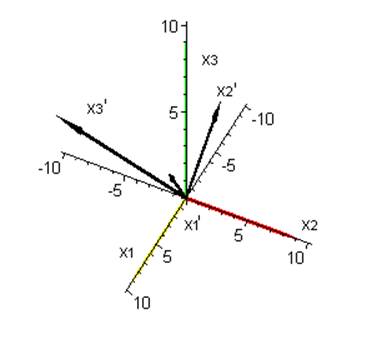
Главные оси деформации:
При ![]()
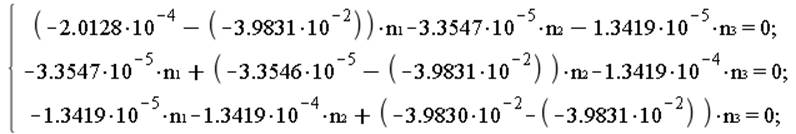
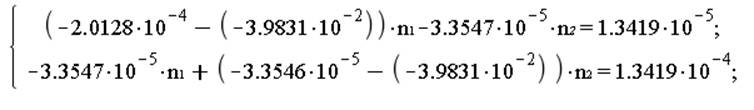
![]()
![]()
![]()


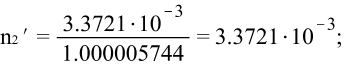
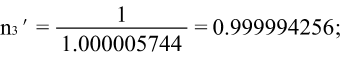
При ![]()
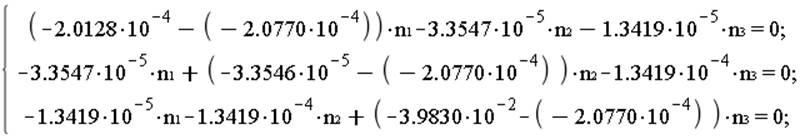
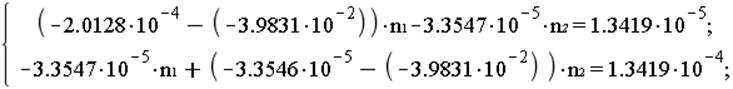
![]()
![]()
![]()

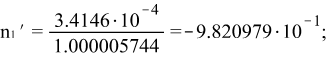
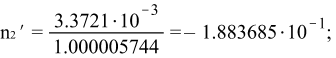
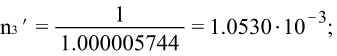
При ![]()
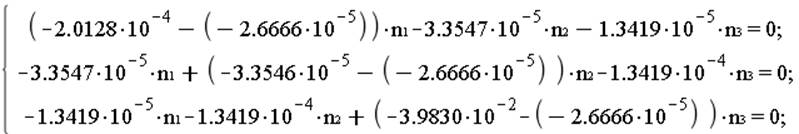
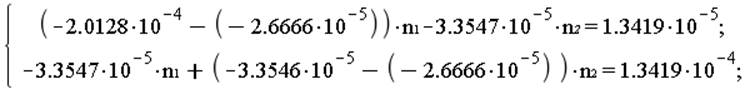
![]()
![]()
![]()
![]()
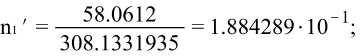
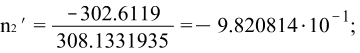
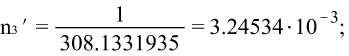
Главные оси деформации:
![]()
![]()
![]()
е) Инварианты тензора деформации Грина.
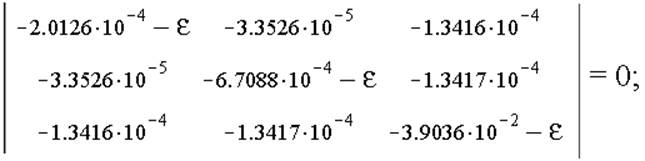
![]()
![]()
![]()
ж) Объёмная деформация:
![]()

з) Шаровой тензор и девиатор тензора деформаций:
![]()
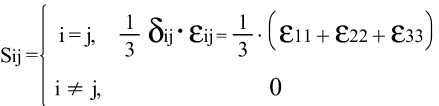
Шаровой тензор:

![]()
Девиатор:
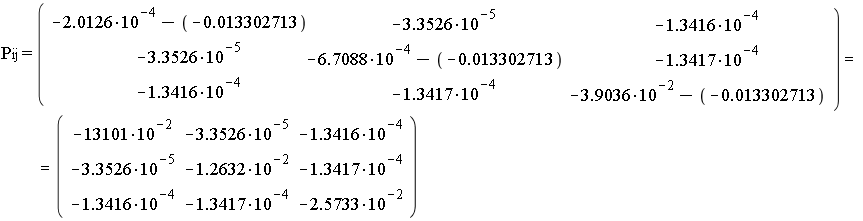
и) Интенсивность линейных деформаций, интенсивность деформаций сдвига, октаэдрическую деформацию сдвига.
Интенсивность линейной деформации:
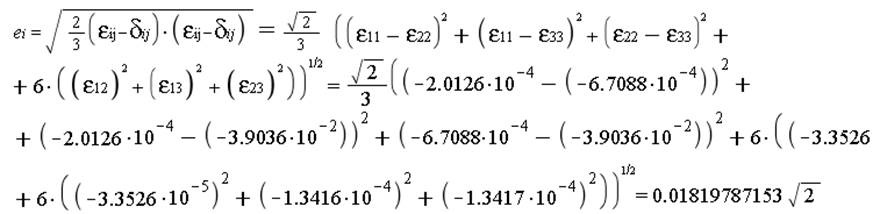
Интенсивность деформаций сдвига:
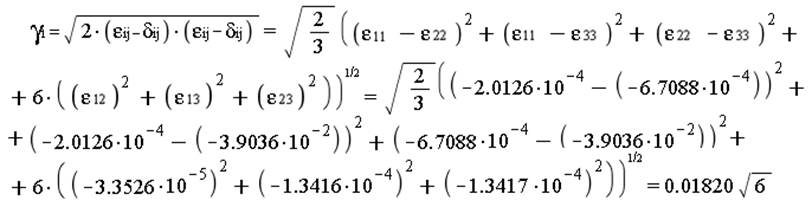
Октаэдрическая деформация сдвига:
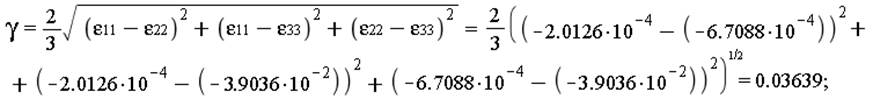
к) Скорость деформаций, интенсивность скоростей деформаций.

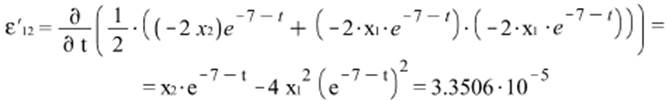
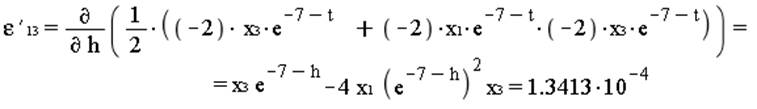
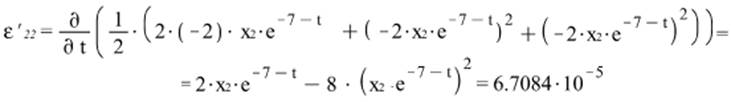
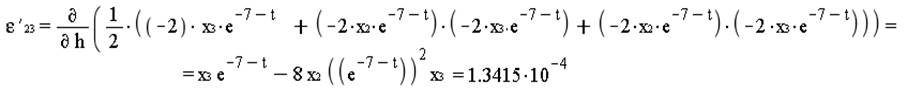
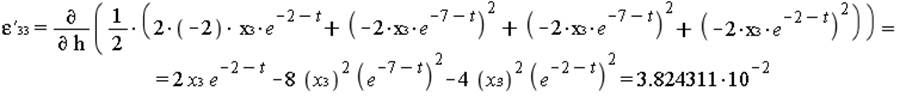
Cкорость деформации:

Интенсивность скоростей деформаций:
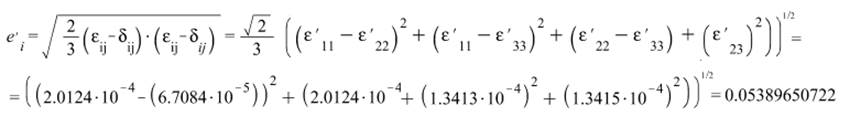
л) Условия сплошности.
![]()
1)
![]()
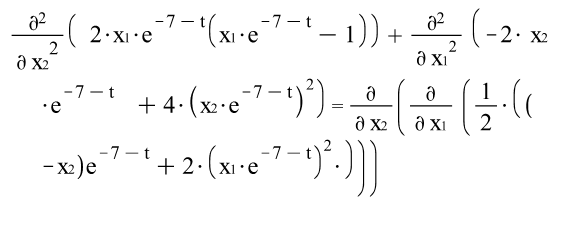
![]()
![]()
2)
![]()
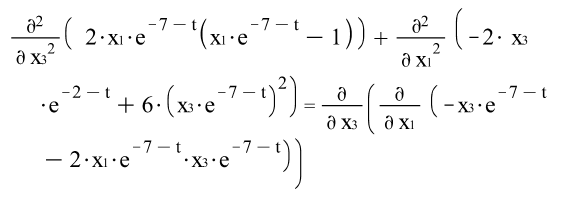
![]()
0=-2.2507*![]()
-2.2507*![]()
3) 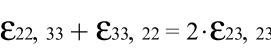
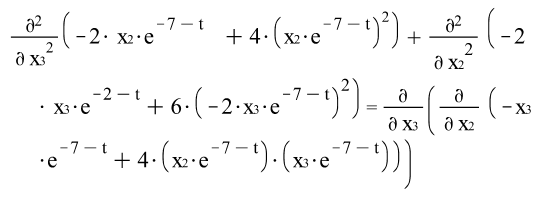
![]()
![]()
![]()
4) ![]()
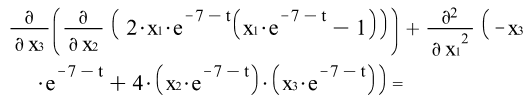
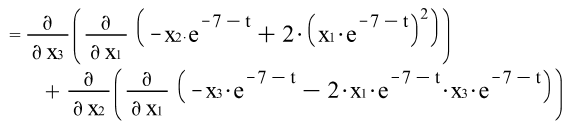
![]()
5) ![]()
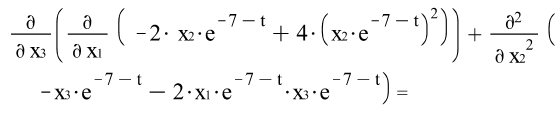
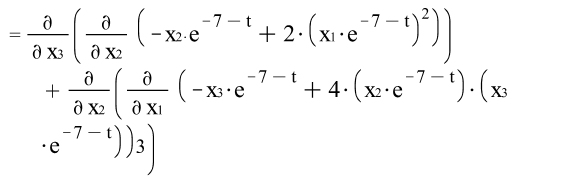
![]()
6) ![]()
![]()

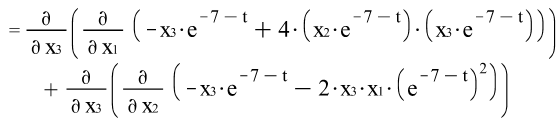
![]()
ð условия сплошности выполняются.
1. а) Главные напряжения, направление главных осей тензора напряжений.
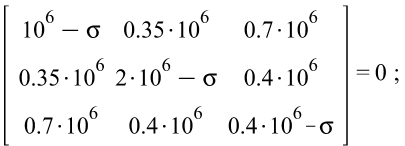
![]()
Решая уравнение, найдём главные напряжения:
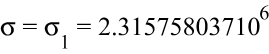
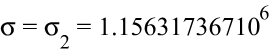
![]()
Направление главных осей тензора напряжений:
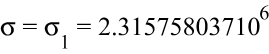
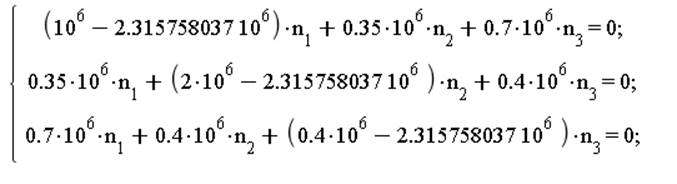
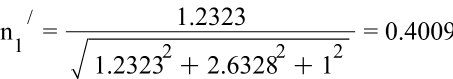
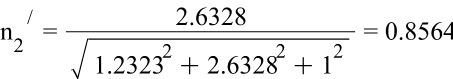
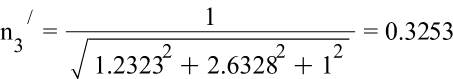
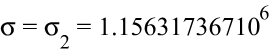
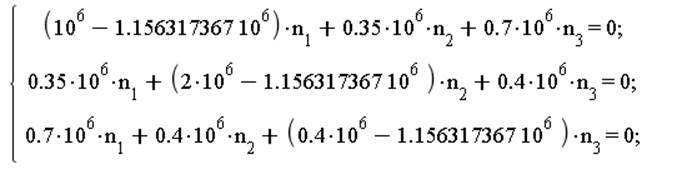
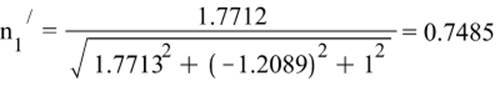
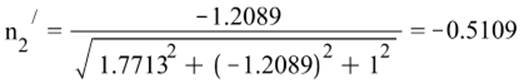
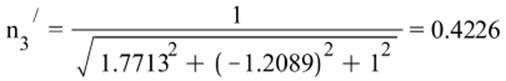
![]()
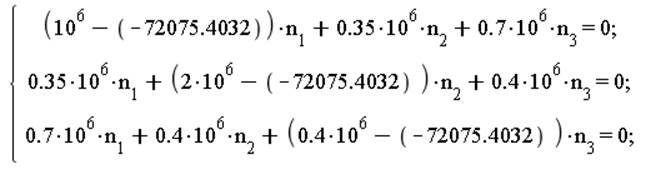
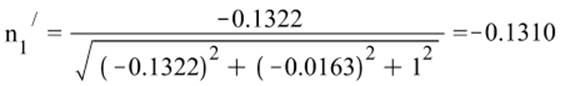
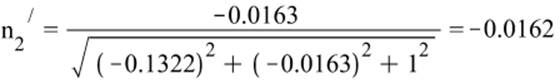
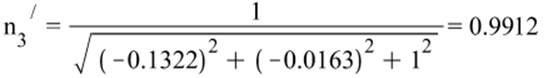
Направление главных осей тензора напряжений:
![]()
![]()
![]()
б) Экстремальные касательные напряжения. Построить площадки, на которых действуют максимальные касательные напряжения.
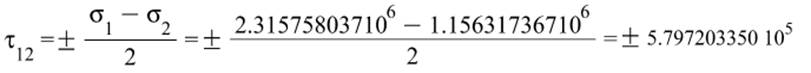
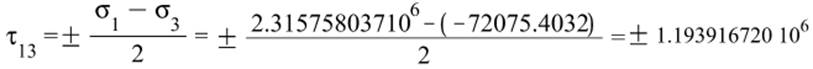
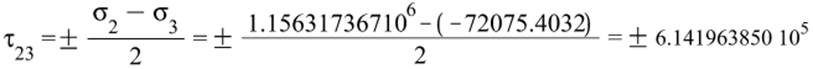
![]()
![]()
![]()
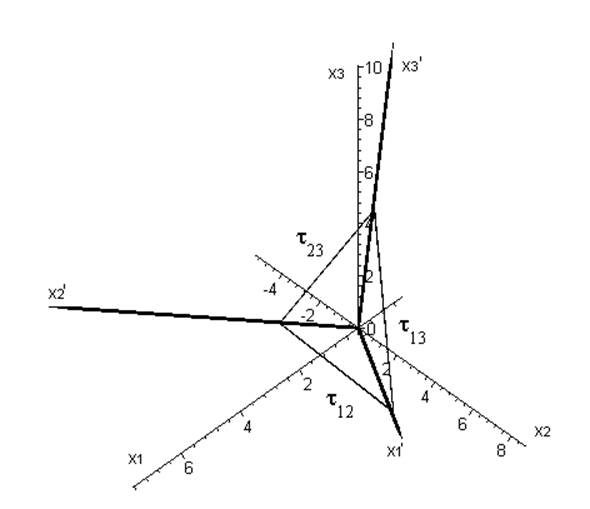
в) Октаэдрические касательные напряжения.
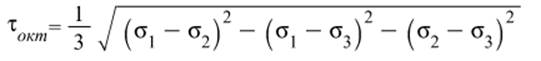

г) Шаровой тензор и девиатор тензора напряжений.
Шаровой тензор:
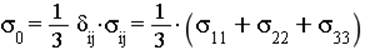
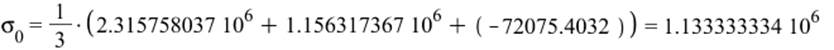
Девиатор:


д) Интенсивность напряжений, интенсивность касательных напряжений.
Интенсивность напряжений:
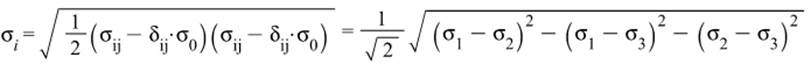

Интенсивность касательных напряжений:

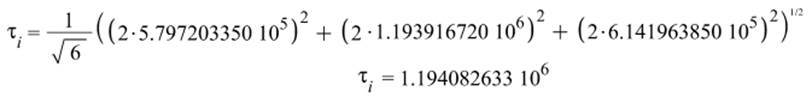
е)
Для площадки заданной направляющим вектором ![]() найти компоненты полного
напряжения, величины нормального и касательного напряжений, угол между
напряжением и нормалью к площадке.
найти компоненты полного
напряжения, величины нормального и касательного напряжений, угол между
напряжением и нормалью к площадке.

![]()
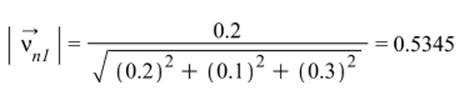
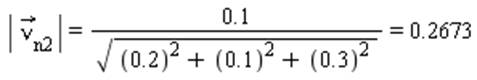
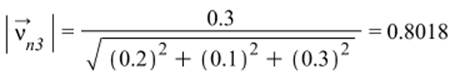
![]()
Нормальное напряжение:

Полное напряжение:
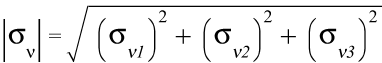
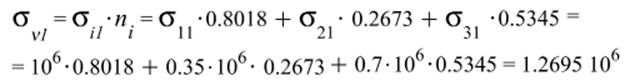
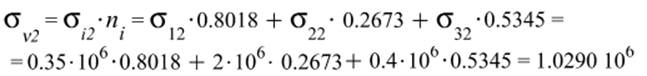
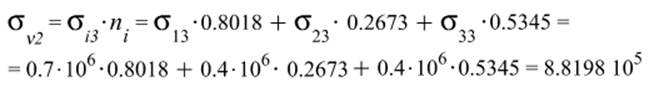
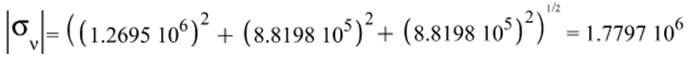
Касательное напряжение:

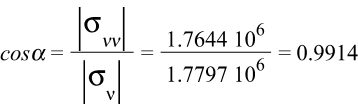
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.