частота вращения шестерни, об/с; Т3 –
вращающий момент на валу колеса, Н×м;
![]() -
коэффициент учитывающий вид термообработки
-
коэффициент учитывающий вид термообработки ![]() =13
– для прямозубых передач[1]
=13
– для прямозубых передач[1]
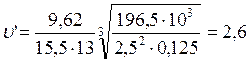 м/с,
м/с,
Для данной скорости рекомендуется 9-я степень точность.
Вычисляем межосевое расстояние по формуле (17)
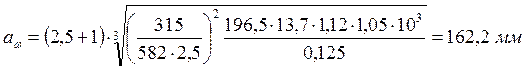
Принимаем
![]() по ГОСТ 2185.
по ГОСТ 2185.
Определяем рабочую ширину венца
![]() ,
(20)
,
(20)
![]() .
.
Принимаем ширину венца ![]() и
и ![]() .
.
Модуль зацепления mn, мм [1]:
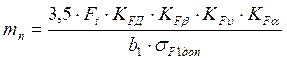 ,
(21)
,
(21)
где Ft –окружная сила в зацеплении, Н,
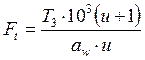 ,
(22)
,
(22)
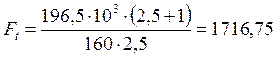 Н.
Н.
![]() –
коэффициент долговечности, принимаем
–
коэффициент долговечности, принимаем ![]() =1[1]
=1[1]
![]() -
коэффициент концентрации нагрузки.
-
коэффициент концентрации нагрузки.
Коэффициент ![]() принимаем
в зависимости от параметра
принимаем
в зависимости от параметра ![]()
![]() [1]
[1]
![]() -
коэффициент динамичности.
-
коэффициент динамичности.
Коэффициент ![]() принимаем
в зависимости от параметра
принимаем
в зависимости от параметра ![]()
![]() [1]
[1]
![]() -
коэффициент, учитывающий неравномерность распределения нагрузки между зубьями при
расчете прямозубых передач значение
-
коэффициент, учитывающий неравномерность распределения нагрузки между зубьями при
расчете прямозубых передач значение ![]() .
.
Вычисляем модуль зацепления по формуле (21)
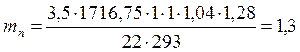 мм,
мм,
Полученное значение модуля округляется до ближайшего стандартного в соответствии с предпочтительным рядом модулей [1].
Принимаем ![]() по
ГОСТ 9563.
по
ГОСТ 9563.
Определяем число зубьев шестерни и колеса:
![]() , (23)
, (23)
где ![]() -
предварительный угол наклона линии зуба в прямозубых передачах
-
предварительный угол наклона линии зуба в прямозубых передачах ![]() =0
=0
![]() ;
;
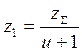 , (24)
, (24)
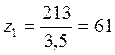 .
.
![]() , (25)
, (25)
![]() .
.
Принимаем ![]() и
и ![]() мм.
мм.
Фактическое передаточное число
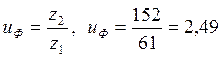 . (25)
. (25)
Отклонение фактического (уточненного) передаточного числа от ранее принятого
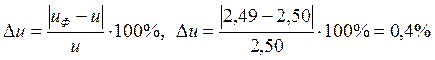 ; (27)
; (27)
0,4%<2,5%.
Вычисляем делительные диаметры, диаметры вершин, основные диаметры и диаметры впадин шестерни и колеса
![]() ; (28)
; (28)
![]() ; (29)
; (29)
![]() ; (30)
; (30)
![]() ;
;
![]() ;
;
![]() .
.
Уточняем межосевое расстояние
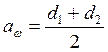 , (31)
, (31)
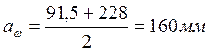 .
.
Окружная сила по формуле (22).
Радиальная сила Fr, Н [1]:
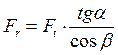 , (32)
, (32)
где a - угол зацепления, град a=20°,
b - угол подъема линии зуба, град b = 0 для прямозубой передачи,
![]() Н.
Н.
Определяем действительное контактное напряжение
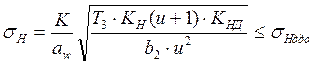 , (33)
, (33)
где ![]() -
коэффициенты нагрузки.
-
коэффициенты нагрузки.
Допускается ![]() не
более 10…15% (недогрузка передачи) и
не
более 10…15% (недогрузка передачи) и ![]() не
более 3…5% (перегрузка).
не
более 3…5% (перегрузка).
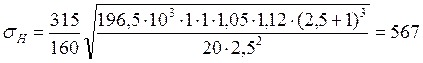 МПа<
МПа<![]() =
582 МПа.
=
582 МПа.
Разница между фактическим и допускаемым напряжением
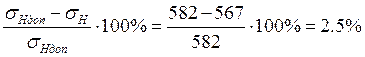 . (34)
. (34)
Результат считается хорошим, так как нагрузка передачи 2.5 %, что меньше 10…15% допускаемой.
Определяем действительные напряжения изгиба шестерни![]() и
колеса
и
колеса![]()
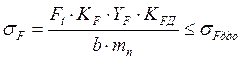 , (35)
, (35)
где ![]() -
коэффициент нагрузки.
-
коэффициент нагрузки.
![]() -
коэффициент формы зуб, принимают в зависимости от эквивалентного числа зубьев
-
коэффициент формы зуб, принимают в зависимости от эквивалентного числа зубьев ![]() [1]
[1]
- для прямозубых колес
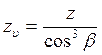 , (36)
, (36)
где b - угол подъема линии зуба, град b = 0 для прямозубой передачи.
Определяем эквивалентное число зубьев
![]() ;
; ![]() ; (37)
; (37)
![]() ;
;![]() (38)
(38)
Определяем
действительные напряжения изгиба шестерни![]()
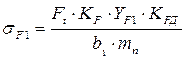 , (39)
, (39)
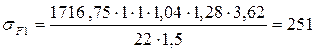 МПа<
МПа<![]() =293МПа.
=293МПа.
Определяем
действительные напряжения изгиба колеса![]()
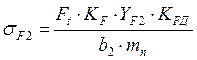 , (40)
, (40)
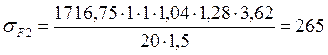 МПа<
МПа<Исходные данные:
– крутящий момент на валу колеса, Т2, Н×м 64,2;
– передаточное отношение, u 3,15;
– частота вращения быстроходного вала, n1, об/с 11,93
– допускаемое контактное напряжение,![]() ,
МПа 582;
,
МПа 582;
– допускаемое напряжение изгиба, ![]() ,
МПа 293;
,
МПа 293;
– допускаемое напряжение изгиба, ![]() ,
МПа 255;
,
МПа 255;
Ориентировочное значение межосевого расстояния ![]() ,
мм.
,
мм.
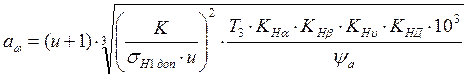
где ![]() –
вспомогательный коэффициент
–
вспомогательный коэффициент ![]() -
для косозубых колес;
-
для косозубых колес;
![]() –
коэффициент, учитывающий неравномерность распределения нагрузки Между зубьями
–
коэффициент, учитывающий неравномерность распределения нагрузки Между зубьями ![]() -
для косозубых колес ;
-
для косозубых колес ;
![]() -
коэффициент концентрации нагрузки на контактную выносливость. Коэффициент
-
коэффициент концентрации нагрузки на контактную выносливость. Коэффициент ![]() принимаем
в зависимости от параметра
принимаем
в зависимости от параметра ![]()
![]() [1]
[1]
Определяем
коэффициент ![]()
![]() –
коэффициент ширины зубчатого колеса
–
коэффициент ширины зубчатого колеса ![]() -
для косозубых колес.
-
для косозубых колес.
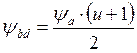 ,
,
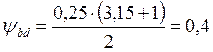 .
.
![]() -
коэффициент динамичности
-
коэффициент динамичности ![]() Коэффициент
Коэффициент
![]() принимаем
в зависимости от параметра
принимаем
в зависимости от параметра ![]() [1]
[1]
Вычисляем предварительную окружную скорость
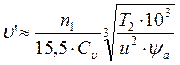 ,
,
где n2 – частота вращения шестерни, об/с; Т3 –
вращающий момент на валу колеса, Н×м;
![]() -
коэффициент учитывающий вид термообработки
-
коэффициент учитывающий вид термообработки ![]() =15
– для косозубых передач[1]
=15
– для косозубых передач[1]
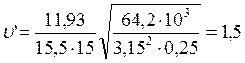 м/с.
м/с.
Для данной скорости рекомендуется 9-я степень точность.
Так как редуктор
соосный то принимаем ![]() =160 мм, смотрим пункт 2
=160 мм, смотрим пункт 2
![]()
![]() .
.
Принимаем ширину венца ![]() и
и ![]() .
.
Модуль зацепления mn, мм [1]:
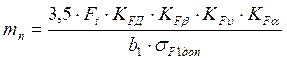 ,
,
где Ft –окружная сила в зацеплении, Н,
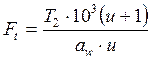 ,
,
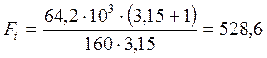 Н.
Н.
![]() –
коэффициент долговечности, принимаем
–
коэффициент долговечности, принимаем ![]() =1[2]
=1[2]
![]() -
коэффициент концентрации нагрузки.
-
коэффициент концентрации нагрузки.
Коэффициент ![]() принимаем
в зависимости от параметра
принимаем
в зависимости от параметра ![]()
![]() [2]
[2]
![]() -
коэффициент динамичности.
-
коэффициент динамичности.
Коэффициент ![]() принимаем
в зависимости от параметра
принимаем
в зависимости от параметра ![]()
![]() [2]
[2]
![]() -
коэффициент, учитывающий неравномерность распределения нагрузки между зубьями
при расчете прямозубых передач значение
-
коэффициент, учитывающий неравномерность распределения нагрузки между зубьями
при расчете прямозубых передач значение ![]() .
.
Вычисляем модуль зацепления по формуле (21)
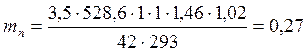 мм,
мм,
Полученное значение модуля округляется до ближайшего стандартного в соответствии с предпочтительным рядом модулей [1].
Принимаем ![]() по
ГОСТ 9563.
по
ГОСТ 9563.
Определяем предварительный минимальный угол подъема линии зуба, град,
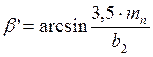 , (41)
, (41)
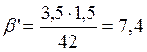 °.
°.
Определяем число зубьев шестерни и колеса:
![]() , (42)
, (42)
где ![]() -
предварительный угол наклона линии зуба
-
предварительный угол наклона линии зуба
![]() .
.
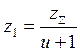 ,
,
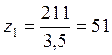 .
.
![]() ,
,
![]() .
.
Принимаем ![]() и
и ![]() мм.
мм.
Фактическое передаточное число
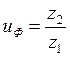 ,
,
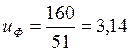 .
.
Отклонение фактического (уточненного) передаточного числа от ранее принятого
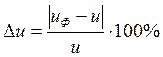 ,
,
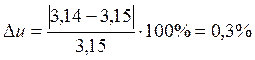 .
.
0,3%<2,5%.
Уточняем угол наклона линии наклона зуба b, град,
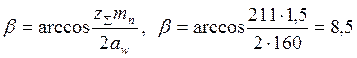 °. (43)
°. (43)
Вычисляем делительные диаметры, диаметры вершин, основные диаметры и диаметры впадин шестерни и колеса
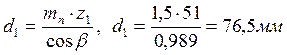 ; (44)
; (44)
![]() ;
;
![]() ;
;
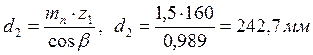 ;
;
![]() ;
;
![]() .
.
Уточняем межосевое расстояние
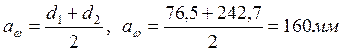 .
.
Окружная сила по формуле (22).
Осевая сила Fa, Н [1]:
Fa = Ft×tgb=528,6×0,149=79 Н, (45)
Радиальная сила Fr, Н [1]:
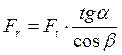 ,
,
где a - угол зацепления, град a=20°
b - угол подъема линии зуба, град.
![]() Н,
Н,
Определяем действительное контактное напряжение
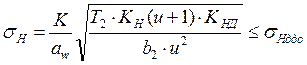 ,
,
где ![]() -
коэффициенты нагрузки.
-
коэффициенты нагрузки.
Допускается ![]() не
более 10…15% (недогрузка передачи) и
не
более 10…15% (недогрузка передачи) и ![]() не
более 3…5% (перегрузка).
не
более 3…5% (перегрузка).
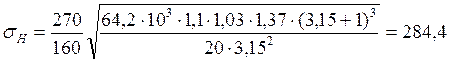 МПа<
МПа<![]() =
582 МПа.
=
582 МПа.
Так как редуктор соосный, то недогрузка вполне вероятна.
Определяем действительные напряжения изгиба
шестерни![]() и
колеса
и
колеса![]()
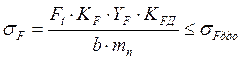 ,
,
где ![]() -
коэффициент нагрузки.
-
коэффициент нагрузки.
![]() -
коэффициент формы зуб, принимают в зависимости от эквивалентного числа зубьев
-
коэффициент формы зуб, принимают в зависимости от эквивалентного числа зубьев ![]() [1]
[1]
- для прямозубых колес
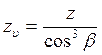 , (46)
, (46)
где b - угол подъема линии зуба, град.
Определяем эквивалентное число зубьев
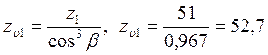 ;
; ![]() ;
;
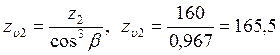 ;
;![]() .
.
Определяем
действительные напряжения изгиба шестерни![]()
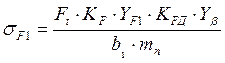
где
![]() -
коэффициент наклона зуба,
-
коэффициент наклона зуба,
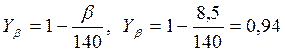
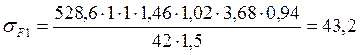 МПа<
МПа<![]() =293МПа.
=293МПа.
Определяем
действительные напряжения изгиба колеса![]()
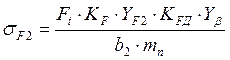 ,
,
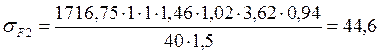 МПа<
МПа<![]() =255МПа.
=255МПа.
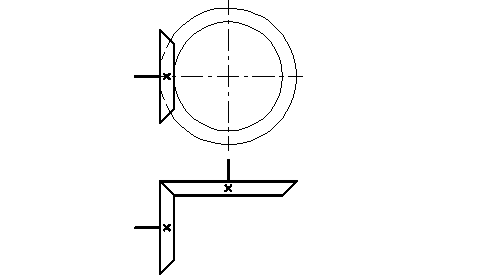
Рисунок 2 - Кинематическая схема конической передачи.
Исходные данные:
– крутящий момент на валу колеса, Т4, Н×м 456,8;
– передаточное отношение, u 2;
– частота вращения вала III, n3, об/с 3,05,
– допускаемое контактное напряжение,![]() ,
МПа 582;
,
МПа 582;
– допускаемое напряжение изгиба, ![]() ,
МПа 293;
,
МПа 293;
– допускаемое напряжение изгиба, ![]() ,
МПа 255.
,
МПа 255.
Определяем предварительное значение окружной скорости
Вычисляем предварительную окружную скорость
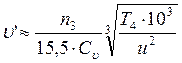 ,
,
где n3 – частота вращения шестерни, об/с; Т4 –
вращающий момент на валу колеса, Н×м;
![]() -
коэффициент учитывающий вид термообработки
-
коэффициент учитывающий вид термообработки ![]() =10
– для конических передач[1]
=10
– для конических передач[1]
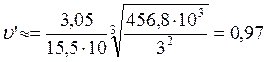 м/с.
м/с.
Внешний делительный диаметр колеса de2, мм [5]:
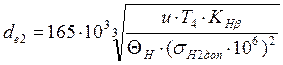 ,
(48)
,
(48)
где Т3 – вращающий момент на валу колеса, Н×м (Т2 = 456,8 Н×м);
u – передаточное отношение конической передачи (u = 4);
![]() = 1,85 – при твердости колеса и шестерни
менее или равно 350НВ[1];
= 1,85 – при твердости колеса и шестерни
менее или равно 350НВ[1];
KHb – коэффициент вида конических колес KHb = 1,1 для колес
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.