Консольные краны. Металлоконструкция крана. Крюковая подвеска. Составление конструктивной схемы крана, страница 3

Согласно расчетной схеме сосредоточенный вес в узлах:

G₇= 1/2х(G_7-6+G_7-5),                                                         (14)

G₇= 76,5Н

G₆= 1/2х(G_7-6+G_6-4+G_5-6),                                                     (15)

G₆= 81,5 Н

G₅=1/2х( G_7-5+G_5-4+G_5-3+G_5-3),                                              (16)

G₅=36,3  Н

G₄=1/( G_6-4+G_3-4+G_1-4+G_2-4+G_4-5),                                              (17)

G₄=281Н

     G₃=1/2х(G_5-3+G_3-4),                                             (18)

G₃= 17,7Н

G₂=1/2х( G_2-4 ),                                                        (19)

G₂= 1,0 Н

G₁= G_1-4 /2,                                                        (19)

G₁= 5,4 Н

5.2 Определим координату “x” центра тяжести МК.

xG=G_ix_i,                                                      (20)

G=252 Н

x=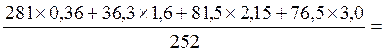1,2 м

   5.3 Определим реакции в узлах 1и3 от собственного веса.

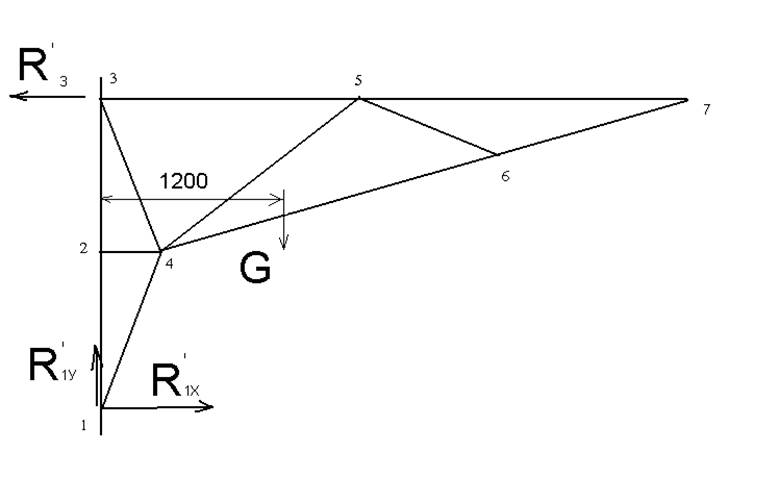
Рисунок 5.1.

Из Σm₁=0:

R₃х2-Gх1,4=0

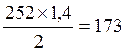R₃^’= Н

ΣF_x=0:

R_1Y-G=0

R_1Y=252Н

R_1х- R₃=0

R_1х- R₃=91,2Н

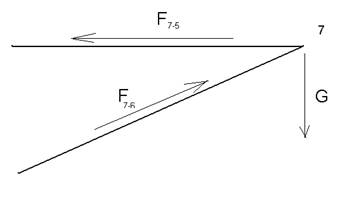
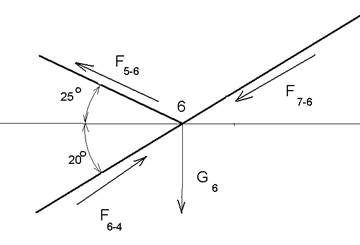
Узел 7:

ΣF_х = 0;

-F^‘_7-6хcos 14⁰- F^‘_7-5 = 0;

F^‘_7-5= F^‘_7-6cos 14⁰;

Рисунок 5.2-реакции в узле №7.

 

ΣF_у = 0;

F_7-6 хsin 14⁰ –G₇=0

F_7-5= F_7-6 хsin 14⁰

ΣF_y=0;

F_7-6 хsin 14⁰ –G₇=0

F_7-6 =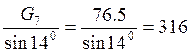Н

F_7-5 =316хсоs 14⁰=307

Узел 6:

ΣF_х = 0;

(F_6-4+F_5-6-F_7-6)хcos 14⁰=0

F_5-6= F_6-4- F_7-6

ΣF_y = 0;

(F_6-4+F_5-6-F_7-6)хsin 14⁰-G₆=0

F_6-4= F_7-6-( F_6-4- F_7-6)+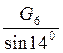

F_6-4=512Н                                                     Рисунок 5.3- реакции в узле №6.

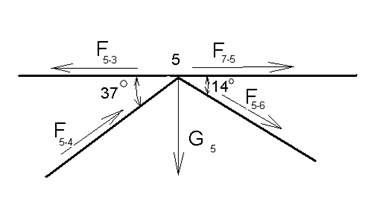
Узел 5:

ΣF_у = 0

-F^‘_5-4х sin 37⁰-F^‘_5-6х sin 37⁰ -G₅  = 0;

F_5-4=116 Н

ΣF_х = 0;                                  

Рисунок 5.4- реакции в узле №5.

ΣF_7-5 = F^‘_5-3 – F^‘_5-6  cos 37⁰⁺ F^‘_5-4 хcos 37⁰=0

F_3-5=560 Н

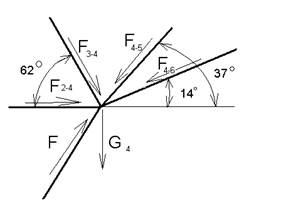Узел 4:

ΣF_х = 0;

-F^‘_4-6=F^‘_4-2- F^‘_4-5cos 37⁰- F^‘_4-3cos 62⁰-G₄

sin 20⁰= 0;

ΣF_у = 0;

ΣF_у = -F^‘_4-5 sin 37⁰+ F^‘_4-3 sin62⁰-G₄

cos 20⁰=0                                                      Рисунок 5.6- реакции в узле №4.

F^‘_4-3= (F^‘_4-5 sin 37⁰+G₄ cos 20⁰)/ sin 62⁰

F^‘_4-3=120,5 Н

F^‘_4-2=F^‘_4-6+F^‘_4-5cos 37⁰+ F^‘_4-3cos 62⁰+G₄ sin 20⁰

F^‘_4-2=56 Н

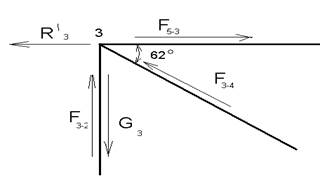Узел 3:

ΣF_х = 0;

-F^‘_3-5-F^‘_3-1- F^‘_3-4cos 62⁰-G₃ sin 38⁰= 0;

ΣF_у = 0;

ΣF_у = F^‘_3-2- F^‘_3-4 sin38⁰-G₃  cos 38⁰=0

F^‘_3-2= F^‘_3-4 sin 38⁰+G₃ cos 38⁰                                Рисунок 5.7- реакции в узле №3.

F^‘_3-2=163 Н

6. Расчет колонны.

Определим суммарные реакции от действия всех сил (опоры А и В).

Σm_А=0:

R_B-2500 - G1200+Fcos14⁰225-Fsin14⁰Q36=0

R_B=120кН;

ΣF_у = 0;                                                          

R_Ау- G-Q -F sin 20⁰=0

R_Ах= R_В +F cos 20⁰

R_Ау= G+Q +F sin 30⁰

R_Ах=80,75 кН

R_Ау=78,7 кН

Определяем реакции в узлах 1 и 3:

Σm₁=0:

R₃2000- G1200-Q2500-F sin 30⁰2500+ F cos 30⁰2000=0

R₃=165000 Н

ΣF_х = 0;

R_1х- R₃ -F cos 20⁰=0

R_1х= R₃ +F cos 20⁰

R_1х=135 кН

R_Ау=78,7 Н

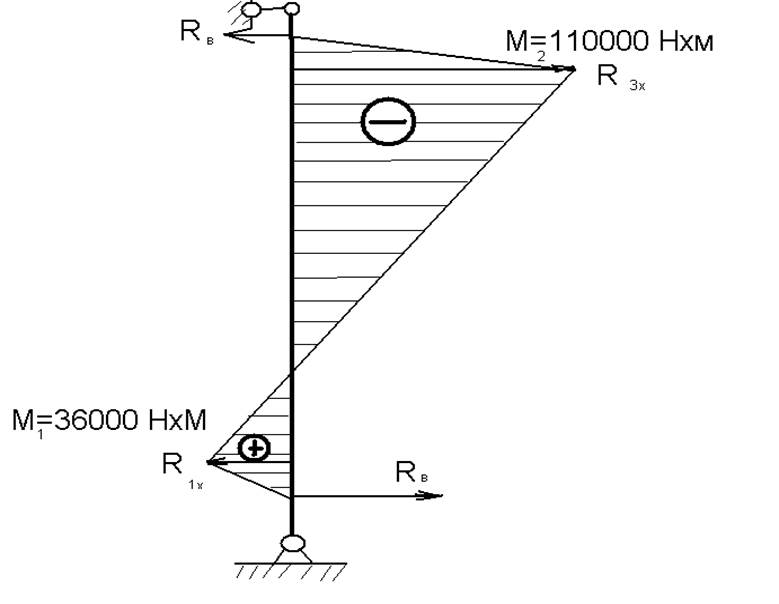
Рисунок 6.1- Эпюра изгибающих моментов в стержне 1

М₁= R_B 0,25

М₁= 1200,25=30   

М₂= R_B 2,25- R_1х 2,0

М₂= 120000 2,25- 135000 2,0=-110000 Н

Суммарные напряжения:

σ =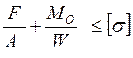                                                     (21)

σ 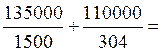 =160<168 МПа 

Условие выполняется.

          7.Расчет и конструирование узлов