Теоретические основы методов оценки показателей надежности. Метод расчета показателей надежности при использовании марковских процессов

3.  ТЕОРЕТИЧЕСКИЕ ОСНОВЫ МЕТОДОВ ОЦЕНКИ

ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ

3.1.  Метод расчета показателей надежности при использовании марковских процессов

В основе этого метода расчета надежности лежит описание функционирования энергоблоков марковским процессом с дискретным множеством состояний.

Метод используется в предположении экспоненциальных законов определения времени работы и восстановления l_i = const, m_i = const. Рассмотрим методические подходы к оценке надежности энергоблока на примере графа состояний (рис. 3.1) с двумя состояниями: работоспособным – 1, полного отказа – 2.

Стрелки графа указывают направления возможных изменений состояний. Переход из состояния 1 в состояние 2 осуществляется по принципу однородного марковского процесса с интенсивностью l(характеристикой является постоянство интенсивностей переходов). Переход из состояния 2 в 1 осуществляется с интенсивностью m,  так как энергоблок является восстанавливаемым.

Вероятность того, что в момент времени t + Dt энергоблок находится в состоянии 1 оценивается следующим алгоритмом. Очевидно, что в состоянии 1 энергоблок по истечении времени t + Dt может находится по двум причинам: 1.1 – в момент времени t он находился в состоянии 1 и за период Dt не перешел в состояние 2; 1.2 – в момент времени t энергоблок находился в состоянии 2 и за период времени Dt перешел в состояние 1.

Вероятность нахождения энергоблока в состоянии 1 по п. 1.1 определяется произведением Р₁(t) на вероятность (1-lDt) того, что энергоблок не перешел в состояние 2 за время Dt. Аналогично по п. 1.2 имеем Р₂(t)m×Dt. Используя правило сложения вероятностей, найдем

Р₁(t + Dt) = Р₁(t)(1-lDt) + Р₂(t)m×Dt

Преобразим это уравнение к виду:

.

При Dt ® 0 получим:

.

Подобные дифференциальные уравнения называются уравнениями Колмогорова. Очевидно, что подобное уравнение можно составить для каждого состояния графа. При этом граф состояний будет описываться системой дифференциальных уравнений, в которой их количество равно числу состояний на графе.

Для второго состояния энергоблока найдем

.

При составлении дифференциальных уравнений для каждого из состояний пользуются следующим математическим правилом. Производная вероятности (нахождения элемента в каждом из состояний) по времени равна алгебраической сумме произведений вероятностей состояний (связанных между собой стрелками на графе) на интенсивность переходов, при этом слагаемые берутся со знаком минус, если стрелка выходит из вершины, для которой записывается уравнение, и со знаком плюс, если стрелка входит в вершину графа.

Для решения системы уравнений Колмогорова дополнительно вводится уравнение нормировки

.

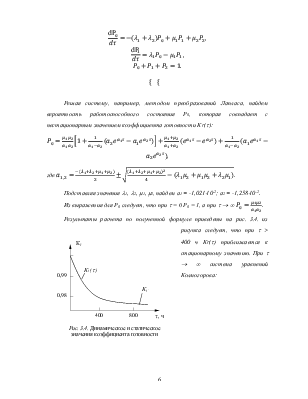
Применительно к графу на рис. 3.1 можно записать (опуская для простоты записи t):

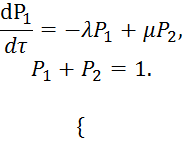
При Dt ® ¥ устанавливается стационарный режим, для которого система