Динамическое действие нагрузок. Понятие о динамическом нагружении. Статические и динамические нагрузки. Динамический коэффициент

массу действует сила инерции , равная произведению массы на ускорение 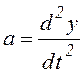 и направленная в сторону, ему противоположную:

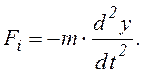
Прогиб балки y от этой силы:

                                                  (6.23)

где  – прогиб от единичной силы, приложенной в точке прикрепления массы.

Подставляя выражение  в уравнение (6.23), получим:

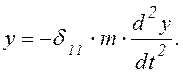                                       (6.24)

Разделим уравнение (6.24) на  и приведем его к виду

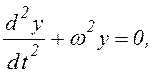                                            (6.25)

где

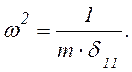                                               (6.26)

Выражение (6.25) представляет собой дифференциальное уравнение собственных колебаний системы с одной степенью свободы.

Решение этого уравнения

                                       (6.27)

определяет положение колеблющейся массы в момент времени t.

Обозначив постоянные интегрирования как ; , представим выражение (6.27) в виде

                                       (6.28)

где А – амплитуда колебаний,  – фаза колебаний, – сдвиг фазы.

Колебания, описываемые уравнением (6.28), носят название простых гармонических колебаний.

Скорость движущейся массы можно найти так:

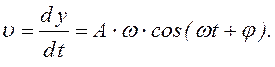                                 (6.29)

Произвольные постоянные А и  определяются с учетом начальных условий:

при

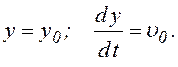
Тогда из уравнений (6.28) и (6.29) имеем:

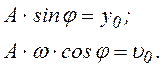
Возведем в квадрат правые и левые части полученных выражений и почленно сложим, в итоге получим:

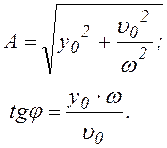                                         (6.30)

График изменения перемещения у во времени показан на рис. 6.14.

Наибольшее отклонение возникает тогда, когда выражение принимает значение, равное единице. Из уравнения (6.28) следует, что отклонение будет равно постоянной величине А, называемой амплитудой колебаний.

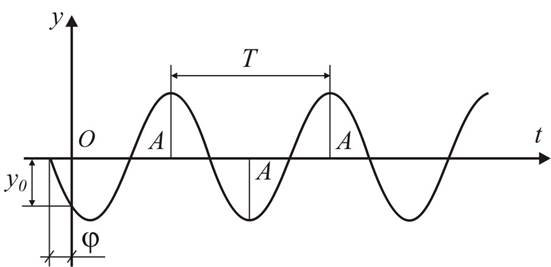
Рис. 6.14

Время Т, за которое совершается один цикл колебаний, называется периодом колебаний. Через каждые T секунд отклонение у приобретает прежнее значение

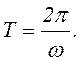                                              (6.31)

Откуда число колебаний в 2π секунд равно

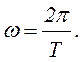
В соответствии с выражением (6.26) имеем

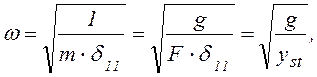                          (6.32)

где – круговая частота собственных колебаний с^-1 (число колебаний в 2π  секунд).

Собственные колебания быстро затухают (рис. 6.15) из-за наличия сил сопротивления (сопротивление воздуха, трение в подшипниках, силы внутреннего неупругого сопротивления и т.д.).

Если масса m закреплена в середине пролета двухопорной балки (рис. 6.12), то прогиб  от единичной силы определяется равенством

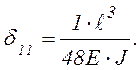   Тогда 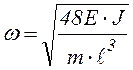.                             (6.33)

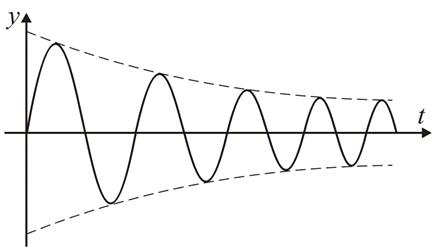
Рис. 6.15

Из формулы (6.33) следует, что частота колебаний повышается с ростом жесткости балки и уменьшается с увеличением пролета и массы m.

6.4.3. Вынужденные колебания упругой системы

Если на систему действует возмущающая сила , изменяющаяся во времени по какому-либо закону, то колебания балки, вызванные этой силой, называют вынужденными. После приложения силы инерции 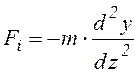 балку в отклоненном состоянии можно рассматривать как находящуюся в равновесии (рис. 6.16).

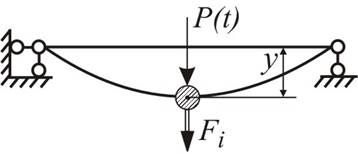
Рис. 6.16

Перемещение у теперь уже нужно определять от двух сил –  и :

где δ₁₁ – прогиб от единичной силы, приложенной в месте прикрепления массы.

Заменим силу инерции ее значением и перенесем неизвестные в левую часть. После деления всех членов уравнения на  получим дифференциальное уравнение вынужденных колебаний:

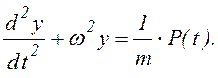                                 (6.34)

Решение этого уравнения состоит из двух частей: решения однородного уравнения и частного решения, зависящего от вида правой части.

Рассмотрим частный случай, когда внешняя сила представляет собой вибрационную (периодическую) нагрузку, меняющуюся по гармоническому закону с частотой :

С учетом последнего равенства уравнение (6.34) примет вид

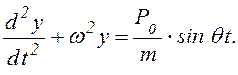                                       (6.35)

Его решение представляет собой выражение (6.28), полученное в п.6.4.2. Частное решение имеет следующий вид:

, где  - амплитуда вынужденных колебаний;  - частота этих колебаний.

Подставив частное решение в уравнение (6.35), найдем, что

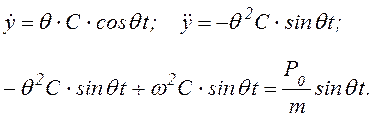
Отсюда после сокращения на sin  получим:

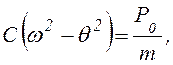    или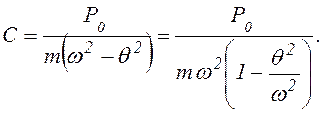    

Если учесть, что из формулы (6.32)

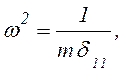
то получим

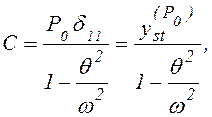                                            (6.36)

где 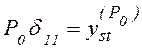 - прогиб от статически приложенной силы .

Таким образом, решение уравнения (6.35) имеет вид

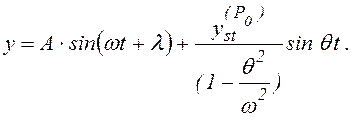                              (6.37)

Первое слагаемое этого выражения представляет собой собственные колебания, а второе – вынужденные.

Так как собственные колебания в реальных балках быстро затухают, то рассмотрим только вынужденные, которые происходят с частотой .

Амплитуда вынужденных колебаний С (т.е. наибольшее отклонение  стержня от первоначального  положения) будет найдена, если принять :

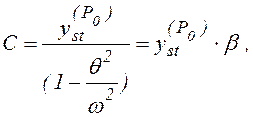
где  – коэффициент нарастания колебаний:

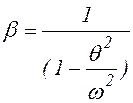.                                              (6.38)

Тогда амплитуда вынужденных колебаний равна

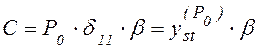.                                   (6.39)

6.4.4. График изменения коэффициента нарастания колебаний

Явление резонанса

График для абсолютного значения величины коэффициента нарастания