






























В главах первой части были рассмотрены простейшие виды нагружения бруса: осевое растяжение и сжатие, сдвиг, кручение и прямой изгиб. В реальных условиях элементы конструкций часто подвергаются воздействию различных комбинаций простых нагружений. Такие случаи называют сложным сопротивлением.
Под сложным сопротивлением бруса деформированию понимают такие сочетания простых нагружений, когда в его сечениях одновременно возникают несколько внутренних силовых факторов.
В основе расчетов на сложное сопротивление лежит принцип независимости действия сил, согласно которому напряжения и деформации, вызванные комбинацией силовых факторов, определяются как сумма (алгебраическая или геометрическая) напряжений и деформаций от каждого фактора в отдельности. Данный принцип применим во всех случаях, когда рассматриваются малые деформации в пределах справедливости закона Гука.
Рассмотрим основные виды сложного сопротивления: косой изгиб, внецентренное сжатие (растяжение), изгиб с кручением.
1.2.1. Плоский и пространственный косой изгиб
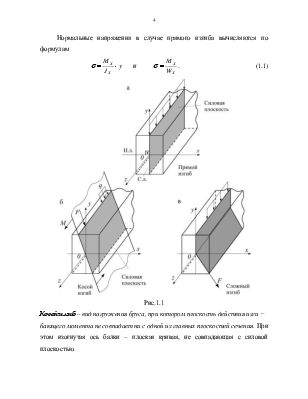
В случае прямого изгиба силовая плоскость совпадает с одной из главных плоскостей инерции, например – yOz (рис 1.1 а). При этом силовая линия (с.л.) и нейтральная линия (н.л.) взаимно перпендикулярны, а изогнутая ось балки лежит в силовой плоскости.
![]()
![]() Нормальные напряжения в
случае прямого изгиба вычисляются по формулам
Нормальные напряжения в
случае прямого изгиба вычисляются по формулам
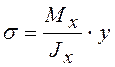 и
и 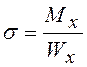 . (1.1)
. (1.1)
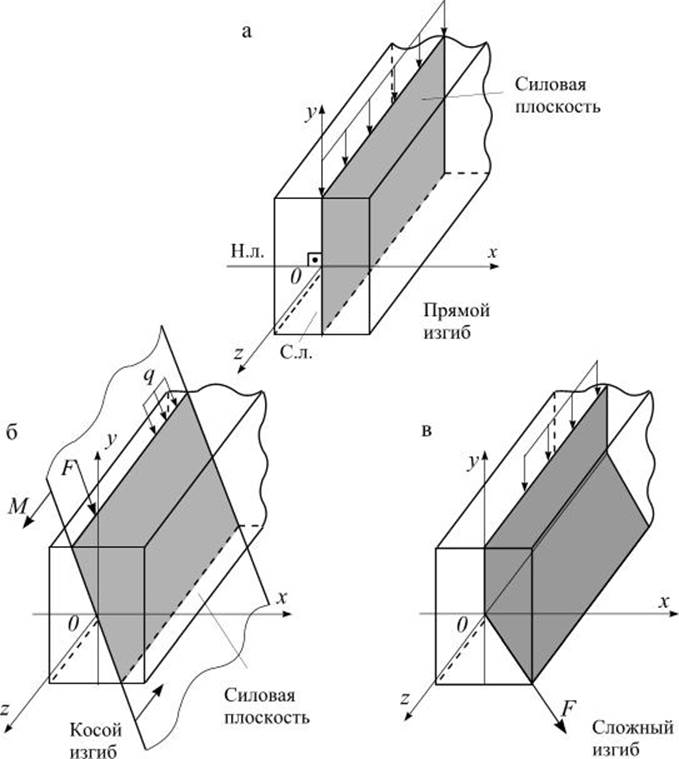
Рис.1.1
Косой изгиб – вид нагружения бруса, при котором плоскость действия изги −
бающего момента не совпадает ни с одной из главных плоскостей сечения. При этом изогнутая ось балки – плоская кривая, не совпадающая с силовой плоскостью.
Если косой изгиб вызван нагрузками, действующими в одной плоскости (силовой), то изгиб называют плоским (рис.1.1б). Если нагрузки действуют в разных продольных плоскостях, то это сложный, или пространственный, изгиб (рис. 1.1 в). Изогнутая ось балки – не плоская кривая.
Плоский и сложный косой изгиб
рассматривают как совокупность двух прямых изгибов, для чего нагрузки, лежащие в
продольных плоскостях, раскладывают на составляющие, расположенные в главных
плоскостях xОz и yОz. В
поперечных сечениях бруса в общем случае возникают 4 внутренних силовых
фактора: ![]() . Проводя расчет на прочность при
косом изгибе, обычно пренебрегают влиянием касательных напряжений.
. Проводя расчет на прочность при
косом изгибе, обычно пренебрегают влиянием касательных напряжений.
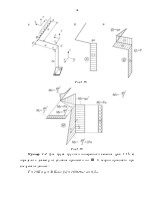
Примеры из инженерной практики
Брус обрешетки
кровли (рис. 1.2 а) нагружен по схеме косого изгиба. Вертикальная нагрузка F от веса кровли и собственного веса
обрешетки наклонена к главной оси у под некоторым углом ![]() .
.
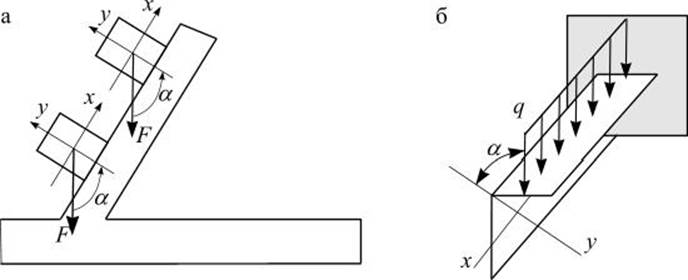
Рис.1.2
Уголок, заделанный одним концом в стену (рис. 1.2 б), также нагружен по схеме косого изгиба, так как главные оси сечения – x и y – наклонены под не которым углом α к погонной нагрузке q (это вес 1-го метра уголка).
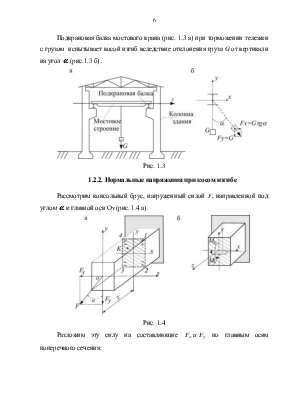
Подкрановая балка
мостового крана (рис. 1.3 а) при торможении тележки с грузом испытывает косой
изгиб вследствие отклонения груза G от вертикали на угол ![]() (рис.1.3 б)
.
(рис.1.3 б)
.
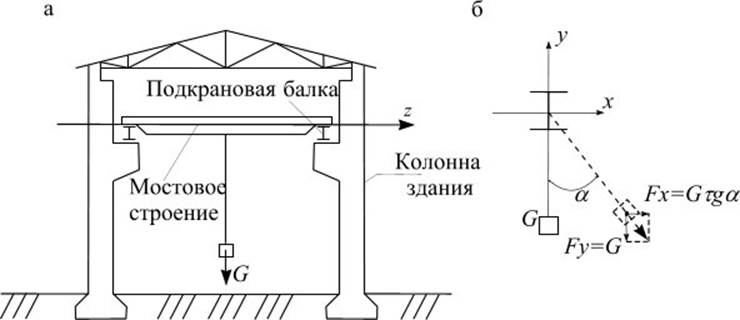
Рис. 1.3
1.2.2. Нормальные напряжения при косом изгибе
Рассмотрим
консольный брус, нагруженный силой F, направленной под углом ![]() к главной оси Оу
(рис. 1.4 а).
к главной оси Оу
(рис. 1.4 а).
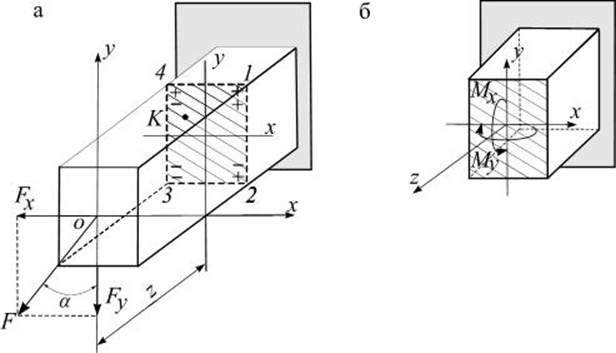
Рис. 1.4
![]() Разложим эту силу на составляющие
Разложим эту силу на составляющие ![]() по
главным осям поперечного сечения:
по
главным осям поперечного сечения:
![]()
Каждая из этих
составляющих вызывает прямой изгиб бруса: ![]() – в
плоскости zОy,
– в
плоскости zОy, ![]() – в плоскости zОx. Изгибающие моменты в произвольном
сечении бруса (рис.1.4 б) находятся так:
– в плоскости zОx. Изгибающие моменты в произвольном
сечении бруса (рис.1.4 б) находятся так:
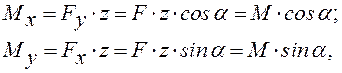
![]()
где 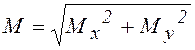 -
полный изгибающий момент в плоскости действия силы F.
-
полный изгибающий момент в плоскости действия силы F.
Нормальные напряжения в сечении согласно принципу независимости действия сил определяются как сумма
![]() .
.
С учетом (1.1)
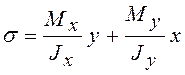 .
(1.2)
.
(1.2)
По формуле (1.2)
определяются нормальные напряжения в любой точке сечения при косом
изгибе. Причем моменты ![]() и
и ![]() , а также координаты х и у исследуемой
точки подставляют по абсолютному значению, а знаки слагаемых напряжений
устанавливают исходя из характера деформирования бруса.
, а также координаты х и у исследуемой
точки подставляют по абсолютному значению, а знаки слагаемых напряжений
устанавливают исходя из характера деформирования бруса.
Так, ![]() вызывает изгиб, при котором верхние
волокна растянуты, нижние - сжаты
вызывает изгиб, при котором верхние
волокна растянуты, нижние - сжаты
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.