Теоретические основы налогового менеджмента. Функции и задачи налогового менеджмента. Матрично-балансовый метод в налоговом менеджменте

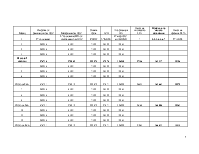
оборот по дебету счета (сумма всех элементов соответствующей строки);

S_К - оборот по кредиту счета (сумма всех элементов соответствующего столбца);

SS - сумма всех хозяйственных операций и действий.

Частным случаем матрицы является вектор. Вектор это матрица, состоящая из одного столбца (вектор-столбец) или одной строки (вектор-строка). В проводимых рассуждениях предпочтение отдается вектору-столбцу, который в дальнейшем будет именоваться просто вектором.

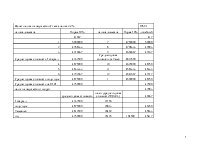
Для того чтобы составить традиционный бухгалтерский регистр под названием «оборотно-сальдовая ведомость», необходимо выделить из матрицы журнала хозяйственных операций соответствующие обороты (хозяйственные суммарные действия за отчетный период по определенным финансово экономическим направлениям и параметрам) - по дебету и кредиту.

Согласно теории матриц, это можно осуществить, путем умножения матрицы (справа) на следующий окаймленный вектор (вектор-столбец) перехода В [6]:

Для удобства справа от вeктopа-перехода приведены номера соответствующих счетов.

Обороты по дебету и кредиту счетов в матрично-векторной форме могут быть получены  согласно следующим формулам [6]:

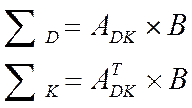,                                           (1.3)

где: - транспонированная матрица по отношению к матрице А_DK. Транспонированной называется матрица, у которой изменены места столбцов и строк по сравнению с исходной матрицей.

Обратимся к общему уравнению баланса, которое отражает равенство сумм актива и пассива, т.е. соответствие сумм имеющихся в наличии материальных и нематериальных ценностей предприятия величине источников их возникновения и существования [6]:

А=Р,                                                       (1.4)

где А - постатейные активы (актив баланса);

Р - постатейные пассивы (пассив баланса).

Это уравнение может быть преобразовано в окаймленный вектор, который отображает сальдо (начальное и/или конечное) оборотно-сальдовой ведомости [6]:

где S - сальдо (остатки) по счетам бухгалтерского баланса на начало или на конец периода, соответствующие упомянутым экономическим категориям (материальным и нематериальным ценностям, а также источникам их возникновения).

Сумма вектора, отображающего сальдо по бухгалтерским счетам, равна нулю, что естественным образом вытекает из уравнения (1.4).

Если присвоить начальному сальдо индекс 1, а конечному – индекс 2, то уравнение оборотно-сальдовоro баланса (или оборотно-сальдовой ведомости) будет выглядеть следующим традиционным образом [6]:

S₂ = S₁ + S_D - S_K.                                                  (1.6)

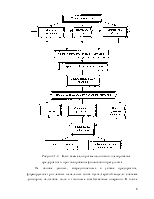
Таким образом, последовательность действий бухгалтера, который использует матричную алгебру, при расчетах оборотно-сальдовой ведомости такова:

- путем умножения матрицы (и транспонированной матрицы) шахматной ведомости на вектор перехода по формулам (1.3) определяются векторы дебетовых и кредитовых оборотов по всем используемым счетам;

- по формуле (1.5) рассчитывается вектор начального сальдо;

- по уравнению (1.6), исходя из вектора начального сальдо и векторов дебетовых и кредитовых оборотов, вычисляется вектор конечного сальдо.

Для того, чтобы получить зависимость величины чистой прибыли от какого либо параметра (элемента) матрицы хозяйственных операций, необходимо провести следующие действия.

Поскольку каждый элемент матрицы зависит от некоторых других, изменяя его, следует корректировать элементы, с ним связанные. Эти связи, как правило, легко устанавливаются в каждом конкретном случае. Они обусловлены экономическими требованиями, налоговым законодательством и вероятностными факторами.

Тогда для каждого численного значения выбранного параметра получается своя матрица хозяйственных операций. Далее для каждого значения параметра производятся расчеты по формулам (1.3 и 1.9) [6].

S₀ = S_D - S_K,                                                          (1.9)

где S₀ – сальдо (остатки) по счетам хозяйственной деятельности предприятия, моделируемой в виде замкнутой денежной системы. Этот вектор можно назвать вектором результатов.

В результате этих расчетов получится требуемое количество векторов по действующему плану счетов (формула 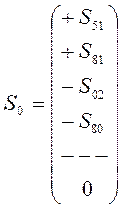1.10)

,                                         (1.10)

или по Новому (формула 1.11) [6].

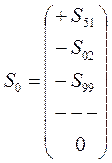,                                         (1.11)

Их них выбирается соответствующее значение чистой прибыли.

Алгоритм для решения задачи налогового планирования и прогнозирования финансового результата имеет важную отличительную особенность, состоящую в том, что основным критерием сравнимости различных вариантов является величина чистой прибыли.

При прочих равных условиях данный критерий считается наиболее