Расчёт вероятности безотказной работы зубчатых передач по критерию сопротивления контактной усталости

Санкт - Петербургский Государственный Университет Низкотемпературных и Пищевых Технологий

Кафедра «Деталей машин и основ инженерного проектирования»

Доклад

«Расчёт вероятности безотказной работы зубчатых передач по критерию сопротивления контактной усталости»

Выполнили:                                                                   

студенты  гр.                                                     

Руководитель:                                                          

Санкт-Петербург

2005 г.

Введение

Надежность – это свойство объекта сохранять во времени в установленных пределах все параметры, обеспечивающие выполнение требуемых функций в заданных условиях эксплуатации.

Первостепенное значение надежности в технике связанно с тем, что уровень надежности в значительной степени определяет развитие техники по основным направлениям: автоматизации производства, интенсификации рабочих процессов и транспорта, экономии материалов и энергии. Современные технические средства состоят из множества взаимодействующих механизмов, аппаратов и приборов. Отказ в работе хотя бы одного ответственного элемента сложной системы может привести к нарушению работы всей системы.

Недостаточная надежность оборудования приводит к огромным затратам на ремонт, простою оборудования, не выполнению ответственных задач, иногда к авариям, связанным с большими экономическими потерями, разрушением крупных объектов и к человеческим жертвам.

Показатели надежности различаются в соответствии с компонентами надежности на показатели безотказности, долговечности ремонтопригодности и сохраняемости. Используемые критерии характеризуют общий уровень надежности, и абсолютные или числовые показатели, характеризующие отдельные типоразмеры машин.

Надежность изделий в зависимости от их вида может оцениваться частью или всеми показателями надежности, на которые влияет ряд факторов.

В расчетах надежности многие параметры должны рассматриваться как случайные величины, т.е. такие которые могут принять то или иное значение, неизвестное заранее. К случайным факторам относятся, например: неоднородность физико-механических свойств обрабатываемого материала и инструмента, отклонения при выполнении предшествующих операций в технологическом процессе и т.д.

Исследования случайных процессов ведется вероятностными методами.

Эти процессы позволяют установить связь между рассматриваемыми случайными величинами и вероятностью их проявления в процессе производства, и тем самым повысить надежность.

Любая связь между случайной величиной и вероятностью ее появления при многократных испытаниях называется законом распределения. Методами теории вероятности можно пользоваться лишь при многократном воспроизведении одинаковых условий. Соответствующие испытания должны повторяться возможно большее число раз (не менее 50…100).

Случайные величины (СВ) могут быть прерывными (дискретными) и непрерывными. Возможные значения прерывных CВ могут быть заранее перечислены. Значения непрерывных CВ заранее неизвестны.

Закон распределения для непрерывных случайных величин может быть получен в 2х формах: интегральной и дифференциальной.

Интегральная форма закона распределения, заключается в том, что случайная величина x меньше некоторого текущего значения Х.

В теории вероятности доказано, что, если в каком-то явлении действует большое число независимых случайных причин, причем действие каждой из них, мало по сравнению с суммарным, то суммарная непрерывная, случайная величина будет распределена по нормальному закону. Рассмотрим расчет вероятности безотказной работы зубчатых передач, входящих в состав двухступенчатого редуктора.

Расчет на сопротивление контактной усталости

Вероятность безотказной работы по критерию сопротивления контактной усталости определяется как вероятность того, что контактное напряжение не превышает предела контактной выносливости .

Контактное напряжение , МПа, действующее в полюсе зацепления,

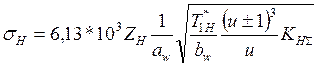, где

 - коэффициент, учитывающий форму сопряженных поверхностей;  - межосевое расстояние, мм;  - рабочая ширина венца, мм;  - передаточное число;  - крутящий момент на шестерне при работе в номинальном режиме (сокращенно номинальный момент), Н*м;  - коэффициент нагрузки.

Напряжение  рассматриваем как функцию случайной величины , равной произведению четырех случайных величин:

где  - коэффициент внешней нагрузки;  - учитывающий распределение нагрузки по ширине венца;  - коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении;  - коэффициент, учитывающий распределение нагрузки между зубьями.

Частные коэффициенты- являются зависимыми случайными величинами