где Pi, Pj – активные нагрузки в узлах; Qi, Qj – реактивные нагрузки; rij ri, rj – собственные и взаимные активные
сопротивления узлов; ![]() - разности
фаз узловых напряжений; m – число узлов сети.
- разности
фаз узловых напряжений; m – число узлов сети.
Для схемы электроснабжения, представленной на рисунке 1 формула выглядит следующим образом:
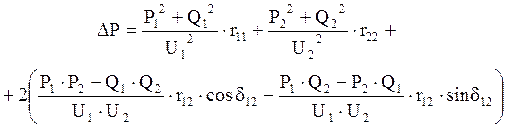 (4.8)
(4.8)
где r11, r12, r22 – собственные и взаимные активные сопротивления узлов, определяемые по формулам:
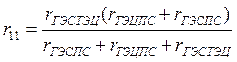 (4.9)
(4.9)
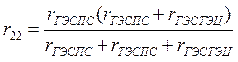 (4.10)
(4.10)
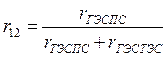 (4.11)
(4.11)
Введем переменные потерь в сетях:
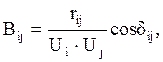 (4.12)
(4.12)
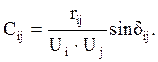 (4.13)
(4.13)
Считаем, что
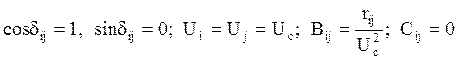
Тогда потери электроэнергии будут равны:
![]() (4.14)
(4.14)
Так как нам не известны значения реактивных мощностей, то мы их не учитываем, тогда выражение (4.14) запишется следующим образом:
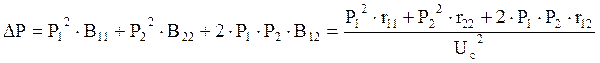 (4.15)
(4.15)
Продифференцируем выражение (4.14):
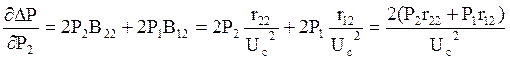 ; (4.16)
; (4.16)
Запишем выражение (4.6) для ТЭЦ узла 1 (рисунок 1) с учетом выражения (4.16):
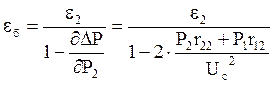 , (4.17)
, (4.17)
Из уравнения (4.17) выразим удельные приросты ТЭС:
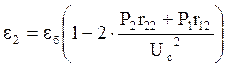 .
(4.18).
.
(4.18).
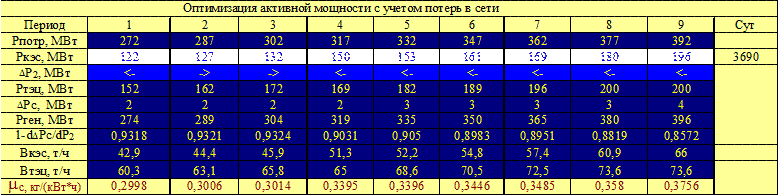
Порядок расчета оптимального распределения активной мощности с учетом потерь в электроэнергетической системе:
1. Задаем величину удельного прироста электростанции в балансирующем узле (ГЭС).
2. Определяем величину удельного прироста ТЭЦ по формуле (4.18).
3. По характеристики удельных приростов находим вырабатываемую ТЭЦ электроэнергию.
4. Проверяем баланс активной мощности (4.2). Должна соблюдаться сходимость до 1 МВт. Если условие не выполняется, то необходимо изменить активную мощность, вырабатываемую на ГЭС и повторить этапы расчета.
Оптимизация распределения реактивных нагрузок и уровней напряжений в ЭЭС
Оптимальное распределение нагрузки между регулируемыми источниками реактивной мощности производится по упрощенному методу, где допускают, что модули напряжения в узлах и фазы узловых напряжений не зависят от реактивной нагрузки узла, т. е. являются постоянными. Тогда полная величина потерь активной мощности в сети будет находиться:
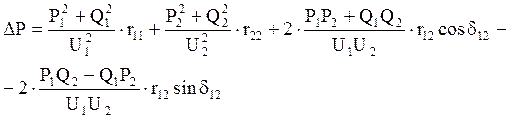 (5.1)
(5.1)
Взяв производную от (5.1) по Q1, Q2 и решив полученную систему уравнений, можно найти оптимальные значения Q1 и Q2:
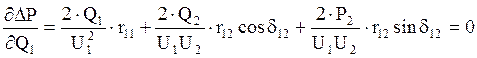 ,
,
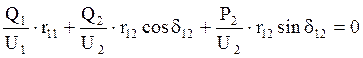 ,
,
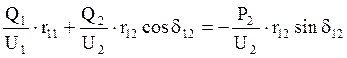 , (5.2)
, (5.2)
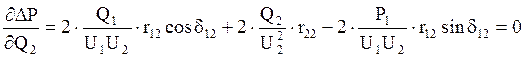 ,
,
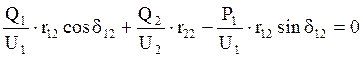 ,
,
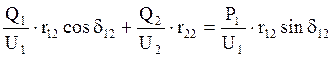 . (5.3)
. (5.3)
Составим систему уравнений из (5.2), (5.3), введя дополнительные переменные, и решаем её матричным способом:
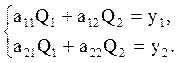 (5.4)
(5.4)
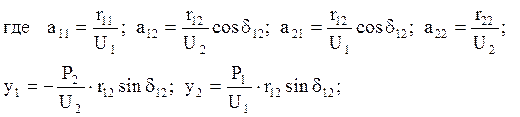
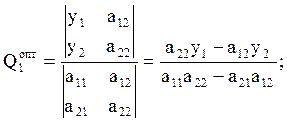 (5.5)
(5.5)
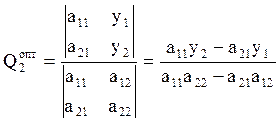 ; (5.6)
; (5.6)
В узле 1 (потребитель) генерируемая реактивная мощность складывается из следующих составляющих:
![]() , (5.7)
, (5.7)
где Qн – потребляемая реактивная мощность реактивная мощность; QСК – реактивная мощность синхронного компенсатора; Qзар.1 - зарядная реактивная мощность. Q1 будет оптимальной в том случае, если QСК оптимальна, т. е.:
![]() , (5.8)
, (5.8)
Во втором узле:
![]() , (5.9)
, (5.9)
где QГ – реактивная мощность генератора. Q2 будет оптимальной в том случае, если QГ оптимальна, т. е.:
![]() , (5.10)
, (5.10)
Если QСК < ![]() тогда
выводим QСК числа
переменных и решаем оптимизационную задачу по одному параметру QГ, т. е. фиксируем мощность исходного
синхронного компенсатора на максимуме и получаем режим, когда
тогда
выводим QСК числа
переменных и решаем оптимизационную задачу по одному параметру QГ, т. е. фиксируем мощность исходного
синхронного компенсатора на максимуме и получаем режим, когда ![]() , а
, а ![]() .
.
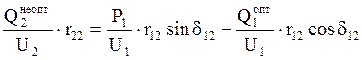 ,
,
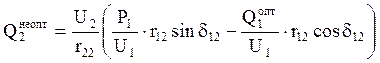 . (5.11)
. (5.11)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.