Определение характеристики относительных приростов затрат и расходной характеристики теплоэлектроцентрали (ТЭЦ), страница 3

Параметры суточного графика нагрузки приведены в таблице 2.1.

Предварительно примем  0,05. Потребление энергосистемы  269 МВт. Зададим нагрузку ГЭС  90 МВт. В соответствие таблице 1.6 относительный прирост затрат ГЭС равен  6,04 м³/(с·МВт). Относительный прирост затрат ТЭЦ равен  0,05·6,04 = 0,302 кг/(кВт·ч). В соответствие таблице 1.5 нагрузка ТЭЦ равна  163 МВт. Баланс мощности ЭЭС равен  163 + 90 – 269 = -16 МВт. Баланс мощности меньше нуля, поэтому увеличим нагрузку балансирующей электростанции на величину небаланса 16 МВт. Принимаем  116 МВт. Относительный прирост затрат ГЭС равен  6,4 м³/(с·МВт). Относительный прирост затрат ТЭЦ равен  0,05·6,4 = 0,32 кг/(кВт·ч). Баланс мощности при этом равен  163 + 116 – 269 = 0. Результаты аналогичных расчетов сведены в таблице 2.2. Соответствующий средний суточный расход воды равен  557 м³/с. Полученное значение расхода воды необходимо увеличить, для этого уменьшим значение неопределенного множителя .

Примем следующее значение  0,045. Для нового значения проведем аналогичные расчеты. Результаты расчетов сведены в таблице 2.2. Средний суточный расход воды ГЭС равен  642 м³/с. Полученное значение расхода превышает заданное значение.

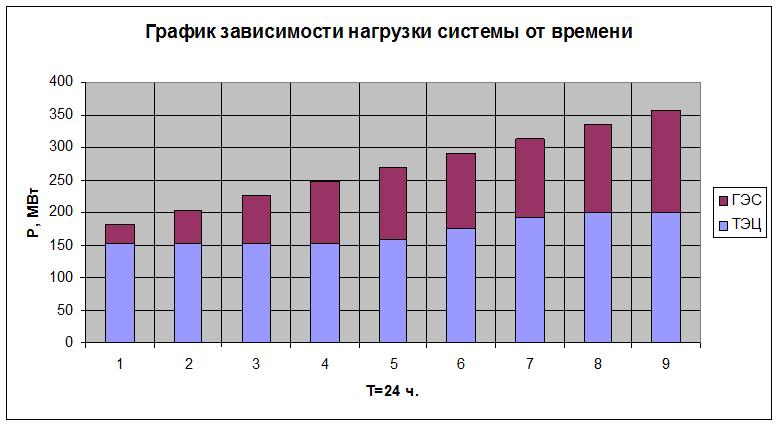
Методом линейной интерполяции для заданного среднего суточного расхода  610 м³/с определим значение неопределенного множителя Лагранжа  0,047802. После аналогичных расчетов определен средний суточный расход воды равный  610 м³/с. Результаты расчетов сведены в таблицу 2.1 и представлены на рисунке 2.1.

Таблица 2.1:

«Оптимизация активных нагрузок в энергосистеме с гидроэлектростанцией».

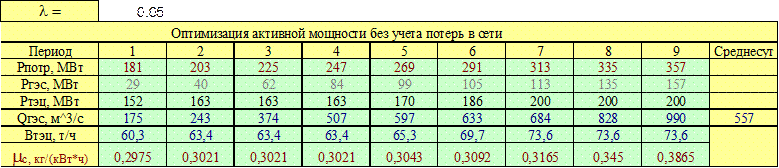
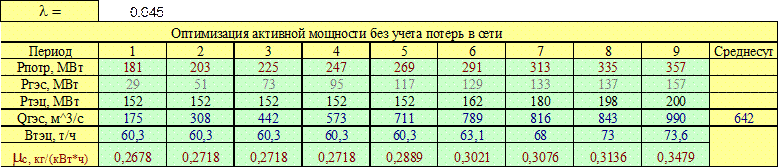
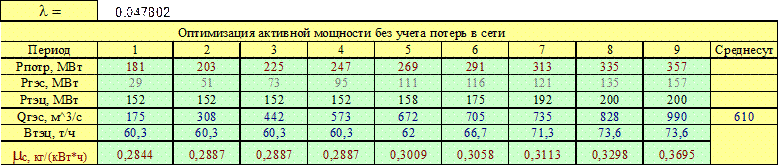
Рис 2.1:

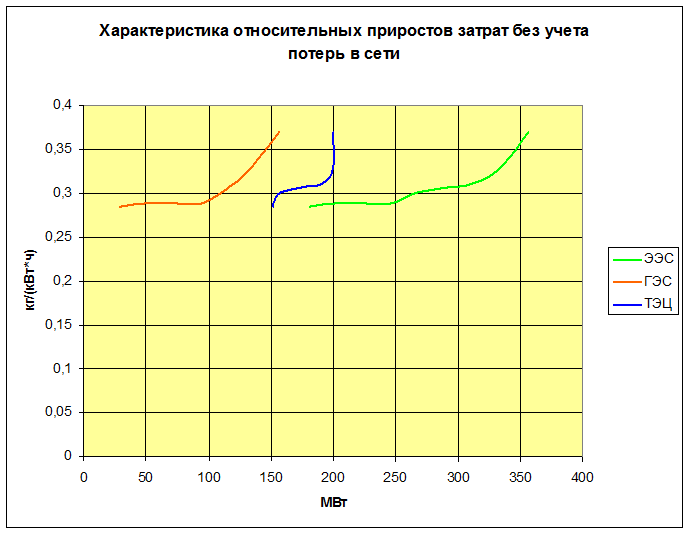
Рис. 2.2:

Определение потерь в электрической сети

Исходные данные:

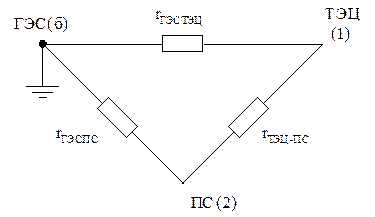
Рисунок 1 – схема электроэнергетической системы.

Оптимальное распределение генерации активной мощности в электроэнергетической  системе с ТЭС достигается в случае, когда:

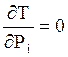,                                                (4.1)

где Т – затраты на выработку электрической энергии; Р_i – генерируемая  электростанцией активная мощность.

Решение данной системы уравнений достигается методом неопределенного множителя Лагранжа.

Для этого вводят дополнительную функцию баланса активной мощности с учетом потерь:

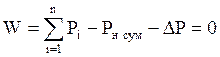,                                 (4.2)

где – сумма генерируемых мощностей всех узлов, - суммарная нагрузка,  - потери в сети.

Функция Лагранжа:

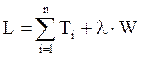,                                         (4.3)

где - неопределенный множитель.

Взяв производную, получаем следующее выражение:

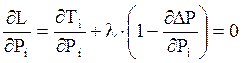,                               (4.4)

где 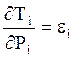 – удельные приросты затрат производства электроэнергии.

Находим неопределенный множитель:

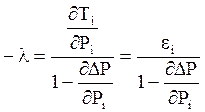                                   (4.5)

Где 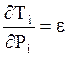 - удельный прирост ТЭС.

Следовательно, условие оптимального распределения электроэнергетической системы будет:

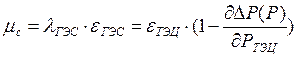,                         (4.6)

Потери в общем виде определяются по формуле:

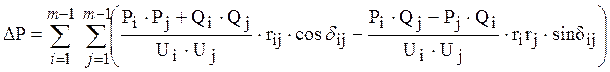, (4.7)