Оптимизация режима работы энергосистемы. Оптимальная активная нагрузка электростанции. Определение характеристики относительных приростов затрат и расходной характеристики теплоэлектроцентрали, страница 5

При одной и той же нагрузке оптимальному числу агрегатов соответствует меньший расход воды. Переход на меньшее число агрегатов экономично в тех же границах. Оптимальные зоны работы при различном числе включенных агрегатов в таблицах 1.8÷1.10 выделены жирным. Соответствующие характеристики относительных приростов затрат при оптимальном числе агрегатов имеют кусочно-возрастающею зависимость (рис. 1.13). Для исключения разрывного характера функции производится ее спрямление. Спрямление производится по правилу равенства площадей ХОП выше и ниже линии расчетного значения относительных приростов затрат при соответствующих переходах. Физическим смыслом площади фигуры в осях относительные приросты затрат – нагрузка является расход воды. Таким образом, обеспечивается равенство расхода воды ГЭС по фактической и спрямленной характеристикам.

  4. Оптимизация  распределения  активных  нагрузок  в  энергосистеме  из  тепловой  и  гидроэлектростанции  без  учета  потерь  в  сети 

Оптимизация активных нагрузок в энергосистеме из тепловой и гидроэлектростанции по критерию заданного среднего суточного расхода воды ГЭС  440 м³/(с·МВт). В балансирующем узле принимается ГЭС.

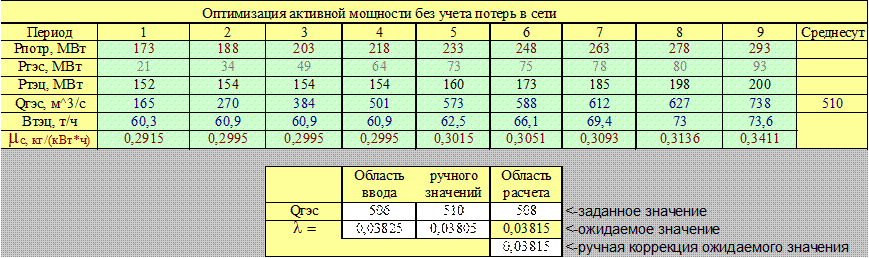
Методом линейной интерполяции для заданного среднего суточного расхода  508 м³/с определим значение неопределенного множителя Лагранжа  0,03815. После аналогичных расчетов определен средний суточный расход воды равный  510 м³/с. Разница между полученным и заданным расходом воды примерно 1 %. Полученное значение  можно считать результатом расчета.     Для любого из указанных интервалов времени i программно решается система уравнений

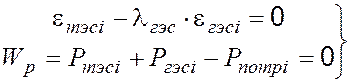,                                        (2)

где  неопределенный множитель Лагранжа (имеет постоянное значение в любом интервале времени суток),  соответственно нагрузки ТЭС, ГЭС и потребление ЭЭС для интервала времени i, МВт.

Когда баланс относительных приростов и активной мощности равны нулю, это оптимальное распределение активной мощности.

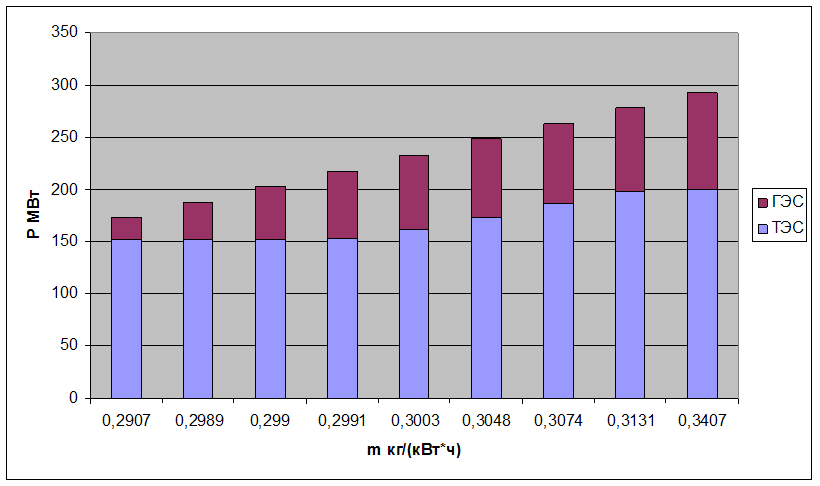
Из-за того что регулирующий диапазон на ГЭС больше чем на ТЭЦ, и водные ресурсы в стоимостном выражении меньше чем на ТЭЦ выгодно покрывать максимум потребления мощности с помощью ГЭС.
5. Определение потерь в сети.

Оптимальное распределение активной нагрузки электростанций с  учетом потерь в электрической сети.

Потери активной мощности в электрической сети определяются на основе расчетов установившихся режимов. Расчет установившихся режимов ЭЭС в настоящее время в основном производится методами Зейделя и Ньютона. Для определения удельных приростов потерь в сети имеет преимущество метод расчета с помощью матрицы собственных и взаимных сопротивлений узлов. Рассмотрим расчет удельных приростов потерь активной мощности с помощью матрицы сопротивлений. Потери активной мощности в электрической сети, МВт, представляются следующим образом

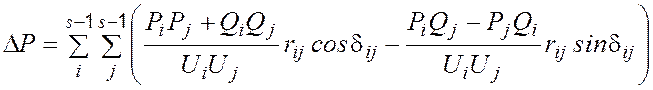,    (1.37)