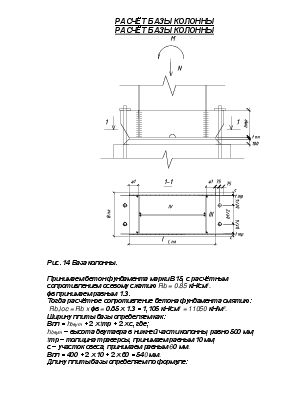
Расчёт колонны. Определение расчётных длин. Подбор сечения в верхней части колонны. Расчётная схема траверсы с эпюрами. Эпюра напряжений

РАСЧЁТ КОЛОННЫ

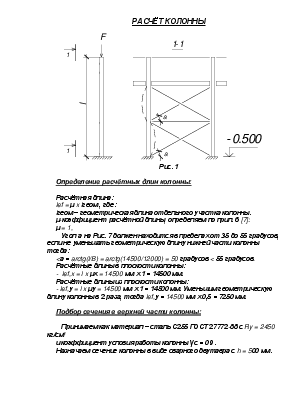
Рис. 1

Определение расчётных длин колонны:

Расчётная длина:

lef = μxlгеом., где:

lгеом – геометрическая длина отдельного участка колонны.

μ-коэффициент расчётной длины, определяем по прил. 6 [7]:

μ = 1,

   Угол а на Рис. 7 должен находится в пределах от 35 до 55 градусов, если не уменьшать геометрическую длину нижней части колонны тогда:

<а = arctg(l/B) = arctg(14500/12000) = 50 градусов < 55 градусов.

Расчётные длины в плоскости колонны:

-  lef,x = lxμх = 14500 мм х 1 = 14500 мм.

Расчётные длины из плоскости колонны:

- lef,у = lxμу = 14500 мм х 1 = 14500 мм. Уменьшим геометрическую длину колонны в 2 раза, тогда lef,у = 14500 мм х 0,5 = 7250 мм.  

Подбор сечения в верхней части колонны:

   Принимаем как материал – сталь С255 ГОСТ 27772-88 с Ry = 2450 кг/см²

и коэффициент условия работы колонны γс = 0.9.

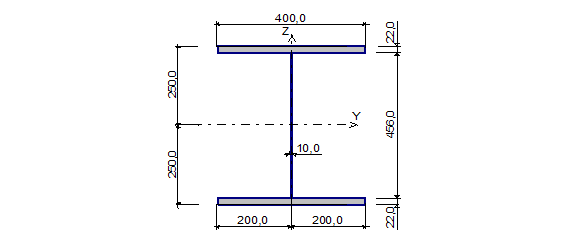
Назначаем сечение колонны в виде сварного двутавра с h = 500 мм.

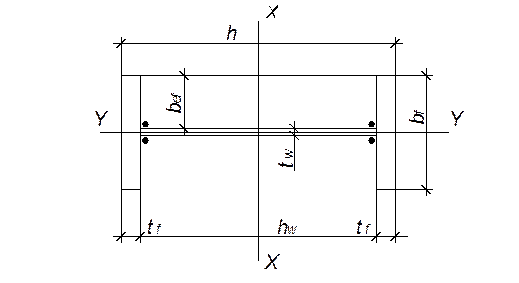
Рис. 2 Сечение верхней части колонны.

Из распечатки выписываем:    

Расчет верхней части колонны выполнять от сочетания :

N =-108,895 т=-1068,26 кН; M = 55,013 т*м=539,68 Кн*м.

Эксцентриситет: е = M/N = 539,68/1068,26 = 0.51 м = 51 см.

Определим требуемую площадь верхней части колонны:

Атр ≥ N/(ϕxRyxγс), где:

N – усилие в колонне;

Ry – расчётное сопротивление стали по пределу текучести;

ϕ – коэффициент снижений расчётных сопротивлений при внецентренном сжатии.

ϕ = f( mef, λусл), где:

mef – приведённый относительный эксцентриситет;

λусл – условная гибкость, которая определяется:

λусл = λ х (Ry/E) ^0.5 , где:

λ – гибкость;

λ = lef,x2/ iх, где:

iх – радиус инерции, принимаем равным 0.42 х h = 0.42 х 500 = 210 мм.

λ = 14500/210 = 69,048.

Е – модуль упругости 1 рода для стали равен 2.06 х 10 ⁵ МПа.

λусл = 69,048 х (245/(2.06 х10 ⁵)) ^0.5 = 2,43.

mef = mx х η, где:

mx – относительный эксцентриситет:

mx = е х 1/ρ, где:

ρ = 0.33 х h = 0.33 х 500 = 165 мм.

mx = 510/165 =3,09.

Отношение площадей пояса и стенки принимаем равным: Аf/Аw = 1.

η – коэффициент влияния формы сечения, есть функция от λусл, будет равен

для двутавра при 0 ≤ λусл ≤ 5 и Аf/Аw = 1:

η = (1.9 – 0.1 х mx) – 0.02 х (6 - mx) х λусл,

η = (1.9 – 0.1 х 3,09) – 0.02 х (6 – 3,09) х 2,43 = 1,45.

Тогда: mef = 3,09 х 1.45 = 4,48.

При mef = 4,48 и λусл = 2,43 по т.74 [7]: ϕ = 0.223 (применив двойную интерполяцию).

Тогда: Атр ≥ 108895 кг/(0,223 x 2450 кг/см² x0,9) = 212,77 см².

Определим параметры полки и стенки:

Ширину полки вf принимаем равным 1/20 х lef,y = 1/20 х 7250 = 362,5 мм.

Округляя до 50 мм получим: вf = 400 мм.

Толщину стенки tw назначим 10 мм.

hw = 480 мм. (первое приближение).

Aw = hw x tw = 1 x 48 = 48см².

Тогда: Af = (Атр – Aw)/2 = (212,77 – 48) = 164,77/2 = 82,39 см².

tf = Af/bf = 82,39/40 = 2.1 см округляя по сортаменту принимаем tf = 22 мм.

Тогда hw откорректированное:

hw = h – 2 х tf = 500 – 2 х 22 = 456 мм.

А = twxhw + 2 xtfxbf = 1 х 45,6 + 2 х 2.2 х 40 = 221,6 см² > Атр = 212,77 см².

Произведём проверку подобранного сечения:

Местная устойчивость полки:

Производим по п. 7.23 [7]:

bef/tf ≤ [bef/tf] = (0.36 + 0.1 xλусл) x (E/Ry) ^0.5, где:

bef – чистый свес полки, определяется:

bef = (bf – tw)/2 = (400 – 10)/2 = 195 мм.

bef/tf = 195/22 = 8,86

[bef/tf] = (0.36 + 0.1 x 2,43) x (2.06 х 10 ⁵/255) ^0.5= 17,14.

8,86 < 17,14 значит местная устойчивость полки выполняется.

Местная устойчивость стенки:

hw/tw ≤ [hw/tw] = λuw(усл) х (E/Ry) ^0.5, где:

λuw(усл) для двутаврового сечения при λусл > 2 и mx > 1:

λuw(усл) = 1.2 + 0.35 xλусл² = 1.2 + 0.35 x 2,43²= 3,267.

hw/tw = 456/10 = 45,6

[hw/tw] = 3,267 х (206000/245) ^0.5 = 92,857.

92,857 > 45,6 значит местная устойчивость стенки выполняется.

ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ

Сечение

Геометрические характеристики сечения

λх = lef,x/ iх = 14500/221,28 = 65,53.

λy = lef,y/ iy = 7250/102,91 = 70,45

Проверочная часть:

Ось Х-Х

Проверка общей устойчивости верхней части колонны в плоскости действия момента:

Производим по п. 5.27 [7]:

mx = exA/Wx = 51 х 221,6/4340,2 = 2,6

λх(усл) = λх х (Ry/E) ^0.5 = 65,53 х (245/206000) ^0.5 = 2,31

При Af/Aw = 88/45,6 = 1,93 > 1, тогда по т.73 [7]: