Расчёт колонны. Определение расчётных длин. Подбор сечения в верхней части колонны. Расчётная схема траверсы с эпюрами. Эпюра напряжений, страница 2

η = (1.9 – 0.1 х 2,6) – 0.02 х (6 – 2,6) х 2,31 = 1.48, тогда:

mef = 2,6 х 1.48 = 3,84 , соответственно тогда по т.74 [7]:

ϕ = 0.269.

σ = N/(Axϕ ) ≤ Ryxγc.

σ = N/(Axϕ) = 108895/(221,6 х 0.269) = 1826,78 кг/см².

Ryxγc = 2450 x 0.9 = 2205 кг/см².

2205 > 1826,78 значит проверка общей устойчивости в плоскости действия момента выполняется.

Недонапряжение: (2205 – 1827)/2205 х 100 % = 13,9 %.

Ось Y-Y

Проверка общей устойчивости верхней части колонны из плоскости действия момента:

Производим по п. 5.30 [7]:

λс = 3.14 х (E/Ry)^0.5 = 3.14 х (206000/245)^0.5 = 89,25.

mx = exA/Wx = 2,6.

α при mx = 2,6 по т. 10 [7]: α = 0.65 + 0.05 х mx = 0.65 + 0.05 х 2,6 = 0.78.

с = β/(1 + α х mx), где β при λс > λy равно 1.

Тогда: с = 1/(1 + 0.78 х 2,6) = 0,33.

При λy = 70,45 по т. 72 [7]: ϕy = 0.754.

σ = N/(с х Axϕy) ≤ Ryxγc.

σ = N/(с х Axϕy) = 108895/(0,33 х 221,6 х 0.754) = 1974,94 кг/см².

Ryxγc = 2450 x 0.9 = 2205 кг/см².

2205 > 1975 значит проверка общей устойчивости в плоскости действия момента выполняется.

Недонапряжение: (2205 – 1975)/2205 х 100 % = 10,4 %.

Проверка на гибкость:

λy = 70,45 ≤ [λ] и λх = 65,53 ≤ [λ], где:

[λ] – предельная гибкость сжатых элементов по т.19 [7]:

[λ] = 180 – 60 х α, где: α – коэффициент загрузки, определяется:

α = N/(ϕ x A x Ry x γc) = 108895/(0.269 x 221,6 x 2450 x 0.9) = 0.8.

[λ] = 180 – 60 х α = 180 – 60 x 0.8 = 132.

70,45 < 132 и 65,53 < 132 значит проверка на гибкость выполняется.

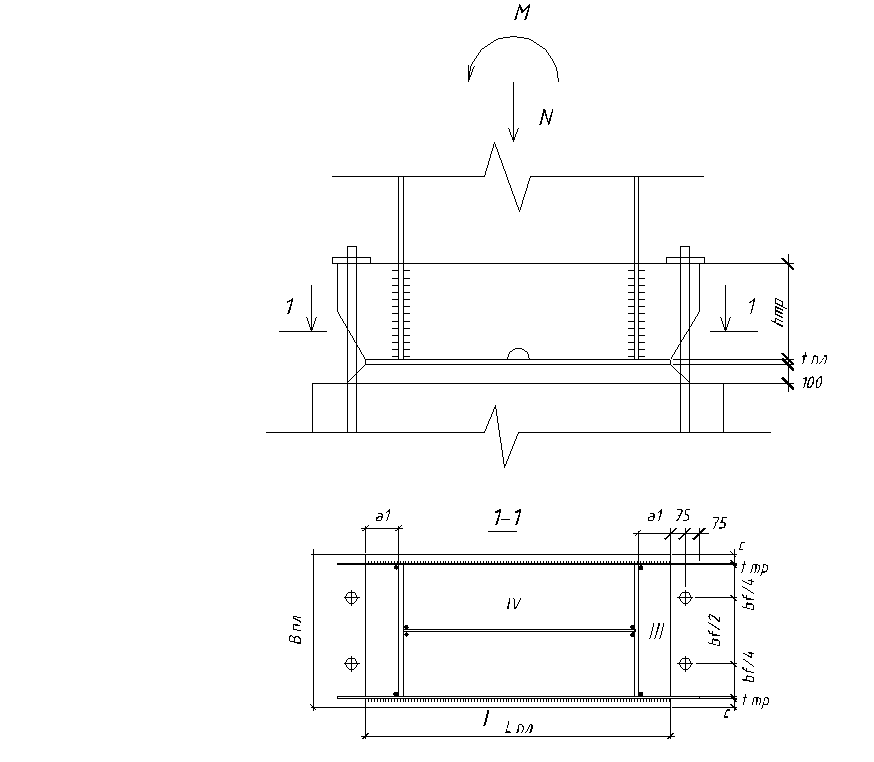РАСЧЁТ БАЗЫ КОЛОННЫ

Рис. 14 База колонны.

Принимаем бетон фундамента марки В15, с расчётным сопротивлением осевому сжатию Rb = 0.85 кН/см².

ϕв принимаем равным 1.3.

Тогда расчётное сопротивление бетона фундамента смятию:

1 2 3 4