Основные принципы метода конечных элементов

Основные принципы МКЭ

В соответствии с общими принципами метода конечных элементов [[i], [ii], [iii] и др.] исследуемая область разбивается на конечное число дискретных элементов, связанных между собой в узлах, в которых и определяется значение искомой функции . При этом ее величина в пределах площади элемента определяются с помощью аппарата интерполирования по известным функциям формы  КЭ:

.                                                      ( 3.28)

Выбор типа применяемых элементов сильно влияет на эффективность расчета. Для каждого элемента определяется соотношение, связывающее вектор узловых усилий {R}_Э и узловых перемещений {u}_Э:

                                                 (3.29)

Составление указанной системы уравнений выполняется на основе дифференциальных уравнений, описывающих то или иное явление с помощью методов вариационного исчисления [[iv]] или методов Галеркина [78]. Так на основании принципа виртуальной работы может быть записано уравнение, описывающее НДС КЭ

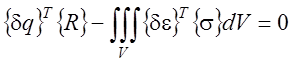,                                        ( 3.30)

где - объем элемента;  - вектор узловых перемещений;  - вектор узловых усилий;  - вектор узловых деформаций;  - вектор узловых напряжений.

Связь между напряжениями, деформациями и перемещениями обычно выражается зависимостями:

,                                                       ( 3.31)

,                                                      ( 3.32)

где  - матрица дифференцирования перемещений;  - матрица материала.

Матрица жесткости каждого элемента [k]_Э для случая решения задачи теории упругости определяется на основе известных соотношений этой теории [[v]] между деформациями и перемещениями и обобщенном законе Гука.

В результате суммирования векторов {R}_Э и матриц [k]_Э по всем элементам объекта с учетом граничных условий, задача сводится к решению системы n линейных уравнений (по числу степеней свободы КЭ модели):

,                                                      ( 3.33)

реализуемое чаще всего методом Гаусса для ленточной матрицы. Алгоритмы численного решения системы уравнений просты в реализации и отладке [67, 68 и др.]. Напряжения определяются из закона Гука и соотношений между деформациями и напряжениями  после расчета перемещений.

Необходимо отметить, что при наличии в постановке задачи геометрической и/или физической нелинейности применяют инкрементальные теории [70]. Применительно к процессу деформирования суть этих теорий заключается в том, что путь деформирования представляется в виде последовательности равновесных состояний, причем все переменные состояния считаются известными на протяжении всей истории деформирования при переходе от одного состояния к другому.

МКЭ позволяет рассматривать области произвольной конфигурации, произвольно располагать узлы сетки элементов, сгущая ее в местах ожидаемого большого градиента искомой величины, естественно формулировать граничные условия. С помощью метода КЭ могут быть рассчитаны перемещения точек среды и напряжения в ее точках в соответствии с принятой моделью материала (3.32) и геометрическими соотношениями между деформациями и перемещениями (3.31). Кроме того МКЭ позволяет решать задачи теплопроводности основанные на дифференциальном уравнении (3.24), приводимые к КЭ формулировке с помощью метода Галеркина.