Следует отметить, что функциональные связи, описанные в литературе, в большинстве случаев могут быть отнесены и к ТИ, так как случаи разрушения при лабораторных исследованиях стойкости обычно не учитывали.
Средний период стойкости инструмента в эксплуатации – условныя величина, лишенная определенного физического смысла. Она обуславливается многими процессами: изнашиванием различных видов, контактным разрушением, разрушением по различным сечениям и т.п. Прочность рабочей части инструмента влияет на его период стойкости. Так как период стойкости инструмента t является случайной величиной, необходимо оценивать ее рассеяние. Показателем рассеяния являются среднеквадратическое отклонение s, коэффициент вариации W и др. Здесь эти величины даны с индексами, показывающими, рассеяние какой величины оценивается.
Значения показателей безотказности инструмента, расчитанные по формулам типа ( ) и представленные на рисунке , являются статическими оценками, относящимися к малой выборке, т.е. к опреде-ленному числу наблюдений. Вероятностное выражение этих показателей может быть получено после нахождения теоретических законов, отражающих распределение продолжительности работы всей совокупности инструментов изучаемого типоразмера, конструкции, диапазона условий изготовления и эксплуатации (генеральной совокупности инструмента).
Показатели безотказности связаны между собой определенными зависимостями:
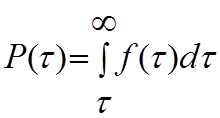 ;
; 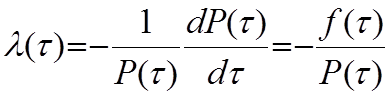 ;
;
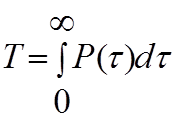 ( )
( )
Часто интенсивность отказа инструмента l(t) (см. рис. ,б) в начале работы падает (зона А), затем изменяется мало (зона Б), и в конце работы возрастает (зона В). Такой характер изменения интенсивности отказов является типичным и для других изделий. Зоны А, Б и В называют сответственно зонами приработки, нормальной эксплуатации и старения.
Исследованиями надежности различных изделий установлено, что уменьшение l(t) в зоне А связано с явлениями отбора лучших изделий за счет выбывания дефектных экземпляров, так и с физическим явленим упрочнения. В зоне Б разрушения происходят преимущественно под действием пиковых нагрузок. Появление таких нагрузок чисто случайно; их условная вероятность не зависит от момента времени, т.е. l(t) постоянно. Увеличение l(t) в конце работы вызваноизнашиванием, накоплением усталостных и других повреждений. Все эти причины повреждений справедливы и для режущего инструмента.
Случай, когда l(t) имеет максимум, тоже объясняется гибелью «слабых» и упрочнением остальных экземпляров, но не в начале работы, а в более поздний промежуток времени. Это происходит в том случае, если качество «слабых» экземпляров меньше отличается от качества остальных, чем при наличии зоны А, связанной с более грубыми технологическими дефектами. Такой случай оказался весьма распространенным для режущего инструмента со сменными многогранными пластинами (рис. ,в). Зона максимума l(t) обозначена ВА, так как l(t) здесь сначала растет, как в зоне В, а затем падает, как в зоне А.
В зависимости от качества инструмента и условий его эксплуатации кривая l(t) может иметь только некоторые зоны или даже одну из них. Так, график, характерный для инструмента высокого качества при большой однородности условий его изготовления или для легких условий эксплуатации, имеет только зоны Б и В (рис. ,г).
Закон распределения периода стойкости в значительной мере определяется вероятностью разрушения, которая в свою очередь обуславливается соотношением нагрузки на инструмент с прочностью последнего. При близких формах и размерах пластин и той же схеме их крепления закон зависит от элементов сечения среза, особенно от подачи.
Во всех ранее приведенных случаях (рис. ) установленный период стойкости ТУ=0. Этот период стойкости может существенно отличаться от нуля только в особо благоприятных условиях (высокая жесткость технологической системы, отсутствие корки, низкие значение t и S, высокое качество инструмента и т.д.). Эти условия имеют место при чистовой обработке деталей в автоматизированном производстве, когда mn/m практически равно нулю. Если ТУ>0, считают, что распределение периода стойкости имеет порог чувствительности.
Сборный инструмент представляет собой совокупность отдельных конструктивных элементов, взаимосвязанных и взаимодействующих между собой. Если бы эти элементы были независимы и отказ одного из них приводил к отказу всего инструмента, то с точки зрения теории надежности сборный инструмент представлял бы собой систему с так называемым последовательным соединением элементов. В этом случае вероятность безотказной работы инструмента:
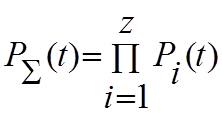 ( )
( )
где: Pi (t) – вероятность безотказной работы отдельного инструмента;
z – число элементов.
Если, например, резец имеет пять конструктивных элементов и P i (t) каждого равно 0,8, то вероятность безотказной работы резцов вцелом будет равна всего 0,327. Такой случай для режущего инструмента является довольно редким.
У сборного резца безотказность всех элементов, кроме режущей пластины, существенно выше, чем безотказность пластины. Самая низкая она у опорной пластины, но последняя обычно разрушается после поломки режущей пластины (отказ является зависимым). Поэтому во многих случаях можно рассматривать только безотказность режущей пластины, т.е. одного элемента. Остальные элементы важны лишь постольку, поскольку они влияют на прочность и износостойкость режущей пластины, виброустойчивость конструкции вцелом.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.