Функциональная зависимость на участке упрочнения и приобретенной твердостью металла

Между напряжением на участке упрочнения и приобретенной твердостью металла существует функциональная зависимость  [3]

                                    (1)

Параметры для формулы (1) приведены в таблице 1 (по данным [3])

Таблица 1 – Постоянные величины в формуле (1)

Материал	А	b
Легированная сталь
ХН77ТЮР	115	1,8
Х18Н9Т 16ГНМ	115 85	1,8 1,8
Углеродистая сталь
сталь 3	50	2
Медные сплавы
латунь Л68	35	2

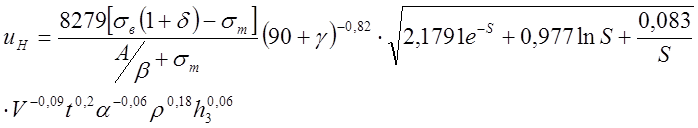
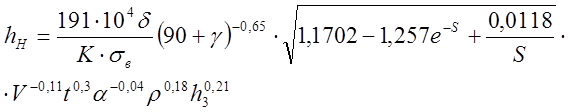
жжжжжжжжжжжжжжжжжжжжжжжжжжжж

В этой связи идут по пути упрощения исходных данных. Принимается радиус при вершине равным нулю и тогда используется выражение [8, 19, 36]

.

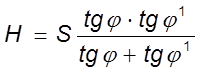Если предположить, что подача намного меньше радиуса, то можно пользоваться выражением [8,35]

.

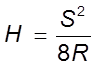При определении геометрической составляющей для случая. когда радиус при вершине r, подача S и углы j и j¹ такие, что остаточный гребешок формируется участками режущих кромок и переходной дугой между ними, рис.1.9,а, предложены формулы  А.И.Исаевым

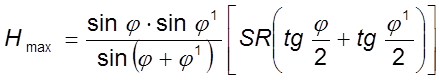
и А.Г.Сусловым

.

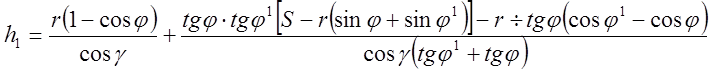Это сочетание геометрических и кинематических параметров устанавливается пр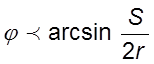и  и .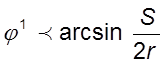

Когда геометрическая составляющая создается только дугой радиуса r, рис.1.9,г,  то ее можно определить [18] как

,

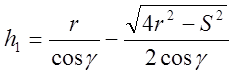или по А.И.Исаеву

.

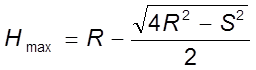Такое возможно пр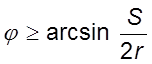и   и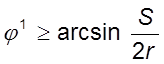

Когда шероховатость формируется радиусом при вершине и вспомогательной режущей кромкой, рис.1.9, в, то предложена формула [18]

,

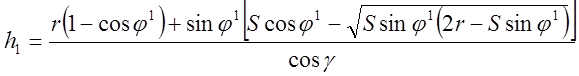или по А.И.Исаеву

Это условие наступает пр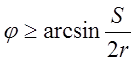и   и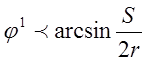

И наконец возможен и такой случай, когда остаточный гребешок формируется дугой радиуса и участком главной режущей кромки, рис.1.9, в.

Тогда формула для расчета  по [18]

,

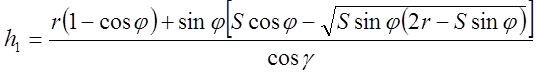а по А.И.Исаеву

Такой случай возможен пр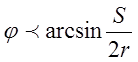и  и .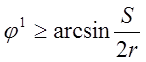

Оказалось, что имея эти формулы, достаточно сложно определить какой из них нужно воспользоваться в данном конкретном случае. При больших подачах и малом значении радиуса при вершине (или просто при условии r®0) наиболее вероятная схема формирования геометрической составляющей шероховатости представлена на рис.1.9,а. Однако при таких условиях синус в ограничивающих неравенствах (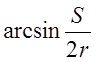) не существует. Например, при S=0,6 мм/об и  r=0,2 мм   S/2r=1,5.