







Практическая работа № 2
Тема: Теплоемкость, энтальпия, смеси идеальных газов, внутренняя энергия, работа, термодинамические процессы.
Цель работы: Закрепление знаний, полученных при теоретическом обучении, приобретение навыков в осуществлении теплотехнических расчетов.
I. Основные определения, формулы и уравнения
1. Смеси идеальных газов
Газовой смесью называется механическая смесь нескольких газов, химически не взаимодействующих между собой. Каждый из газов, входящих в смесь, называется газовым компонентом; ведет себя так, как если бы других газов в смеси не было, т.е. равномерно распределяется по всему объему смеси. Давление, которое оказывает каждый газ смеси на стенки сосуда, называюется парциальным. Основным законом для смесей идеальных газов является закон Дальтона, согласно которому давление смеси равно сумме парциальных давлений газов, образующих смесь:
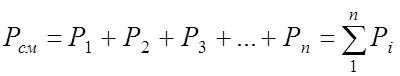
2. Внутренняя энергия
Внутренняя энергия тела представляет собой совокупность кинетической энергии движения микрочастиц, составляющих тело, и потенциальной энергии их. взаимодействия, определяемой. силами взаимного притяжения или отталкивания. Абсолютную величину внутренней энергии определить не возможно, поэтому в термодинамических расчетах вычесляется не абсолютная величина внутренней энергии, а ее изменение, т.е.
![]() или
или ![]()
где U1 и U2 - внутренняя энергия начального и конечного состояния рабочего тела (газа);
u1 и и2 - уд. внутренняя энергия начального и конечного состояния рабочего тела.
Отсюда вытекает, что изменение внутренней энергии не зависит от характера и пути процесса, а определяется состоянием рабочего тела в начале и конце процесса изменения.
Особенностью идеального газа является отсутствие в нем сил молекулярных взаимодействий, а значит и отсутсвие внутренней потенциальной энергии, т.е. Un=0 и и„ = 0. Следовательно, внутренняя энергия идеального газа:
U=Uk=f(T) unu u=uk=f(T).
З.Работа газа.
В термодинамике всякое изменение состояния рабочего тела в результате обмена энергией с окружающей средой называется процессом. При этом изменяются основные параметры рабочего тела:
P, v и Т.
Преобразования теплоты в механическую работу связано с процессом изменения состояния рабочего тела. Процессы изменения состояния газа могут быть процессами расширения и сжатия. Для произвольной массы газа М (кг) работа равна:
L = М l = Мр (v2- v1) =
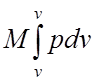 , Дж
, Дж
где l = р (v2-v1) Дж/кг - работа 1 кг газа или удельная работа.
4. Энтальпия газа,
Энтальпия - это параметр, характеризующий потенциальную энергию связи рабочего тела (газа) с окружающей средой. Энтальпия и удельная энтальпия:
I = U + pV, Дж и ii= и +pv , Дж/кг.
5. Теплоемкость.
Удельной теплоемкостью называется количество тепла, которое нужно подвести к 1 кг газа, чтобы нагреть его на 1°С в данном интервале температур.
Удельная теплоемкость бывает массовой, объeмной и киломольной. Между массовой С , объемной C и киломольной С теплоемкостями существует связь:
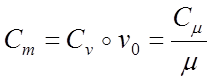 ;
; 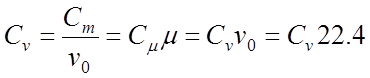
где Vo 22,4 м3/кмоль - уд. объем газа при нормальных условиях.
Массовая уд. теплоемкость газовой смеси:
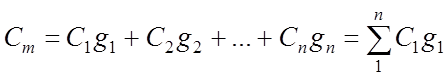
Объемная удельная теплоемкость газовой смеси:
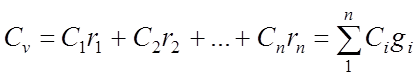
Киломольная удельная теплоемкость газовой смеси:
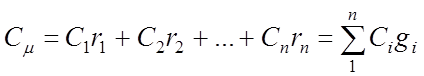
6.Уравнение для определения количества тепла
Количество тепла, отдаваемое или воспринимаемоен рабочим телом (газом) можно определить по уравнению:
Q = M Cm(t2-t1), Дж или Q = VC (t-t), Дж , где М и V - весовое или объемное количество газа, кг или м3 ;
t u t - температура газа в конце и а начале процесса ° С;
С и С - массовая и объемная средняя уд. теплоемкость газа
При tcp=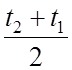 Дж/кгК или Дж/м3К
Дж/кгК или Дж/м3К
7. Первый закон термодинамики
Этот закон рассматривает взаимопревращения тепла и механической работы. По этому закону тепло превращается в механическую работу и наоборот, механическая работа в тепло в строго эквивалентных количествах. Уравнение эквивалентности тепла и работы имеет вид:
Q =L; q=l,
С учетом принципа эквивалентности тепла и работы, уравнение теплового баланса для произвольной массы газа:
Q = U + L и q =и+l= u –u +l
Решение задач II
Задача №1 (№1)
Атмосферный сухой воздух имеет следующий примерный массовый состав: g02=23,2%, gN2=76,8%.
Определить объемный состав воздуха, его газовую постоянную, кажущуюся молекулярную массу, парциальное давление кислорода и азота, если воздуха по барометру Р=101325 Па.
Определяю объемный состав воздуха:
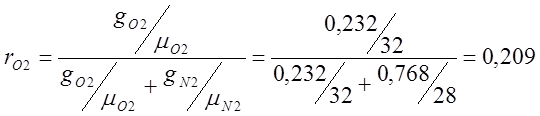 ;
;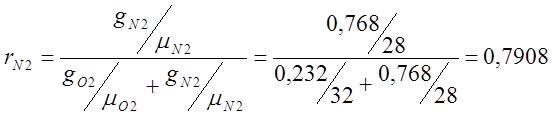 ;
;
где r – массовая доля;
m - относительная молекулярная масса;
g – объемная доля.
Определяю кажущуюся молекулярную массу воздуха:
mвозд.=mO2rO2 +mN2rN2 = 32·0,209 + 28·0,7908=6,688+22,14=28,83;
Определяю индивидуальную газовую постоянную для воздуха (R):
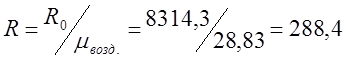
![]()
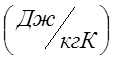 ;
;
где R0 – газовая постоянная.
Определяю парциальные давления различных газов:
PO2=Pсм· rО2 =101325·0,209=21176,9 (Па);
PN2=Pсм· rN2 =101325·0,7908 = 80127,81 (Па);
где PO2, PN2 – парциальное давление;
Pсм – давление смеси.
Задача №2 (№2)
Сосуд разделен перегородкой на 2 части, объемы которых V1=1,5 м3 и V2=1,0 м3. В первой части объемом V1 содержится СО2 при Р1=0,5 Мпа и t1=30°С; во второй части объемом V2 содержится О2 при Р2=0,2 Мпа и t2=57°С. Определить массовые и объемные доли СО2 и О2, кажущуюся молекулярную массу смеси и ее газовую постоянную после того, как перегородка будет убрана и процесс смешения закончится.
Определяю индивидуальные газовые постоянные:
Для этого определяю относительную молекулярную массу: m(СО2) =32+12=44; m(О2)=32;
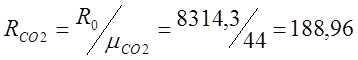
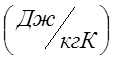 ;
;
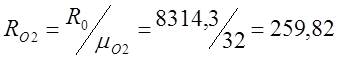
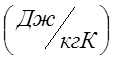 ;
;
Согласно характеристическому уравнению Клайперона, определяю массы газов:
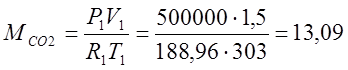 (кг);
(кг);
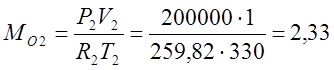 (кг);
(кг);
Определяю массовые доли:
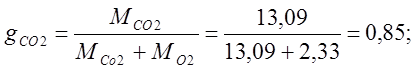
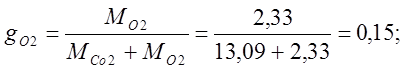
Определяю объемные доли:
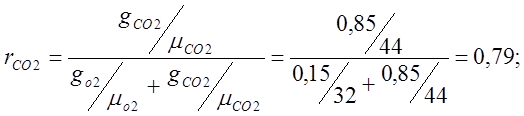
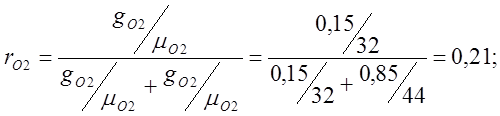
Определяю кажущуюся молекулярную массу воздуха:
mвозд.=mО2rO2 +mСО2rСО2 = 32·0,21 + 44·0,79=6,72+34,74=41,48;
Определяю индивидуальную газовую постоянную для воздуха (R):
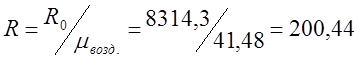
![]()
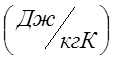 ;
;
Задача №3 (№6)
В сосуде объемом
300л находится кислород при давлении Р1=0,2 Мпа и t1=200С.
Какое количество теплоты нужно подвести, чтобы температура кислорода повысилась
до t2=3000С ? Какое давление установится при этом в сосуде ? Для
расчета принять среднюю объемную удельную теплоемкость кислорода при н.у. С02
=0,935 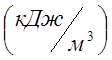
По закону Шарля определяю конечное давление процесса:
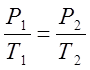 ;
; 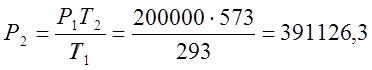 (Па);
(Па);
где Р,Т – параметры газа.
Определяю индивидуальную газовую постоянную для кислорода (R):
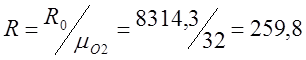
![]()
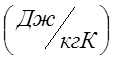 ;
;
Так как процесс изохорный то определяю количество теплоты которое нужно подвести по соответствующей формуле: Qv=M·Сcv·(T2-T1) для этого согласно характеристическому уравнению Клайперона, определяю массу газа
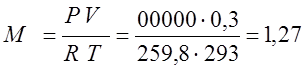 (кг); Qv=M·Сcv·(T2-T1)=1,27·935·280=332486 (Дж).
(кг); Qv=M·Сcv·(T2-T1)=1,27·935·280=332486 (Дж).
Задача №4 (№7)
Какое
количество теплоты
необходимо затратить, чтобы нагреть 2м3 воздуха при постоянном
избыточном давлении Ризб.=0,2 МПа от температуры 1000С до
температуры 5000С. Какую работу при этом совершит воздух? Для
расчета принять: давление атмосферы Рат.=0,1 Мпа, среднюю
массовую изобарную теплоемкость воздуха Сpm=1,022 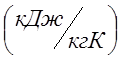 ; газовую постоянную рассчитать
имея ввиду, что кажущаяся молекулярная масса воздуха Мвозд.=29.
; газовую постоянную рассчитать
имея ввиду, что кажущаяся молекулярная масса воздуха Мвозд.=29.
Определяю индивидуальную газовую постоянную для воздуха:
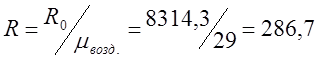
![]()
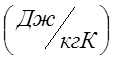 ;
;
Абсолютное давление равно сумме избыточного и атмосферного Р=Ризб.+Рат.=0,1+0,2=0,3 МПа
Согласно характеристическому уравнению Клайперона, определяю массу газа:
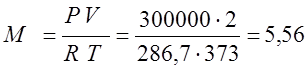 (кг);
(кг);
Так как процесс изобарный то определяю Q и L по соответствующим формулам:
по закону Гей-Люссака определяю конечный объем:
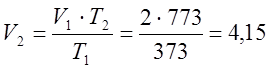 м3;
м3;
Q=M·Cpm·(T2-T1)= 5,56·1022·400=2272928 (Дж);
L=P·(V2-V1)=300000·2,15=645000 (Дж).
Задача №5 (№8)
В цилиндре находится воздух при давлении Р=0,5 Мпа и температуре t1=4000C. От воздуха отнимается теплота при Р=const так, что в конце процесса устанавливается температура t2=00C. Объем цилиндра, в котором находится воздух V1=400л.
Определить количество отнятой
теплоты, конечный объем, изменеие внутренней энегии и совершенную работу сжатия
Cpm=1,028 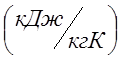 .
.
Так как процесс изобарный то по закону Гей-Люссака определяю конечный объем:
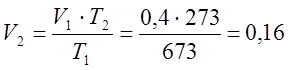 м3;
м3;
Согласно характеристическому уравнению Клайперона, определяю массу газа:
Из предыдущей задачи R=286,7 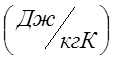
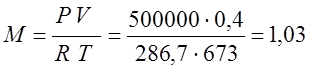 (кг);
(кг);
Определяю количество теплоты которое выделяется:
Q=M·Cpm·(T2-T1)=1,03·1028·(273-673)=-423536 (Дж);
Определяю количество затраченной работы:
L=P·(V2-V1)= 500000·(0,16-0,4)=-120000 (Дж);
Из уравнения, по которому определяется полное количество, определяю изменение количества внутренней энергии:
![]() ;
; ![]() (Дж)
(Дж)
Задача №6 (№9)
Воздух, имеющий обьем V1=0,02 м3 при давлении Р1=1,1МПа и t1=25с расширяется в цилиндре с подвижным поршнем до давления Р2=0,11Мпа. Найти конечный обьем V2, конечную температуру t2, работу, произведенную воздухом, и подведенную теплоту, если расширение в цилиндре происходит:
а) изотермически
б) адиабатно с показателем адиабаты к=1,4
в) политропно с показателем политропы n=1,3
Изотермический процес:
T1=T2=298k
P1/P2=V2/V1
V2=0,02·1,1/0,11=0,2M3
Q=L=RMT1Ln(V2/V1)=P1V1Ln(V2/V1)=1,1·106·0,02Ln(0,2/0,02)=22000Дж
Адиабатный процес:
PVk-const
V1/V2=(P2/P1)1/k
V2=V1/(P2/P1)1/k=0,02/(0,11/1,1)1/1,4=0,1036M3
T2/T1=(P2/P1)k-1/k
T2=(P2/P1)k-1/k·T1=(0,11/1,1)1,4-1/1,4·298=20,32k
Q=0
Rвоз=286,7
Сv=727,4Дж/кг·k
L=1/k-1(P1V1-P2V2) =(1/1,4-1)· (1,1·106·0,02 -0,11·106·0,1)=2,0275·106Дж
Политропный процес:
V1/V2=(P2/P1)1/n
V2=V1/(P2/P1)1/n=0,02/(0,11/1,1)1/1,3=0,118M3
T2/T1=(P2/P1)n-1/n
T2=(P2/P1)n-1/n·T1=(0,11/1,1)1,3-1/1,3·298=175k
L= 1/n-1(P1V1-P2V2)= (1/(1,3-1))· (1,1·106·0,02 -0,11·106·0,118)=30000Дж
l=L/M
Q=(k-n/k-1)·l·M=((1,4-1,3)/(1,4-1))·30000=7500Дж
Литература:
1. «Энергия», Москва, 1975.
2. Литвин А.М. «Теоретические основы теплотехники», издательство «Энергия», Москва,1969.
3. Тугунов П.И., Самсонов А.А., «Основы теплотехники, тепловые двигатели и паросиловое хозяйство», издательство «Недра», Москва, 1970.
4. Крутов В.И., «Теплотехника», издательство «Машиностроение», Москва, 1986.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.