Задание:
Определить, каким должно быть давление сжатого воздуха pM в резервуаре А, чтобы обеспечить в трубопроводе расход воды Q. Построить линии полного и пьезометрического напоров.
Расчетные данные приведены в таблице 1.
Таблица 1 – Расчетные данные.
|
Q, м3/с |
PM2, Па |
l1, м |
l2, м |
d1, м |
d2, м |
xз |
Жидкость |
Труба |
|
0,028 |
2*104 |
45 |
7,5 |
0,15 |
0,2 |
3,5 |
Вода |
Из цветных металлов тянутая новая |
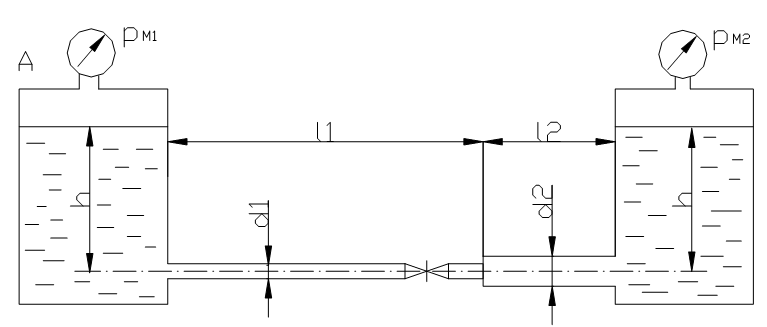
Задача №1
1. Для данного условия задачи запишем зависимость, связывающую все характеристики течения жидкости в заданной установке.
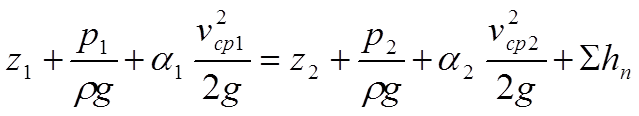 Согласно формулы [1], стр. 47, (1.55) запишем уравнение Бернулли для
потока вязкой жидкости:
Согласно формулы [1], стр. 47, (1.55) запишем уравнение Бернулли для
потока вязкой жидкости:
(1)
где z1, z2 – геометрические высоты выбраных живых сечений;
p1, p2 – давления в живых сечениях;
r - плотность жидкости;
g – ускорение свободного падения, g=9.807 м/с2;
a1, a2 - коэффициенты кориолиса для сечений 1 и 2;
vср1, vср2 – средние скорости жидкости в живых сечениях;
S hп – суммарные потери в трубопроводе.
Выбираем два живых сечения потока, нумеруем их по ходу движения жидкости: 0-0, 4-4. Выюираем плоскость сравнения 0’-0’ (она совпадает с живым сечением 0-0). Записываем уравнение Бернулли применительно к условию задачи:
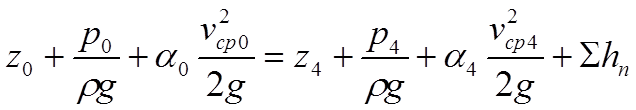
(2)
где z0 – геометрическая высота в живом сечении 0, м;
z4 – геометрическая высота в живом сечении 4, м;
p0 – давление в живом сечении 0, Па;
p4 – давление в живом сечении 4, Па;
r - плотность воды, по таблице 1.1 [2] стр.10 для 20 0С
r =1000 кг/м3;
g – ускорение свободного падения, g=9.807 м/с2;
a0 - коэффициент Кориолиса для сечения 0;
a4 - коэффициент Кориолиса для сечения 4;
vср0 – средняя скорость жидкости в живом сечении 0, м/с;
vср4 – средняя скорость жидкости в живом сечении 4, м/с;
S hп – суммарные потери в трубопроводе, м.
С учетом вышеизложеного запишем уравнение Бернулли, предварительно его упростив:
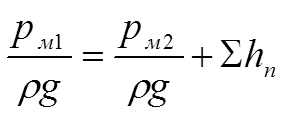
(3)
Домножим каждый член уравнения (3) на rg:
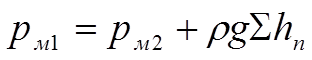
(4)
В уравнении (4) две неизвестных – суммарные потери на трение и давление в манометре 1, которое необходимо найти по условию задачи.
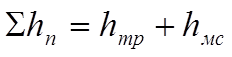 2. Рассматриваем структуру гидравлических потерь в
трубопроводе:
2. Рассматриваем структуру гидравлических потерь в
трубопроводе:
(5)
где hтр – потери на трение в трубопроводе, м;
hмс – потери напора в местных сопротивлениях, м.
2.1 Рассмотрим структуру гилравлических потерь в трубопроводе на трение:
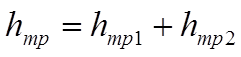
(6)
где hтр1 – потери на трение на участке l1 трубопровода, м;
hтр2 – потери на трение на участке l2 трубопровода, м.
Для нахождения потерь напора на трение необходимо установить скорость и режим движения жидкости на ииследуемом участке трубопровода. Для этого воспользуемся уравнением (1.40), [1] стр.37:
Vср=Q/S (7)
где Vср – средняя скорость движения жидкости, м/с;
Q – расход жидкости, м2/с;
S – площадь сечения трубопровода, м2.
Поскольку трубопровод имеет круглое сечение, преобразуем уравнение (7), подставляя значение площади для круга S=pd2/4:
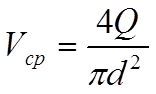
(8)
где Q – расход жидкости, м3/с;
d – диаметр трубы, м;
Определим режим движения жидкости на каждом участке трубопровода. Для этого применим критерий Рейнольдса (1.79), [1] стр.59:
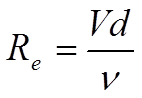
(9)
где V – скорость движения жидкости в трубопроводе, м/с;
d – даметр трубопровода, м;
v – кинематический коэффициент вязкости жидкости, м2/с.
Согласно уравнениям (8) и (9) определим скорости движения жидкости на первом и второи участках трубопровода, а также числа Рейнольдса для этих участков:
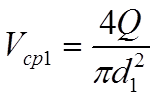
(10)
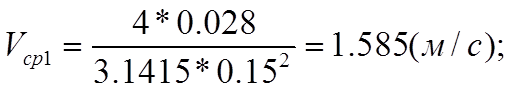
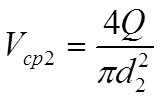
(11)
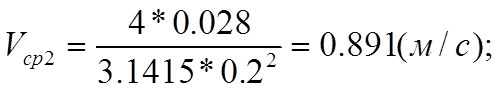
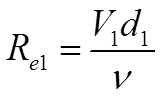
(12)
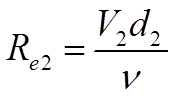
(13)
По таблице 2 [2], стр.16 определяем кинематический коэффициент вязкости для воды при 20 0С:
v=1.01*10-6 м2/с;
Определяем значение числа рейнольдса для каждого участка:
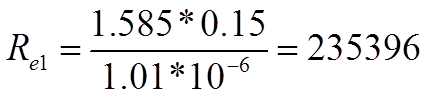
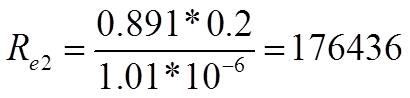
По всей длине трубопровода имеем турбулентное движение. Согласно формулы Дарси-Вейсбаха (1.59) [1] стр. 50 определяем гидравлические потери напора на трение на каждом участке трубопровода:
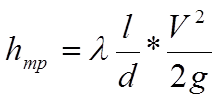
(14)
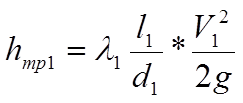
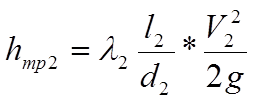 (15)
(15)
(16)
В зависимости от шероховатости и числа Рейнольдса находим коэффициент l из уравнения (14) согласно уравнения (4.45) [4], стр. 45:
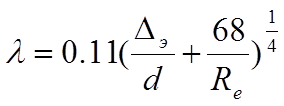
(17)
По таблице 4.4 [2], стр. 72 выбираем шероховатость трубы из цветных металлов тянутую новую: Dэ=0,005 мм.
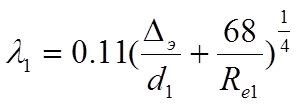
(18)
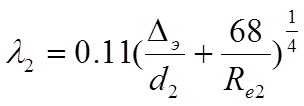
(19)
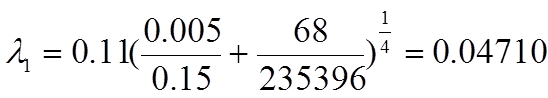
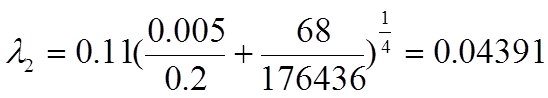
Согласно уравнений (15), (16) и (6) определяем численные значения потерь напора на трение на кождом участке и суммарные:
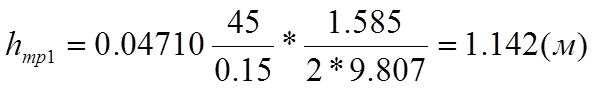
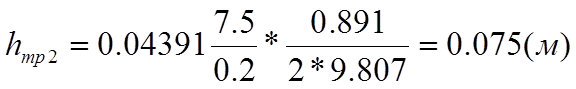
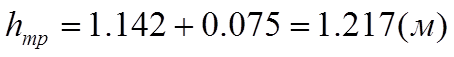
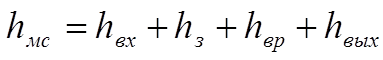 2.2 Рассмотрим структуру гидравлических потерь в
местных сопротивлениях трубопровода:
2.2 Рассмотрим структуру гидравлических потерь в
местных сопротивлениях трубопровода:
(20)
где hмс – гидравлические потери в местных сопротивлениях;
hвх – гидравлические потери при входе в требопровод;
hз - гидравлические потери в задвижке;
hвр - гидравлические потери при внезапном расширении трубопровода;
hвых - гидравлические потери при выходе трубопровода во второй резервуар.
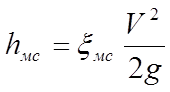 Согласно уравнения (1.57) [1], стр.49 определяем потери напора в местных сопротивлениях:
Согласно уравнения (1.57) [1], стр.49 определяем потери напора в местных сопротивлениях:
(21)
где hмс - гидравлические потери в местных сопротивлениях;
xмс – коэффициент потерь;
V – скорость течения жидкости через местное сопротивление.
Согласно уравнения (21) определяем потери напора в каждом местном сопротивлении:
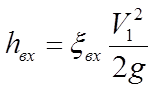
(22)
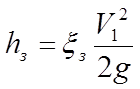
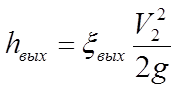
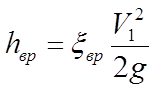 (23)
(23)
(24)
(25)
Определяем коэффициенты местных сопротивлений:
1. Вход в трубопровод:
xвх=0.5 таблица 5.2 [2], стр. 112;
2. Задвижка:
xз=3.5 по условию;
3. Выход из трубы:
xвых=1 таблица 4.17 [2], стр. 96;
4. Внезапное расширение:
В зависимости от площадей сечений трубопровода при внезапном расширении согласно [2], табл. 4.17 стр.96:
xвр=0.5(1-S1/S2) (26)
где S1 – плошадь трубопрвода до расширения;
S2 – площадь трубопровода после расширения.
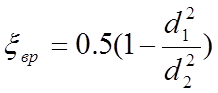 Так как
сечение трубопровода – круг, то уравнение (26) будет иметь вид:
Так как
сечение трубопровода – круг, то уравнение (26) будет иметь вид:
(27)
где d1 - диаметр трубопрвода до расширения;
d2 - диаметр трубопрвода до расширения.
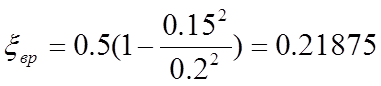
Из уравнений (22) – (25) определим численные значения потерь напора в каждом из местных сопротивлений:
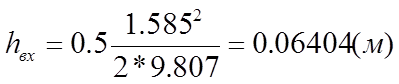
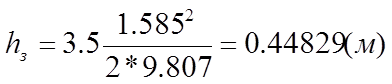
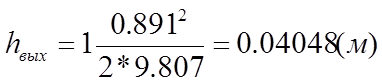
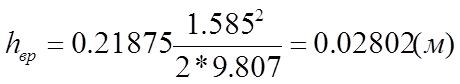
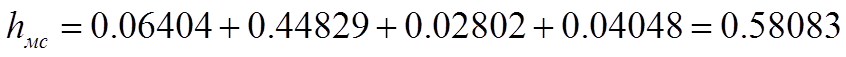 С помощью уравнения (20) определяем суммарные потери
напора в местных сопротивлениях:
С помощью уравнения (20) определяем суммарные потери
напора в местных сопротивлениях:
2.3 Согласно уравнения (5) определяем суммарные потери в трубопроводе:
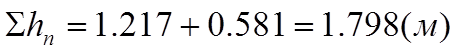
3. Из уравнения (4) определяем показания манометра в резервуаре А:
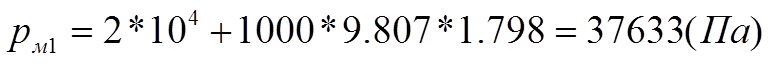
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.