Методы прямого поиска в задачах одномерной минимизации. Метод квадратичной интерполяции

1.6 Методы прямого поиска в задачах одномерной минимизации. min-? x_k+1 = x_k + t_kS_k , где S_k -направление.

Необходимо определить t_k.

(t) = f(x_k + tS_k)- найти минимум функции одной переменной (нет анализа заданной функции). Будем искать точку локального минимума, поэтому ограничимся функциями, имеющими один минимум. Больше ничего о функции неизвестно. Можно вычислить (измерить) значения функции в точках.

1. Метод квадратичной интерполяции.

Пусть функция задана на прямой, даны при этом точки a<b<c, и f a( )  f b( ), f b( )  f c( ), точка минимума в [a, c] Через эти точки проведем параболу:

g t( )  g₀  g t₁  g t₂  ²

Положим:

g a( )  f a( ),



g b( )  f b( ), , т.е. имеем 3 уравнения и 3 неизвестных g₀, g₁, g₂.

^g c( )  f c( ).

Находим g₀, g₁, g₂

 g1

] *t  argmin ( )g t    ( )min

2g₂ Рассмотрим два случая:

1)  a  t*  b  c : b b,        : t *

2)  b  t*  c  a: b b, : t *

Так поступаем до тех пор, пока точка t *не окажется в достаточно малой окрестности одной из трех точек a, b, c. После чего такую точку считаем точкой минимума.

Метод можно обобщить на случай кубических и т.д. функций, но потребуется вычислять большее количество точек.

2.  Метод дихотомии ( половинного деления.).

Если мы вычислим значения f в двух точках x₁,x₂ , то станет возможным исключение из рассмотрения некоторого множества точек, на котором гарантировано нет минимума, то есть имея измерения в двух точках можем сократить интервал поиска. 

Как лучше выбирать точки, чтобы процесс быстрее сходился?

1          1 

 В методе дихотомии предлагается x₁          ,x₂        (отрезок [0,1] ). 

2  2          2          2

    1         1  

Остается один из интервалов:0, 2  2,или2  2 ,1 . Выберем 3-й и 4-й эксперимент на -пару в середине оставшегося интервала. После n (n-четно)

n                         n

                   экспериментов min функции лежит в интервале L_n  2 ²  (1 2 ² ).

Здесь каждый раз два эксперимента, но можно один, а  в качестве другого брать один из предыдущих. 

3.  Метод «золотого» сечения.

Интервал [a,b], вычислить функцию f ,в точках t t,  .

На интервале  [a,b] расположен минимум функции.

t a F b₁(  a), _{t a F b}2 _{(  a)} , где F1 и F2 некоторые числа 0<F1<1, 0<F2<1.

Анализируем перегибы функции внутри интервала, и также, как  раньше, заменяем отрезок [a,b] на a t, или t b, . Идея метода в том чтобы после замены, необходимо было вычислить только одну точку при гарантированном уменьшении длины отрезка, т.е. b  t t  a

   F₂  F₁  F₂  1, так как b  a b  a

b  a  F b₁(  a)

  1 F₁  F₂ .(после замены отрезок уменьшится в 1/ F₂ =  b  a

В новом отрезке должно быть(по правилу «золотого» сечения): t  a     ₂

  F₂ , F₁  F₂ ,так как

t  a

F b₁(  a)     F₁

                            F₂ .

F b₂ (  a)    F₂



F1 0382.



²                                                   2

Тогда так как F₁  F₂ , F₁  F₂  1, то F₂  F₁  1 .



F₂     2     0618.

Таким образом, уменьшение интервала в 1/ F₂ =  раз достигается с помощью вычисления функции в одной новой точке (см. процедуру выполнения). После n экспериментов имеем интервал неопределенности:

L_n      _n1 ,            .

               2

В пересчете на одно измерение этот метод лучше дихотомии.

Процедура выполнения:

Рассмотрим [a,b], вычислить функцию f ,в точках t,t .

1)  f t( )  f t( )  a: t, t  t, t  a  F b₂(  a)

2)  f t( )  f t( )  a : t, t  t, t  a  F b₁(  a), b:t.

В 1) и 2) появилась только одна новая точка. И так далее, пока длина отрезка [a,b] не станет меньше заданной величины.

4 .Метод Фибоначчи.

Пусть у нас существует ограничение на количество вычисляемых точек N. Как выбирать средние точки , чтобы максимально уменьшить интервал, внутри которого лежит точка min? tk   ak  FN k 2 (bk a k )

F_{N k}

t_k ^  a_k  F^{N k 1} (b_k a _k ) , к- номер итерации.

F_{N k}

F_j - числа Фибоначчи, обладающие свойством.

Fk+2 = Fk+1+ Fk

Два первых: 1;1

Как метод Фибоначчи связан с методом «золотого» сечения?

Fk2                             3   5      Fk1                              5 1

  k        ,            k         .

F_k                                        2           F_k                                   2

То есть асимптотически один метод переходит в другой. Окончательный интервал в методе «золотого» сечения всегда на 17% больше чем в методе Фибоначчи. Если количество измерений не задано, то используется метод «золотого» сечения, если задано - то Фибоначчи.

3. Условная минимизация.

2.1 Задача нелинейного программирования. min f -?, на множестве X.

Нелинейная область: X  {x Rⁿ ,g x_i ( )  0,i  1, }- m допустимое множество.

j_i- некоторые функции. 

2.1.1 Ограничения типа равенства. рассмотрим X  {x R², (g x x₁, ₂)  0},найти min f , f R: ²  R .

x

Ïóñòü g разрешима относительно x₁, то есть x₁= (x₂).

Тогда min f  min f ( (x₂ ), x₂ )  ? 

X                    X 2

Пусть f,  - дифференцируемы. Тогда условие экстремальности:

 f   f  x₁            x₁ x₂

                           0,  , так как

1

g  g          g  g  g( (x₂),x₂)  0                           0                        

x₁ x₂ x₂                                       x₂ x₂ x₁

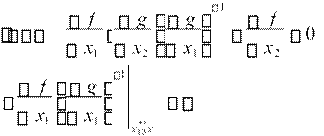
Тогда:

 f          g

x1 x1  0

 f           g

                 0 , из определения 

x2 x2

g x( ₁,x₂ )  0





Таким образом в точке минимума выполняются эти соотношения. Получить эти необходимые условия можно используя функцию Лагранжа:  F(x,)=f+g.

Тогда необходимое условие min функции f(x₁,x₂) при наличии ограничений может быть записано следующим образом:

F  f                 g

                        0

x1 x2 x2



F  f                 f

                    0

x1 x1 x1

F            g x( ₁,x₂ )  0



2.1.2 Ограничения типа неравенств.

Пусть: область, которая разрешена ограничениями

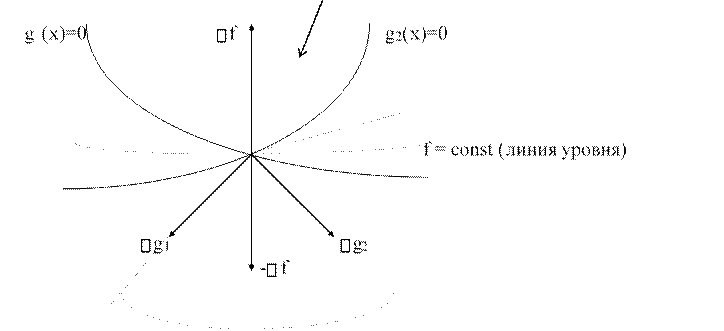1

точка минимума конус

Тогда -f представляется так:

-f = ₁g₁+₂g₂, где ₁0, ₂0.(1)

-f расположен в конусе, образованном g₁ и g₂.

(1) переписывается так:

2

f + _ig_i  0, где _i - множители Лагранжа.

i1

По рисунку _i g_i (x) = 0 (мы попадаем на границу). Тогда можно рассматривать

2

функцию Лагранжа f + _i g_i и считать стационарную точку так, будто