Можно показать, что каждой крайней точке соответствует не более n активных ограничений.
Количество ограничений в ЗЛП n+m.
Количество крайних точек не больше 
, то есть – конечно.
(c,x) -?
X = { xÎ 
: 
³ b , x ³
0} (*)
Симплекс - метод состоит из 2-х этапов:
1. Поиск крайней точки допустимого множества.
2. Перебор крайних точек с целью поиска оптимальной.
1. Поиск крайней точки допустимого множества :
Расширим пространство состояний. Введем дополнительные координаты
X = { xÎ :
- y = b , x ³ 0, y ³ 0}, (c,x)
-? (**)
Эквивалентность этих задач ((*) и
(**)) следует из того , что двойственной к обеим задачам будет : max (b,l) при 
£ с, l ³ 0.
Запишем -
y = b в виде :
1
+......+ 0 = 
+...+
-
0 +1
+...+0 = 
+...+
-
..................................................................
0 + ....... + 1
= 
+...+
- 
Переменные 
,...,
можно
рассматривать как базисные переменные, т.к. соответствующие им вектора условий
линейно независимы (вектора 
...
).
Имеем:
- переменных n+m
- уравнений m
Тогда переменные 
,...,
можно
рассматривать, как свободные переменные, которые могут принимать произвольные
значения. Как было показано выше, для того чтобы точка увеличенного
пространства 
была крайней
достаточно x = 0, т.е. 
. Т.е.
полагаем : =...: =: = 0. Если все 
= -
³ 0 , то мы получили крайнюю
точку допустимого множества. Если хотя бы один отрицателен,
то меняем систему координат (уточняется далее).
Переход к новому базису.
Обозначим полученную крайнюю точку 
=(y1=-b1,…,ym=-bm,x1=0,…,xn=0). Ей соответствует разложение по базису:
+
+...+
=
B
(1)
Разложим по базису каждый 
, j =
: =
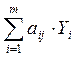
Предположим , что
для некоторого вектора , не входящего в базис , например для вектора 
, положителен хотя бы один из
коэффициентов 
.в разложении
+
+...+
=
(2)
Зададимся величиной Q>0 (пока не известной).
Умножим на нее обе части равенства (2) и вычтем результат почленно из равенства (1).
Получаем:
+
+...+
+
= B (3)
Т.о., вектор 
= (
,
, ... , 
, 0, ... , 0, 
, 0, ..., 0)
(s -место Q)
является
допустимой крайней точкой, если его компоненты неотрицательны. Т.к. Q>0, то все компоненты
вектора , в которые входят < 0 , положительны. Поэтому
надо рассмотреть только компоненты, включающие положительные . Т.е. необходимо определить
такое Q>0,при
котором для всех ,> 0 будет
³ 0 Þ 0
< Q £
.Т.е. надо Q £ 
.
Крайняя
точка не может содержать m+1 положительную компоненту, поэтому в необходимо
обнулить, по крайней мере, одну компоненту.
Положим, что Q = 
==
, т.е. r-я компонента обратится в 0.
Подставим значение в (3):
+
+...+
+..+
+…
+
=
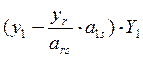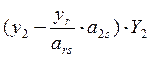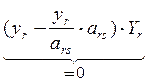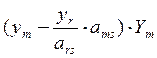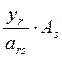B
То есть получаем новое разложение:
+...+
+...+
+
= B , которому соответствует новая крайняя
точка = (
,...,
,...,
,
0,..., 0,
, 0,...,0 ) , где 
=-×
( i =
, i¹r ), = .
Исключение одного
вектора из базиса и включение вместо него другого с помощью соответствует переходу от
одного базиса к другому с помощью метода Жордана -
- Гаусса , поэтому система векторов ......, линейно-независима
и является новым базисом.
Мы рассмотрели
переход от одной крайней точки к другой, но на первом этапе симплекс - метода
осуществляется поиск допустимой крайней точки , поэтому возможна ситуация ,
когда -< 0.Тогда надо вычислять по
формуле:
=
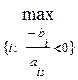
* объяснение далее в табличном методе
Мы
рассмотрели преобразование одного вектора (условий ()) по новому базису , а
надо - для всех векторов. При поиске допустимой крайней точки если хотя бы один
из < 0 , то необходимо изменить
систему координат, т.е. перейти в другую крайнюю точку.
Пусть с помощью
предыдущих рассуждений выбрали столбец s и
строку r, т.е. будем вводить в базис 
, а выводить из базиса 
Напомним :
= 
×+
×
+...+
×+...+
×-
Т.к. вводим в базис , то коэффициент
при нем должен быть 1 , а во всех других уравнениях он должен отсутствовать (=
0).
=
-
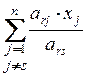+ ( изменил знак)
(4)
Подставим эту координату во все прочие ограничения , получаем:
=
+
- +
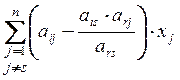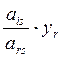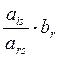, где i =, i¹r.
и (
i =, i¹r) - новые базисные переменные. За конечное число таких исключений мы
получим допустимую крайнюю точку.
Табличный метод нахождения крайней точки:
Исходные ограничения:
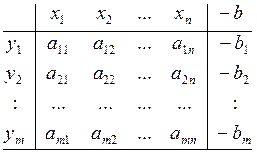
Надо , чтобы -³ 0
Как только это произойдет 
, 
(" i, j)
Получится допустимая крайняя точка.
Предположим, что одно -< 0. Сделаем одно Жорданово
исключение:
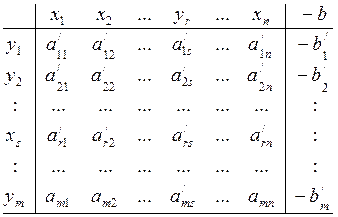
Формулы пересчета исходной таблицы:
1). r-я строка преобразуется так:
=
,
= -
, j¹s
= - - т.е. меняет знак (ниже покажем , что правые
части , которые были положительными, так положительными и остались)
(см. первую строку из (4))
2). Столбец с номером s преобразуется так :
=
, i¹r
3). Остальные элементы пересчитываются так:
=
,
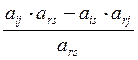i¹r, j¹s (см. вторую строку из (4))
= 
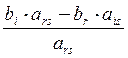, i¹r
* в
таблице , очевидно, -
Покажем, что правые части ,которые были > 0, такими и останутся.
=-
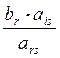
а). Пусть < 0, < 0.
Тогда 
<
-будет так, если выбирать как максимум из отрицательных.
Тогда =-= -
×(
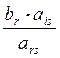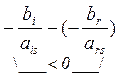) < 0
б). Пусть
<
0, > 0.
= +
×(
) << 0
Отсюда вывод :
если < 0, то < 0.
Порядок выбора , 
и 
:
( разрешающего столбца, строки и элемента)
Пусть хотя бы
один -< 0.Рассмотрим строку с
номером i. Либо все элементы этой
строки £ 0, либо хотя бы один >0.
В первом случае: допустимое множество
пусто, т.к. =
-
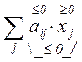£ 0.
Во втором случае: пусть > 0. Тогда
разрешающий столбец будет иметь номер s.
будем изменять от нуля до тех пор,
пока какой-нибудь из не станет = 0.
Рассмотрим отношения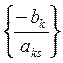 
. Ограничимся только
отрицательными. Выберем r:
= 
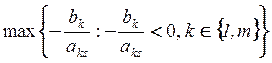
Оказывается, что с помощью такого исключения за конечное число шагов мы получим допустимую крайнюю точку.
2. Поиск оптимальной точки (перебор крайних точек допустимого множества).
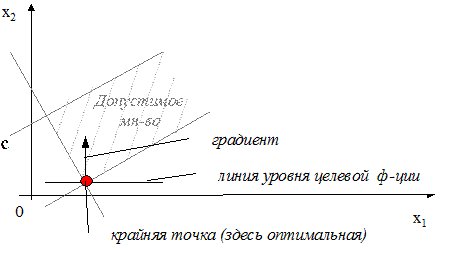
Предположим, что
допустимая крайняя точка найдена. Вектор c должен лежать в первом квадранте новой системы координат. Для этого
нужно чтобы 
³ 0.
Целевая функция f(x) =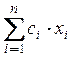 
Когда мы заменим систему
координат {
}®{
}, тогда
f= 
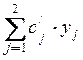-a (например,
для двумерного случая)
Стратегия: надо двигаться от одной крайней точки до другой, чтобы целевая функция уменьшалась. Это гарантирует отсутствие циклов, а, следовательно, конечное число
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
