Интерполяционный полином Ньютона. Аппроксимация зависимостей. Табулирование полинома. Клетки для разделенных разностей и коэффициентов полинома

ПРИМЕР 2

ИНТЕРПОЛЯЦИОННЫЙ ПОЛИНОМ НЬЮТОНА

Постановка задачи

Даны узловые точки Х₀, Х₁, Х₂, Х₃, Х₄ и соответствующие им известные значения аппроксимируемой функции F(x):  F₀, F₁, F₂, F₃, F₄.

Требуется :

1)  построить интерполяционный полином Ньютона четвертого порядка P₄(x).

2)  построить график P₄(x);

Пример выполнения работы

Пусть даны следующие узловые точки и соответствующие им значения аппроксимируемой функции: X₀=5,2; F₀=0,7827; X₁=6,1; F₁=5,1892; X₂=7,3; F₂=11,5522; X₃=7,9; F₃=12,8947;  X₄=8,8; F₄=11,7246.

Для наглядности значения аппроксимируемой функции были рассчитаны по формуле F(x) = x + 5 sin x.

Табулирование полинома P₄(x) для построения графика требуется выполнить на промежутке [1,252, 16,292].

Внесем в электронную таблицу исходные данные для аппроксимации:

А1¬’Аппроксимация зависимостей

А2¬’Интерполяционный полином Ньютона

А3¬’Исходные данные для аппроксимации

А4¬’Х0 B4¬’X1 C4¬’X2 D4¬’X3 E4¬’X4 F4¬’F0 G4¬’F1 H4¬’F2 I4¬’F3       J4¬’F4

А5¬5,2      B5¬6,1      C5¬7,3      D5¬7,9      E5¬8,8 

F5¬ 0,7827    G5¬ 5,1892    H5¬ 11,5522    I5¬12,8947       J5¬11,7246

Создадим электронную таблицу для расчета коэффициентов полинома P₄(x).

Заголовок таблицы:

А6¬’Полином Р4(х):

A7¬’X   B7¬’F,A0   C7¬’I,A1   D7¬’II,A2   E7¬’III,A3   F7¬’IV,A4 

Столбцы исходных данных:

A8  ¬=A5  B8  ¬=F5

A9  ¬=B5  B9  ¬=G5

A10¬=C5  B10¬=H5

A11¬=D5  B11¬=I5

A12¬=E5  B12¬=J5

Клетки для разделенных разностей и коэффициентов полинома:

С9  ¬=(B9-$B$8)/(A9-$A$8) ; копируем С9 в С10:С12 

D10¬=(C10-$C$9)/(A10-$A$9) ; копируем D10 в D11:D12

E11¬=(D11-$D$10)/(A11-$A$10) ; копируем E11 в E12

F12¬=(E12-E11)/(A12-A11)

Внесем в электронную таблицу исходные данные для табулирования P₄(x):

A13¬’Табулирование F(x), P4(x):

D13¬’Xn=  E13¬=4,0  F13¬’Xk=  G13¬=10,0  H13¬’h=  I13¬=(G13-E13)/20

A14¬’X  B14¬F(x) C14¬’P4(x)

A15¬=E13  A16¬=A15+$I$13 ; копируем A16 в A17:A35

B15¬A15^2-A15; копируем B15 в В16:В35

С15¬=$B$8+$C$9*(A15-$A$8)+$D$10*(A15-$A$8)*(A15-$A$9)+

$E$11*(A15-$A$8)*(A15-$A$9)*(A15-$A$10)+

$F$12*(A15-$A$8)*(A15-$A$9)*(A15-$A$10)*(A15-$A$11)

Копируем С15 в С16:С35

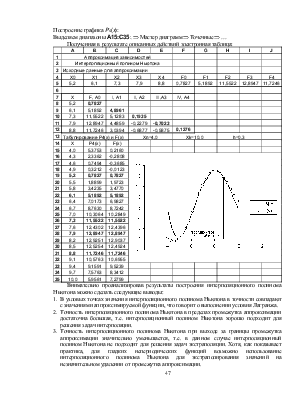
Построение графика P₄(x):

Выделяем диапазоны A15:С35; Мастер диаграммТочечные…

Полученная в результате описанных действий электронная таблица:

	A	B	C	D	E	F	G	H	I	J
1	Аппроксимация зависимостей
2	Интерполяционный полином Ньютона
3	Исходные данные для аппроксимации
4	X0	X1	X2	X3	X4	F0	F1	F2	F3	F4
5	5,2	6,1	7,3	7,9	8,8	0,7827	5,1892	11,5522	12,8947	11,7246
6
7	X	F, A0	I, A1	II, A2	III,A3	IV, A4
8	5,2	0,7827
9	6,1	5,1892	4,8961
10	7,3	11,5522	5,1283	0,1935
11	7,9	12,8947	4,4859	-0,2279	-0,7023
12	8,8	11,7246	3,0394	-0,6877	-0,5875	0,1276
13	Табулирование P4(x) и F(x)			Xn=4,0		Xk=10,0		h=0,3
14	X	P4(x)	F(x)
15	4,0	5,3753	0,2160
16	4,3	2,3362	-0,2808
17	4,6	0,7494	-0,3685
18	4,9	0,3212	-0,0123
19	5,2	0,7827	0,7827
20	5,5	1,8899	1,9723
21	5,8	3,4235	3,4770
22	6,1	5,1892	5,1892
23	6,4	7,0173	6,9827
24	6,7	8,7630	8,7242
25	7,0	10,3064	10,2849
26	7,3	11,5522	11,5522
27	7,6	12,4302	12,4396
28	7,9	12,8947	12,8947
29	8,2	12,9251	12,9037
30	8,5	12,5254	12,4924
31	8,8	11,7246	11,7246
32	9,1	10,5763	10,6955
33	9,4	9,1591	9,5239
34	9,7	7,5763	8,3412
35	10,0	5,9561	7,2799

Внимательно проанализировав результаты построения интерполяционного полинома Ньютона можно сделать следующие выводы:

1.  В узловых точках значения интерполяционного полинома Ньютона в точности совпадают с значениями аппроксимируемой функции, что говорит о выполнении условия Лагранжа.

2.  Точность интерполяционного полинома Ньютона в пределах промежутка аппроксимации достаточна большая, т.е. интерполяционный полином Ньютона хорошо подходит для решения задач интерполяции.

3.  Точность интерполяционного полинома Ньютона при выходе за границы промежутка аппроксимации значительно уменьшается, т.е. в данном случае интерполяционный полином Ньютона не подходит для решения задач экстраполяции. Хотя, как показывает практика, для гладких непериодических функций возможно использование интерполяционного полинома Ньютона для экстраполирования значений на незначительном удалении от промежутка аппроксимации.