Механизм фанерострогального станка. Структурно – кинематический анализ. Определение уравновешивающей силы методом Н.Е. Жуковского, страница 3

№ п/п	РПС,  Н	VB, м/с	, мм	, мм	, Н*м	, Н*м	, Н*м	∑МПР, Н*м
0	0	0	51	25	0	-71,4	-21	-92,4
1	0	0,96	38	19	0	-53,2	-16	-69,2
2	3500	1,65	5	2	-1375	-7	-1,7	-1383,7min
3	3500	1,44	32	15	-1200	+44,8	+12,6	-1142,6
4	0	0,08	51	25	0	+71,4	+21	92,4 max
5	0	1,35	38	19	0	+53,2	+16	69,2
6	0	1,74	5	2	0	-7	-1,7	-8,7
7	0	1,02	33	16	0	-46,2	-13,4	-59,6

Таблица №5

Выбираем масштаб:

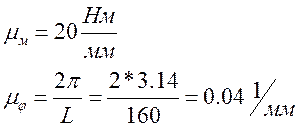
Проецируем графическим методом график изменения приведенного момента сил сопротивления, получим график работы сил сопротивлений:

 

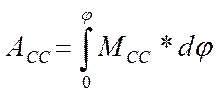
Масштаб:

= 20*0,04*50=40 Дж/мм

Графиком работы движущих сил будет прямая линия, соединяющая начало и конец графика сил сопротивлений. Приращение кинетической энергии за период установившегося движения равно избыточной работе машины:

Чтобы получить график приращения кинетической энергии  ∆Т = f(φ), необходимо алгебраически сложить ординаты графиков работ движущих сил А_ДС=f(φ) в масштабе   µ_Т=40 Дж/мм.

3.2. Приведенный момент инерции

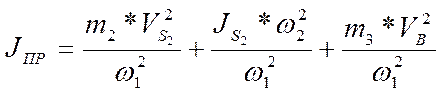
Расчет приведенных моментов инерции ведем путем заполнения таблицы.

№ п/п	, м/с	, 1/с	VB, м/с	, кг*м2	, кг*м2	, кг*м2	∑JПР, кг*м2
0	1,02	4,2	0	1,77	7,68	0	9,45
1	1,29	3,23	0,96	2,83	4,54	1,99	9,36
2	1,68	0,38	1,65	4,8	0,06	5,86	10,72
3	1,47	2,7	1,44	3,68	3,17	4,47	11,32
4	1,02	4,2	0,08	1,77	7,68	0,014	9,464
5	1,44	3,3	1,35	3,53	4,74	3,93	12,2max
6	1,71	0,45	1,74	4,97	0,09	6,52	11,58
7	1,35	2,78	1,02	3,1	3,36	2,24	8,7min

Таблица 6

Выбираем масштаб:

Строим график переменной части приведенного момента инерции.

3.3. Построение диаграммы энергомасс ∆Т = f(J_ПР), и определение момента инерции мохового колеса.

Метод расчета по диаграмме     ∆Т = f(J_ПР) принципиально точен и применяется при расчете маховых колес с относительно большой неравномерностью вращения ведущего звена.

Диаграмму эноргомасс строим методом графического исключения общей переменной  φ  из графиков   ∆Т = f(φ), и J_ПР=f(φ).

Для сохранения масштаба  проводим прямую под углом 45^о к оси Х.

Вычисляем    и :

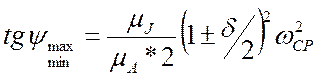
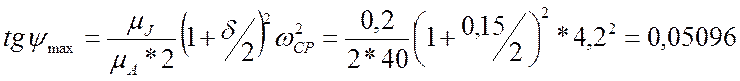
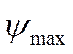= 2,917^о

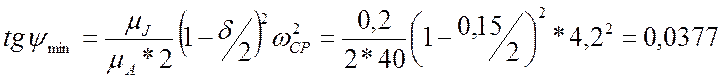
=2,1609^о

Проводим к кривой графика ∆Т = f(J_ПР) под углами  и  касательные до пересечения с осью ∆Т в точках а и в.

Момент инерции маховика:

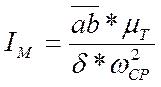
 - отрезок, отсекаемый касательными, =32 мм.

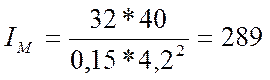кг*м²

Маховик выполняется в виде тяжелого обода, соединенного со ступицей тонким диском и устанавливается на коренной вал. Массой ступицы и диска пренебрегаем тогда:

m – масса маховика

R_CP – средний радиус обода

Принимаем  R_CP= 0,8м

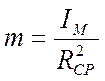
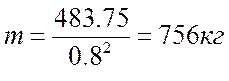
Определяем размеры обода:

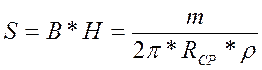
В, Н – ширина и высота обода;

 - удельная плотность.

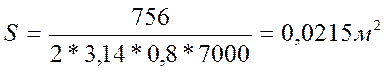
Обычно для маховиков выдерживают соотношение:

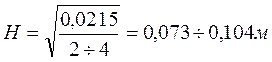
Н = 0,085 м

В = 0,253 м

4.  Анализ и синтез зубчатого механизма

4.1. Передаточные отношения

Общее передаточное отношение:

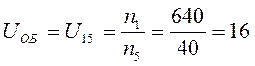
Передаточное отношение открытой передачи:

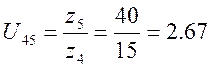
Передаточное отношение планетарного редуктора:

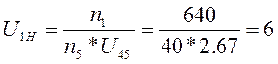
4.2 Синтез Открытой передачи

4.2.1. Определение основных размеров пары зубчатых колес.

Принимаю равносмещенное зацепление с выровненными коэффициентами относительного скольжения.

Х₁=Х₂=0,363

Делительные диаметры: