



















36
11 Проверка подшипников качения на долговечность
11.1 Расчет подшипников качения ведущего вала
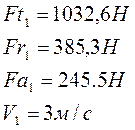
11.1.1 Определяем опорные реакции ведущего вала
Вертикальная плоскость:
![]()
![]() (92)
(92)
Определяем момент на шестерне по формуле, М1, Нмм:
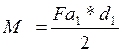 (93)
(93)
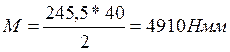
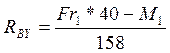 (94)
(94)
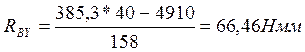
![]()
![]() (95)
(95)
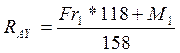 (96)
(96)
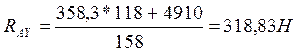
Проверка:
![]()
![]() (97)
(97)
318,83-385,3+66,46=0
37
Горизонтальная плоскость:
![]()
![]() (98)
(98)
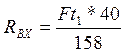 (99)
(99)
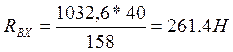
![]()
![]() (100)
(100)
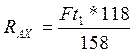 (101)
(101)
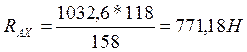
Проверка:
![]()
![]() (102)
(102)
-771,18+1032,6-261,4=0
11.1.2 Определяем суммарные реакции опор ведущего вала:
![]() (103)
(103)
![]()
![]() (104)
(104)
![]()
Наиболее нагружена опора А
39
11.1.3 Расчет эквивалентной нагрузки подшипников, Rэ, Н
RA=834,40H
Определяем эквивалентную нагрузка подшипника Rэ,H по формуле:
Rэ=(Х*V*Fr+Y*FA)*Kδ*Kт (105)
где,
Х=1 – коэффициент радиальной нагрузки,
Y=1 – коэффициент осевой нагрузки,
Так как:
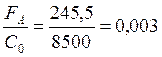 (106)
(106)
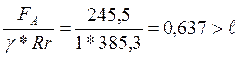 (107)
(107)
Rr1- суммарная нагрузка на первой опоре, Rr1=358,3Н
С0-статическая грузоподъемность подшипника, Н
Кδ=2 – коэффициент безопасности, т. к. характер нагрузки – переменные толчки;
Кт= 1- температурный коэффициент,
V=1 – коэффициент вращения
Rэ=(1*1*834,48+1*245,5)*1*2=1668,96 Н
Определяем долговечность подшипников на ведущем валу редуктора в часах, L10h
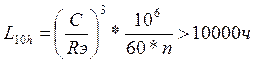 (108)
(108)
где,
С- динамическая грузоподъемность подшипника, Н (таблица В1)
Rэ- эквивалентная нагрузка подшипника, Н
n- число оборотов быстроходного (ведущего) вала, мин-1
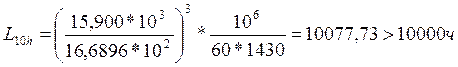
Определяем долговечность подшипников на ведущем валу редуктора в оборотах, млн. об.
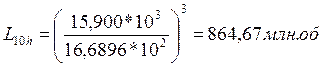
40
11.1.4 Построение эпюр изгибающих моментов ведущего вала
Вертикальная плоскость:
Под опорами изгибающий момент равен нулю;
В опасном сечении изгибающий момент равен
![]() (109)
(109)
При l1=40mm
![]()
![]() (110)
(110)
![]()
Горизонтальная плоскость:
![]() (111)
(111)
![]()
Определим изгибающие моменты Миз2, Нмм
![]() (112)
(112)
![]()
![]() (113)
(113)
![]()
41
11.2 Расчет подшипников качения промежуточного вала
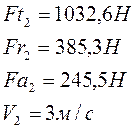
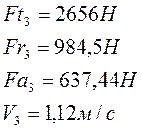
11.2.1 Определяем опорные реакции промежуточного вала
Вертикальная плоскость:
![]()
![]() (114)
(114)
Определяем момент на шестерне по формуле, М3, Нмм:
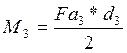 (115)
(115)
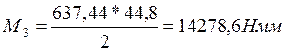
Определяем момент на колесе по формуле, М2, Нмм
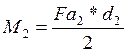 (116)
(116)
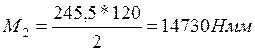
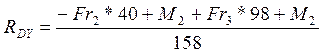 (117)
(117)
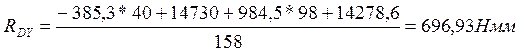
![]()
![]() (118)
(118)
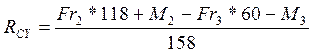 (119)
(119)
42
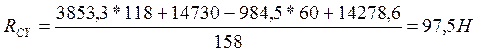
Проверка:
![]()
![]() (120)
(120)
385,3-97,5-984,5+696,93=0
Горизонтальная плоскость:
![]()
![]() (121)
(121)
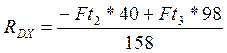 (122)
(122)
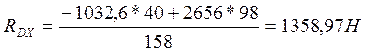
![]()
![]() (123)
(123)
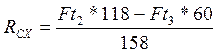 (124)
(124)
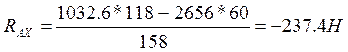
Проверка:
![]()
![]() (125)
(125)
2656-1032,6+237,4-1385,97=0
43
11.2.2 Определяем суммарные реакции опор промежуточного вала:
![]() (126)
(126)
![]()
![]() (127)
(127)
![]()
Наиболее нагружена опора D
11.2.3 Расчет эквивалентной нагрузки подшипников, Rэ, Н
RD=1551.32H
Определяем эквивалентную нагрузка подшипника Rэ,H по формуле:
Rэ=(Х*V*Fr3+Y)*Kδ*Kт (128)
где,
Х=1 – коэффициент радиальной нагрузки,
Y=1 – коэффициент осевой нагрузки,
Так как:
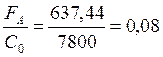 (129)
(129)
l=0,19
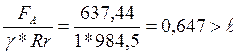 (130)
(130)
Rr1- суммарная нагрузка на первой опоре, Rr1=984,5Н
С0-статическая грузоподъемность подшипника, Н
Кδ=2 – коэффициент безопасности, т. к. характер нагрузки – переменные толчки;
Кт= 1- температурный коэффициент,
V=1 – коэффициент вращения
Rэ=(1*1*984,5+1)*1*2=1668,96 Н
Определяем долговечность подшипников на ведущем валу редуктора в часах, L10h
44
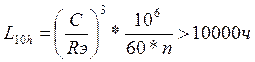 (131)
(131)
где,
С- динамическая грузоподъемность подшипника, Н (таблица В1)
Rэ- эквивалентная нагрузка подшипника, Н
n- число оборотов быстроходного (ведущего) вала, мин-1
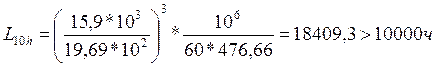
Определяем долговечность подшипников на ведущем валу редуктора в оборотах, млн. об.
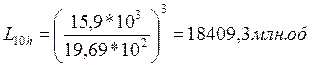
11.2.4 Построение эпюр изгибающих моментов промежуточного вала
Вертикальная плоскость:
Участок 1-1,
Под опорами изгибающий момент равен нулю при ![]() 1=0 ;
1=0 ;
В опасном сечении изгибающий момент равен
![]() (132)
(132)
При l1=98 mm
![]()
Участок 2-2
![]() (133)
(133)
![]()
Горизонтальная плоскость:
![]() (134)
(134)
![]()
Определяем изгибающие моменты Миз2, Нмм
![]() (135)
(135)
45
![]()
![]() (136)
(136)
![]()
47
11.3 Расчет подшипников качения ведомого вала
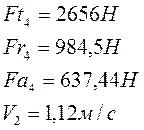
11.3.1 Определяем опорные реакции ведомого вала
Вертикальная плоскость:
![]()
![]() (137)
(137)
Определяем момент на шестерне по формуле, М4, Нмм:
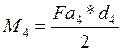 (138)
(138)
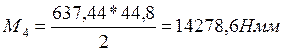
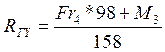 (139)
(139)
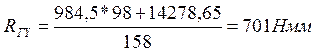
![]()
![]() (140)
(140)
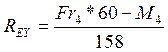 (141)
(141)
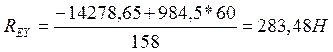
Проверка:
![]()
![]() (142)
(142)
-283,48+984,5-701=0
48
Горизонтальная плоскость:
![]()
![]() (143)
(143)
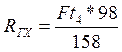 (144)
(144)
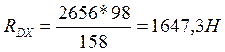
![]()
![]() (145)
(145)
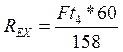 (146)
(146)
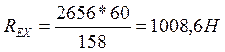
Проверка:
![]()
![]() (147)
(147)
1008,6-2656+1647,3=0
11.3.2 Определяем суммарные реакции опор ведомого вала
![]() (148)
(148)
![]()
![]() (149)
(149)
![]()
Наиболее нагружена опора Г
49
11.3.3 Расчет эквивалентной нагрузки подшипников, Rэ, Н
RГ=1790,25H
Определяем эквивалентную нагрузка подшипника Rэ,H по формуле:
Rэ=γ*Fr*Kδ*Kт (150)
где,
Так как:
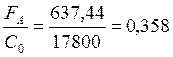 (151)
(151)
l=0,19
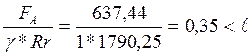 (152)
(152)
Rr1- суммарная нагрузка на первой опоре, Rr1=1790,25Н
С0-статическая грузоподъемность подшипника, Н
Кδ=2 – коэффициент безопасности, т. к. характер нагрузки – переменные толчки;
Кт= 1- температурный коэффициент,
Rэ=1*1790,25*2*1=3580,5 Н
Определяем долговечность подшипников на ведущем валу редуктора в часах, L10h
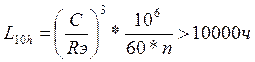 (153)
(153)
где,
С- динамическая грузоподъемность подшипника, Н (таблица В1)
Rэ- эквивалентная нагрузка подшипника, Н
n- число оборотов быстроходного (ведущего) вала, мин-1
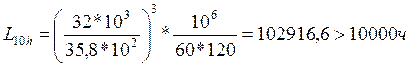
Определяем долговечность подшипников на ведущем валу редуктора в оборотах, млн. об.
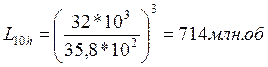
50
11.3.4 Построение эпюр изгибающих моментов ведомого вала
Вертикальная плоскость:
Участок L1
Под опорами изгибающий момент равен нулю при ![]() 1=0 ;
1=0 ;
В опасном сечении изгибающий момент равен:
![]() (154)
(154)
При l1=98 mm
![]()
Участок L2,
![]() (155)
(155)
![]()
Горизонтальная плоскость:
![]() (156)
(156)
![]()
Определяем изгибающие моменты Миз2, Нмм
![]() (157)
(157)
![]()
![]() (158)
(158)
![]()
52
12. Уточненный расчет валов.
12.1 Уточненный расчет ведомого вала.
Концентрация напряжений на ведомом валу обусловлена наличием шпоночной канавки под колесо.
Материал для изготовления тихоходного вала 40х улучшенная,
δВ=930 Н/мм2; δТ=690 Н/мм2
Определяем пределы выносливости по нормальным и касательным напряжениям по формуле:
δ-1≈0,43* δВ (159)
δ-1≈0,43*930=400 Н/мм2
![]() (160)
(160)
![]() Н/мм2
Н/мм2
Определяем запас прочности вала для опасных сечений:
По нормальным напряжениям
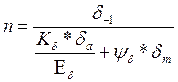 (161)
(161)
где,
δ-1 – предел выносливости на изгиб, δ-1=400 Н/мм2;
Кδ=1,72 ; Кτ=1,56 –эффективные коэффициенты концентрации напряжений, (табл 11.1);
Еδ=0,73 – коэффициент, учитывающий масштабные факторы (табл. 11.1)
ψδ=0,2 - коэффициент, учитывающий влияние постоянной составляющей цикла на усталостную прочность;
δа- амплитуда нормальных напряжений изгиба;
δm- среднее напряжение от нулевого цикла;
δа= δu=M/Wu (162)
где,
М – изгибающий момент, действующий на вал колеса, Н/мм
Wu- момент сопротивления сечения изгибу, мм3.
53
Определяем момент сопротивления сечения изгибу по формуле:
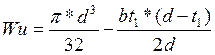 (163)
(163)
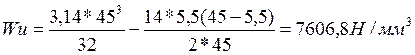
Определяем суммарный изгибающий момент в горизонтальной и вертикальной плоскостях по формуле:
![]() (164)
(164)
![]()
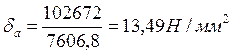
Определяем среднее напряжение от нулевого цикла,
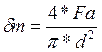 (165)
(165)
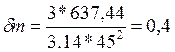
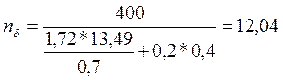
Проверка вала по касательным напряжениям nτ, по формуле:
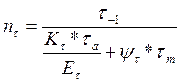 (166)
(166)
где,
τ-1=232 Н/мм2 - предел выносливости при симметричном цикле касательных напряжений;
Кτ=1,72- эффективный коэффициент концентрации касательных напряжений;
Еτ=0,63- коэффициент, учитывающий влияние масштабных факторов (табл. 11.1)
τ а – амплитуда касательных напряжений;
Момент сопротивления сечения кручению при b=14 мм, t1=5,5мм, d=45мм
54
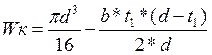 (167)
(167)
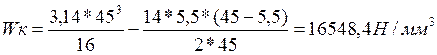
Определяем амплитуду и среднее значение касательных напряжений
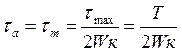 (168)
(168)
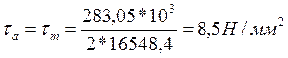
Определяем результирующий коэффициент прочности для шпоночной канавки под колесо ведомого вала, [n]>2
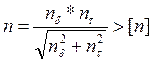 (169)
(169)
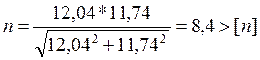
Условие прочности на выносливость шпонки под колесо на ведомом валу выполняется, [n]>2.
55
13 Выбор муфты редуктора.
Для постоянного соединения валов, а также для предохранения зубьев шестерни и колеса от перегрузок и повреждений применены две упругие втулочно-пальцевые муфты . Передаваемый первой муфтой крутящий момент Мтабл = Н · м. Диаметры соединяемых концов
dэл. двиг. = d 1вала редуктора = 30мм. Передаваемый второй муфтой, крутящий момент Мтабл = 238,5 Н · м. Диаметры соединяемых концов
d 3 валв. редуктора. = d вала смесителя = 36мм
Параметры первой муфты соединения вала электрического двигателя и ведущего вала редуктора по ГОСТ 21425-93 (приложение Ж):
При
D= мм- наружный диаметр муфты,
d= мм- диаметр отверстия для вала,
L= мм – длина муфты,
l= 58 мм – длина ступицы полумуфты
Параметры второй муфты соединения ведомого вала редуктора и вала
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.