
















8 Расчет открытой цилиндрической прямозубой передачи.
8.1 Выбор материала и расчёт допускаемых напряжений.
Для равномерного
изнашивания зубьев и лучшей их прерабатываемости твердость шестерни выбирается больше
твердости колеса: ![]() .
.
Принимаем для шестерни сталь 45 улучшенную до средней твердости НВ=240.Для колеса принимаем сталь 45,улучшенную до средней твердости НВ=220
Допускаемое напряжение на изгиб:
![]() ,
(8,1)
,
(8,1)
где ![]() предел выносливости
материала при нулевом цикле изгиба [1, стр.36].
предел выносливости
материала при нулевом цикле изгиба [1, стр.36].
Допускаемое напряжение на изгиб для шестерни:
![]()
Допускаемое напряжение на изгиб для колеса:
![]()
Принимаем число зубьев
шестерни согласно рекомендациям, так как габаритные размеры передачи не
ограничены ![]()
![]() (8,2)
(8,2)
![]()
Определяем коэффициент формы зубьев [1.таб 4,1]
Для шестерни Y=3,92 при z1=24
Для колеса Y=3,60 при z2=96
8.2 Сравнительная оценка прочности шестерни и колеса на изгиб.
Для шестерни: 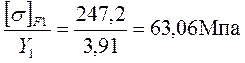
Для колеса: 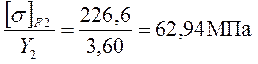
Предварительно выбираем коэффициент
ширины венца колеса при консольном расположении зубчатых колес ![]() [1.таб 4,2]; коэффициент
неравномерности нагрузки
[1.таб 4,2]; коэффициент
неравномерности нагрузки ![]() [1.таб
4,4]
[1.таб
4,4]
Определяем модуль зацепления по прочностной характеристике шестерни.
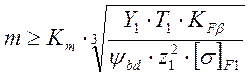 (8,3)
(8,3)
где ![]() коэффициент
модуля зацепления
коэффициент
модуля зацепления
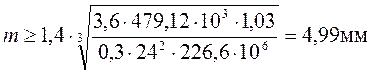
Принимаем по ГОСТу 9563-60 m=5мм
8.3 Определяем основные размеры зубчатых колёс.
Делительные диаметры колес:
![]() (8,4)
(8,4)
![]() мм
мм
![]() мм
мм
Диаметры окружностей вершин и впадин шестерни и колеса:
![]() (8,5)
(8,5)
![]()
![]()
![]() (8,6)
(8,6)
![]()
![]()
Ширины шестерни и колеса:
![]()
![]()
Определяем окружную скорость зубчатых колес
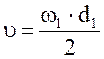 (8,7)
(8,7)
8.4 Определяем силы в зацеплении.
Окружная сила: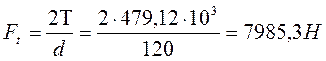
Радиальная сила:![]()
8.5 Проверочный расчёт передачи
Действительное контактное напряжение:
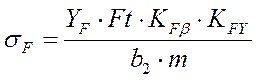 (8,8)
(8,8)
Принимаем:, ![]() [2, стр.16]
[2, стр.16]
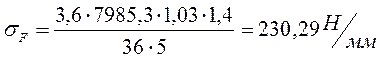
Погрешность контактного напряжения:
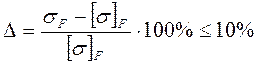 (8,9)
(8,9)
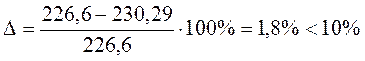 такая перегрузка допустима
такая перегрузка допустима
 |
|||||||
 |
|||||||
|
|||||||
|
|||||||
![]()
![]()
 |
 |
||||||||
![]()
 |
|||||
|
|||||
|
|||||
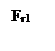
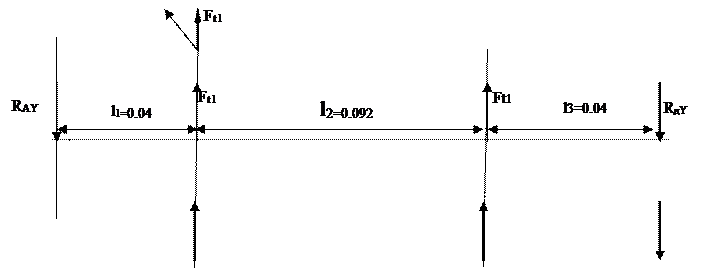 |
|
|
|
|
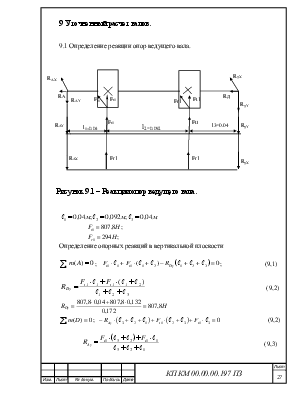
Рисунок 9.1 – Реакции опор ведущего вала.
![]()
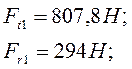
Определение опорных реакций в вертикальной плоскости
![]() ;
; ![]() ;
(9,1)
;
(9,1)
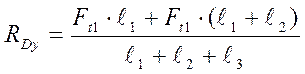 (9,2)
(9,2)
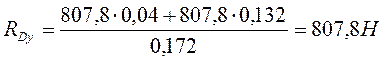
![]() ;
; ![]() (9,2)
(9,2)
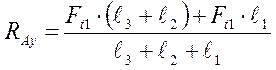 (9,3)
(9,3)
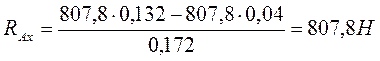
Проверка правильности решения.
![]()
![]() (9,4)
(9,4)
-807,8+807,8+807,8-807,8=0
Проверка сошлась реакции опор найдены верно
Определение опорных реакций в горизонтальной плоскости
![]() ;
; ![]() ;
;
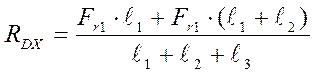 (9,5)
(9,5)
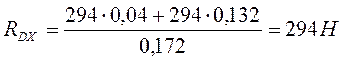
![]() ;
; ![]() (9,6)
(9,6)
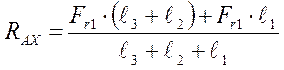 (9,7)
(9,7)
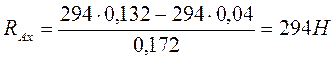
Проверка правильности решения.
![]()
![]() (9,8)
(9,8)
-294+294-294+294=0
Проверка сошлась реакции опор найдены верно
Определим суммарных реакций в опорах.
![]() ,
(9,10)
,
(9,10)
![]()
![]() (9,11)
(9,11)
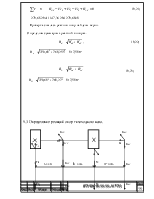
![]()
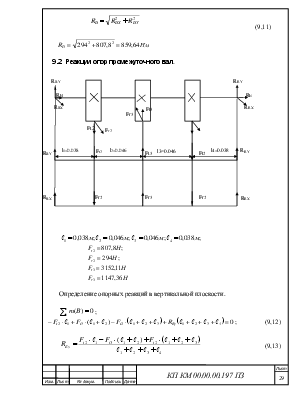
9.2 Реакции опор промежуточного вал.
|
|
||||||||||
 |
 |
||||||||||
 |
|||||||||||
![]()
![]()
 |
 |
||||||||||||||
 |
|||||||||||||||
![]()
 |
 |
 |
|||||
 |
|||||||
![]()
![]()
![]()
![]()
|
|
|
|
|
|
|||
![]()
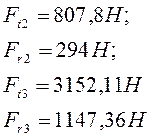
Определение опорных реакций в вертикальной плоскости.
![]() ;
; ![]() ; (9,12)
; (9,12)
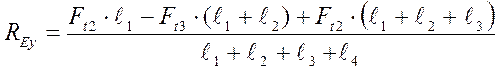 (9,13)
(9,13)

![]() ;
;
![]() (9,14)
(9,14)
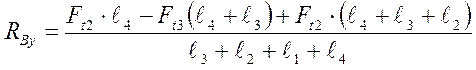 (9,15)
(9,15)
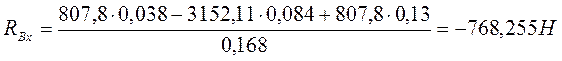
Проверка правильности решения.
![]()
![]() (9,16)
(9,16)
-768,255-807,8+3152,11-807,8-768,255=0
Проверка сошлась реакции опор найдены верно.
Определение опорных реакций в горизонтальной плоскости .
![]() ;
; ![]() ; (9,17)
; (9,17)
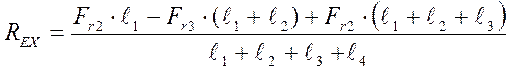 (9,18)
(9,18)
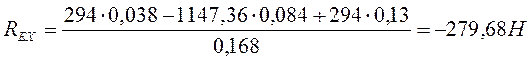
![]() ;
;
![]() (9,19)
(9,19)
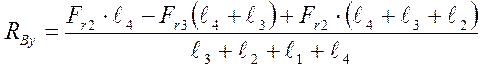 (9,20)
(9,20)
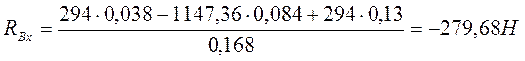
Проверка правильности решения.
![]()
![]() (9,21)
(9,21)
-279,68-294+1147,36-294-279,68=0
Проверка сошлась реакции опор найдены верно.
Определим суммарных реакций в опорах.
![]() , (9,22)
, (9,22)
![]()
![]() (9,23)
(9,23)
![]()
|
|||||||||||
|
|
||||||||||
 |
 |
||||||||||
![]()
![]()
 |
|||
 |
|||
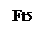
 |
|||
|
|||||||||
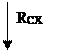 |
|||||||||
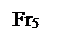
 |
|||||||
|
|||||||
|
|||||||
|
|||||||
![]()
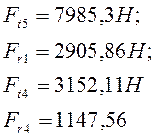
Определение опорных реакций в вертикальной плоскости.
![]() ;
; ![]() ;
(9,24)
;
(9,24)
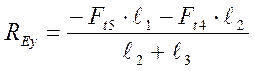 (9,25)
(9,25)
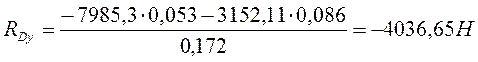
![]() ;
; ![]() (9,26)
(9,26)
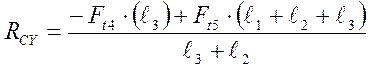 (9,27)
(9,27)
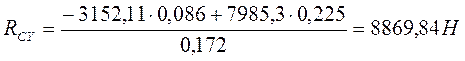
Проверка правильности решения.
![]()
![]() (9,28)
(9,28)
7985,3-8869,84-3152,11+4036,65=0
Проверка сошлась реакции опор найдены верно.
Определение опорных реакций в горизонтальной плоскости .
![]() ;
; ![]() ;
(9,29)
;
(9,29)
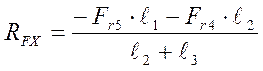 (9,30)
(9,30)
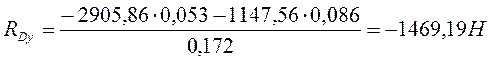
![]() ;
; ![]() (9,31)
(9,31)
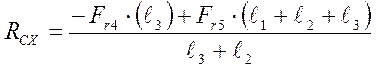 (9,32)
(9,32)
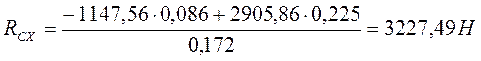
Проверка правильности решения.
![]()
![]() (9,33)
(9,33)
2905,86-3227,49-1147,56+1469,19=0
Проверка сошлась реакции опор найдены верно.
Определим суммарных реакций в опорах.
![]() ,
(9,34)
,
(9,34)
![]()
![]() (9,35)
(9,35)
![]()
|
|
||||||||||
 |
 |
||||||||||
 |
|||||||||||
![]()
![]()
![]()
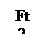
![]()
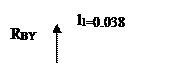 |
 |
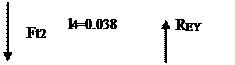 |
|||||
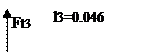 |
|||||||
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 |
 |
 |
 |
|||||||
![]()
|
|
|
|
|
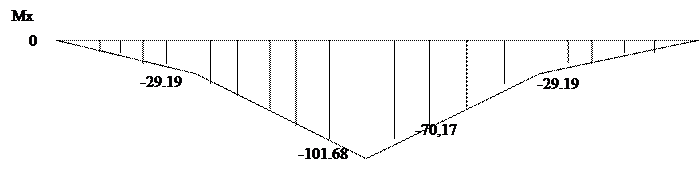 |
||||||||
|
||||||||
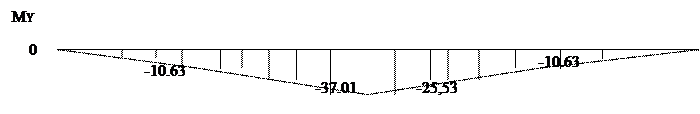 |
||||||||
|
||||||||
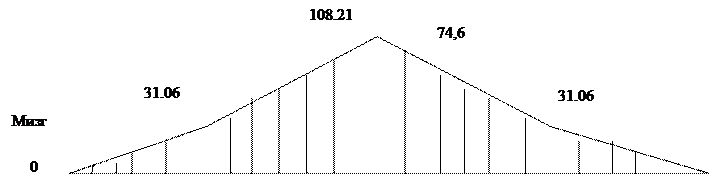 |
||||||||
|
||||||||
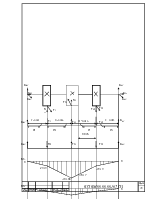
9.4 Уточненный расчет промежуточного вала.
Определение опорных реакций в вертикальной плоскости.
Сечение 1-1 при 0<z<0,038 м:
Мх=RBу*Z1; М0=0 М0,038=-29,19Н/м
Сечение 2-2 при 0<z<0,046 м:
Мх=RВу(z2+l1)-Fr2*z2; M0 =-29,19 M0.046=-101,68 Н/м
Сечение 3-3 при 0<z<0,038 м
Мх=RЕу*Z3 M0 =0 M0.038=-29,19 Н/м
Сечение 4-4 при 0<z<0,046 м
Мх=RЕу(z4+l4)-Fr2*z4; M0 =-29,19 M0.046=-101,68 Н/м
Определение опорных реакций в горизонтальной плоскости.
Сечение 1-1 при 0<z<0,038 м:
Му=RBх*Z1; М0=0 М0,038=-10,63Н/м
Сечение 2-2 при 0<z<0,046 м:
Му=RВх(z2+l1)-Fr2*z2; M0 =-10,63 M0.046=-37,01 Н/м
Сечение 3-3 при 0<z<0,038 м
Му=RЕх*Z3 M0 =0 M0.038=-10,63 Н/м
Сечение 4-4 при 0<z<0,046 м
Му=RЕх(z4+l4)-Fr2*z4; M0 =-10,63 M0.046=-37,01 Н/м
Построение эпюр изгибающих моментов.
![]() (9,36)
(9,36)
![]()
![]()
![]()
![]()
9.5 Нахождение опасного сечения.
В вертикальной плоскости.
При 0<z<0,026 м
Мх=RЕу(z4+l4)-Fr2*z4; M0 =-29,19 M0.046=-70,17 Н/м
В горизонтальной плоскости.
При 0<z<0,026 м
Му=RЕх(z4+l4)-Fr2*z4; M0 =-10,63 M0.046=-25,53 Н/м
Результирующий момент:
![]() (9,37)
(9,37)
![]()
Материал вала - сталь 45 термическая обработка-улучшение для которой ![]()
![]() (9,38)
(9,38)
![]() (9,39)
(9,39)
Расчет заключается в определении коэффициента запаса прочности для сечения A-A концентрация напряжений обусловлена посадкой подшипника с гарантированным натягом.
Определяем осевого момент сопротивления.
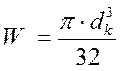 (9,40)
(9,40)
где dк – уточненный диаметр вала.
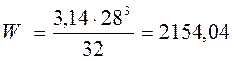 мм3
мм3
Определение амплитуда номинальных напряжений изгиба определяется по формуле:
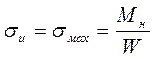 (9,41)
(9,41)
где ![]() - результирующий момент.
- результирующий момент.
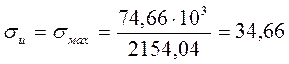 МПа
МПа
По таблице 8.7 [3] принимаем коэффициенты:
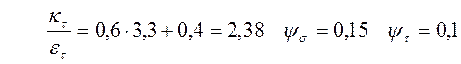
Полярный момент сопротивления.
Wp=2W=2*2154,04=4308,08 мм3
Определение амплитуды и среднее напряжение цикла касательных напряжений.
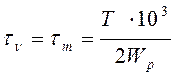 (9,42)
(9,42)
где ![]() - крутящий момент на
промежуточном валу,
- крутящий момент на
промежуточном валу, ![]() ;
;
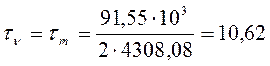 МПа
МПа
Определяем коэффициент запаса прочности по нормальным напряжениям:
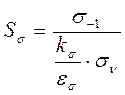 (9,43)
(9,43)
где ![]() - предел выносливости по
нормальным напряжениям
- предел выносливости по
нормальным напряжениям
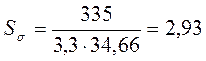
Определяем запас прочности по касательным напряжениям:
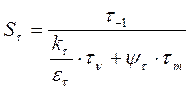 (9,44)
(9,44)
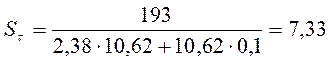
Определяем результирующий коэффициент запаса прочности:
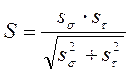 (9,45)
(9,45)
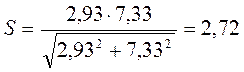
Коэффициент запаса прочности выполнился S<[S] 2,75<5
10 Расчет подшипников на долговечность.
Так как реакции в опорах
ведущего вала равны ![]() , то расчет
подшипника №207 на долговечность принимаем равную
, то расчет
подшипника №207 на долговечность принимаем равную ![]() .
.
d=35 D=72 B=17 Cr=25,5кН Co=13,7кН
Определяем эквивалентную нагрузку:
![]() (10,1)
(10,1)
где ![]() - коэффициент безопасности
принимаем равным 1,6
- коэффициент безопасности
принимаем равным 1,6
![]() - температурный коэффициент.
Принимается в зависимости от рабочей температуры подшипника. Принимаем
- температурный коэффициент.
Принимается в зависимости от рабочей температуры подшипника. Принимаем ![]()
![]() Н
Н
Определяем долговечность подшипника по формуле:
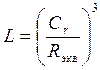 (10,2) где
(10,2) где ![]() - динамическая
грузоподъемность подшипника;
- динамическая
грузоподъемность подшипника;
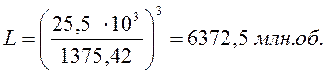
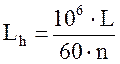 (10,3) где n – частота вращения ведущего
вала
(10,3) где n – частота вращения ведущего
вала
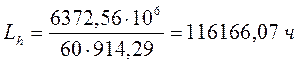
Рассчитываем на долговечность промежуточный вал подшипник №207.![]() .
.
d=35 D=72 B=17 Cr=25,5кН Co=13,7кН
Определяем эквивалентную нагрузку:
![]() (10,4)
(10,4)
где ![]() - коэффициент безопасности
принимаем равным 1,6
- коэффициент безопасности
принимаем равным 1,6
![]() - температурный коэффициент.
Принимается в зависимости от рабочей температуры подшипника. Принимаем
- температурный коэффициент.
Принимается в зависимости от рабочей температуры подшипника. Принимаем ![]()
![]() Н
Н
Определяем долговечность подшипника по формуле:
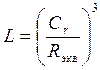 (10,5) где
(10,5) где ![]() - динамическая
грузоподъемность подшипника;
- динамическая
грузоподъемность подшипника;
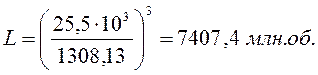
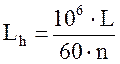 (10,6) где n – частота вращения ведущего
вала
(10,6) где n – частота вращения ведущего
вала
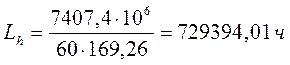
d=40 D=110 B=27 Cr=63,7кН Co=36,5кН
Определяем эквивалентную нагрузку:
![]() (10,7)
(10,7)
![]() Н
Н
Определяем долговечность подшипника по формуле:
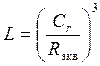 (10,8)
(10,8)
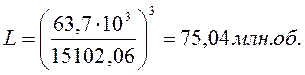
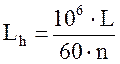 (10,9)
(10,9)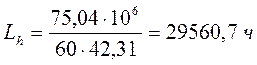
11 Выбор муфт.
Для соединения валов устанавливаем муфту упругую со звездочкой .
Расчетный вращающий момент на первом валу определяем по формуле
![]() (11,1)
(11,1)
где k – коэффициент, учитывающий условия эксплуатации, k = 1,5;
ТН1 – вращающий момент на валу, Н×м;
[Т1] - допускаемый вращающий момент, Н×м.
Тр1=1,5 × 30,85 = 46,27 Н×м
Принимаем [Т1] = 125 Н×м. ώ=210 c dотв=36мм L=144мм D=105мм
Смазка зубчатого зацепления осуществляется окунание венца зубчатого колеса в масло, заливаемое внутрь корпуса до уровня, обеспечивающего погружение колеса примерно на 10 мм.
При скорости υ=1,5 м/с рекомендуемая вязкость масла ν=20,5сСт [1, табл. 8.8]. Принимаю масло индустриальное И-20А по ГОСТ 20799-75[1, табл. 8.10].
Для смазки подшипников качения применяют тоже масло что и для смазки зубчатой пары. Смазка осуществляется разбрызгиванием масла в результате работы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.