Основные сведения об электрических цепях. Законы электрических цепей. Мощность на переменном токе. Метод комплексных амплитуд

Переменный ток обеспечивает легкость преобразования (повышение или понижение уровня напряжения в сети). Большинство сетей используют режим переменного синусоидального тока.

Рассмотрим, как ведут сябя R, L, C  в сети переменного тока.

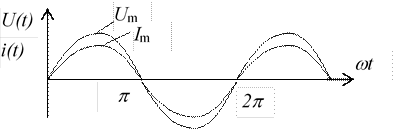
Активное сопротивление R.

                   

Если ток протекающий через активное сопротивление (резистор) меняется по закону синуса     , то напряжение на резисторе в соответствии с законом Ома    , т.е.             . Таким образом, следует отметить, что

на активном сопротивлении напряжение и ток совпадают по фазе.

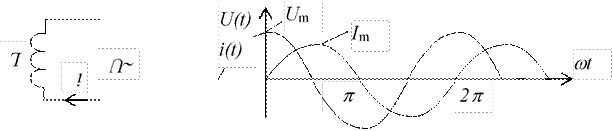
Индуктивность L.

Если ток протекающий через индуктивность L меняется по закону синуса     , то

         

  -  индуктивное сопротивление цепи переменного тока.

В идеальной индуктивности ток отстает от напряжения на 90^о.

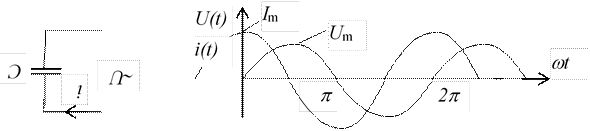
Емкость С.

Если напряжение на емкости С меняется по закону синуса         , то

                                  

В идеальной емкости ток опережает  напряжения на 90^о.

Символический метод расчета цепей переменного тока.

При включении в цепь переменного тока нескольких элементов дифференциальные уравнения по второму закону Кирхгофа имеют следующий вид

                                                   ,

,       .

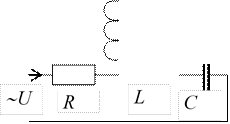
Решение данной системы дифференциальных уравнений довольно затруднительно. Решение можно существенно упростить, если перейти от дифференциальных уравнений к алгебраическим. Это можно сделать при изображении синусоидальных величин (i, u) в комплексной форме.

Изобразим напряжение  в виде вектора на комплексной плоскости.

Расположим под углом y_u относительно оси абцисс вектор U_m  , длина которого в масштабе равна амплитуде изображаемой величины.

Положительные углы будем откладывать в направлении против часовой стрелки.

Проекции вектора на вертикальную ось (ординат), ось мнимых величин в комплексной плоскости, равны мгновенному значению напряжения. 

Система векторов на комплексной плоскости называется векторной диаграммой. Поскольку все они вращаются относительно центра координат с одной и той же скоростью, относительно друг друга положение не изменяется. Поэтому векторная диаграмма изображается неподвижной в заданный момент времени, определяемый начальной фазой  какой-либо величины.

Векторные диаграммы для идеальных элементов R, L, C.

 

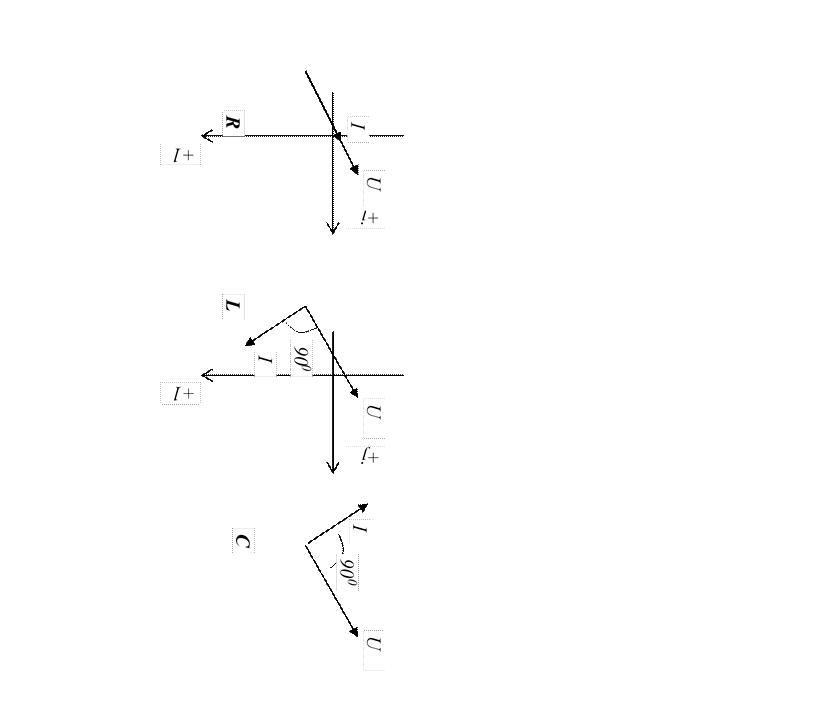
Сложение двух э.д.с. в тригонометрической форме очень трудоемко и сравнительно легко в векторной форме.

 

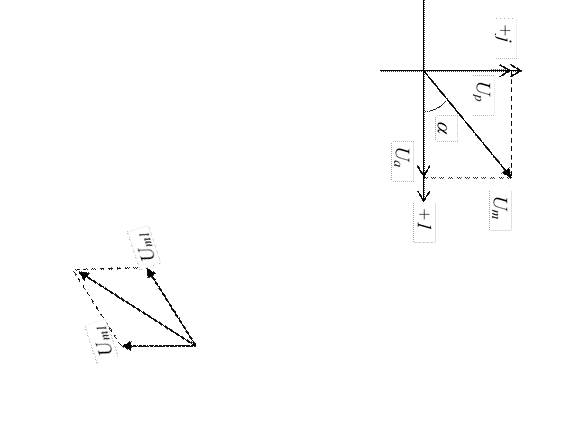Комплексные числа будем помечать точкой.

Известно, что  .

Применяют три формы записи комплексных величин:

1)   алгебраическая форма записи

2)  тригонометрическая форма записи

         

3)  показательная форма записи

    формула Эйлера.

          .

Символ j перед мнимой частью комплексного числа в алгебраической форме означает, что мнимая часть повернута по отношению к вещественной на угол 90^о в положительном направлении (против часовой стрелки). Полезно знать следующие соотношения.

.

Переходы из одной формы записи в другие.

1)     

       

2)     

                

Рассмотренная ранее система дифференциальных уравнений для цепи R, L, C в комплексном виде записывается следующим образом

Перепишем эти уравнения в другой форме.

     

Используя выражения     ,           ,  запишем

 - комплексное сопротивление цепи переменного тока

 - комплексная амплитуда напряжения

   - комплексная амплитуда тока.

    - закон Ома в комплексной форме.

Символическое изображение синусоидальных величин позволило перейти от дифференциальных уравнений к алгебраическим в комплексных величинах.

Если от амплитудных перейти к действующим значениям, то

    - закон Ома в комплексной форме.

    - первый закон Кирхгофа в комплексной форме.

    - второй закон Кирхгофа в комплексной форме.

ЛЕКЦИЯ 4

Расчет электрических цепей методом комплексных амплитуд.

Реальные элементы электрических цепей обладают индуктивностью, емкостью и активным сопротивлением. Составляя расчетные схемы и схемы замещения, мы их идеализируем, поэтому электрические схемы в самых разных задачах состоят из идеальных элементов. Соотношения между токами и напряжениями в идеальных элементах были рассмотрены ранее. Законы для цепей переменного тока те же , что и для постоянного тока.

Пример. 

Последовательное соединение элементов.

                                                   ,

,       .

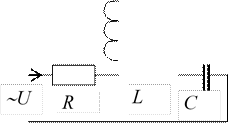
Используя символический метод, сводим решение дифференциальных уравнений к решению алгебраических уравнений.

                                                                

,        ,

,                

 = Z  - полное сопротивление,

                - реактивное сопротивление.

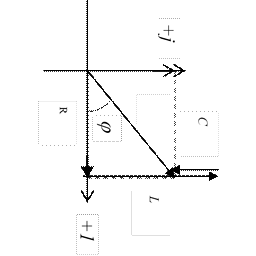
В символической форме          Z = R + j(X_L - X_C )/

Треугольник напряжений.

 

                                            .

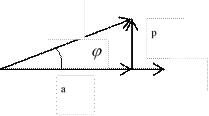Треугольник токов строится аналогично.

Треугольник сопротивлений.

 

      

          

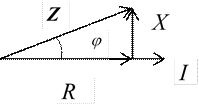Пример на последовательное соединение элементов.

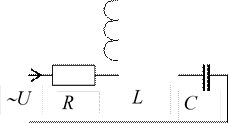                                              X_L = 20 Ом,   X_C = 10 Ом,  R = 10 Ом

U = 141 B.           I = ?

.

Ом

Параллельное соединение элементов.

 

,           ,         

Общий ток по первому закону Кирхгофа

          при параллельном соединении элементов складываются их проводимости.

Пример расчетного задания.

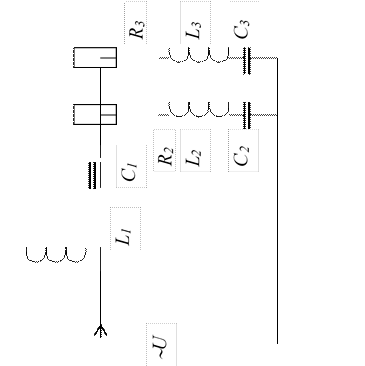Параметры всех элементов заданы. Известна w = 2pf = 314.      

Задан либо закон изменения тока в какой-либо ветви, либо напряжения на каком-либо элементе, либо значение мощности какой-либо ветви. 

Определить токи во всех ветвях, напряжения на всех элементах, мощности