Периодические несинусоидальные токи и напряжения в электрических цепях. Сглаживающий фильтр. Переходные процессы в линейных цепях с сосредоточенными параметрами

ЛЕКЦИЯ 8

Периодические несинусоидальные токи и напряжения в электрических цепях.

В промышленных сетях идеальных синусоид тока и напряжения практически не бывает, т.к. в сети постоянно присутствуют искажения, пуьсации, перекосы фаз из за несимметричной нагрузки, нелинейных элементов, таких как элементы со стальными сердечниками, выпрямительные установки, вентильные элементы, электрические дуговые печи.

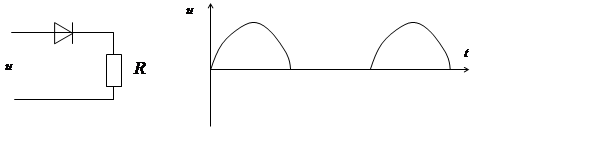Несинусоидальные токи и напряжения можно представить в виде суммы синусоидальных напряжений и токов при помощи разложения в ряд Фурье с ограничением числа членов.

В общем случае

                   

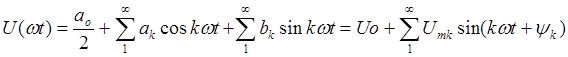
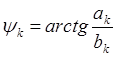
U_o - постоянная составляющая,

U_1m , U_2m -  амплитуды гармонических составляющих,

w - частота основной гармоники,

y₁  - начальные фазы гармоник.

Действующее значение напряжения или э.д.с.

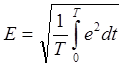
Расчет линейных цепей при несинусоидальных напряжениях .

Возможность разложения периодических несинусоидальных электрических величин в ряд Фурье позволяет свести расчет электрических цепей с линейными элементами при воздействии несинусоидальных э.д.с. к расчету цепей с постоянными и синусоидальными токами.

Мгновенные значения искомых токов и напряжений определяют на основе принципа суперпозиции путем суммирования найденных в результате расчетов постоянных и гармонических составляющих тока и напряжения.

Пример.

 

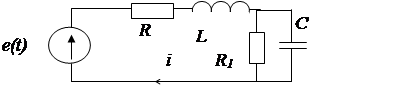Представим источник несинусоидальной э.д.с. в виде суммы постоянной и двух синусоидальных э.д.с.

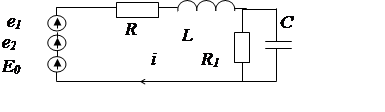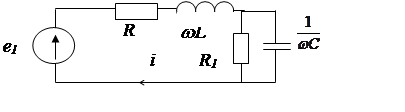
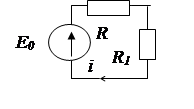а)                                       б)

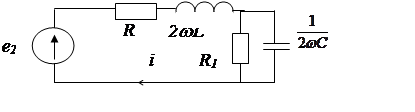в)

Для резистора R.

              

                     

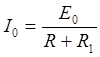
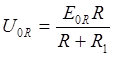
Для первой гармоники

        

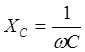
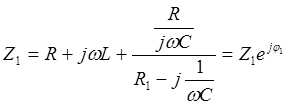
Для второй гармоники

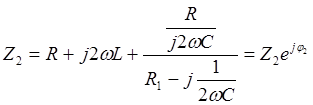
Комплексная амплитуда первой гармоники тока

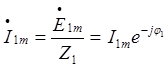
Комплексная амплитуда второй гармоники тока

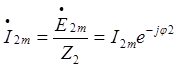
Ток в резисторе R

Электрические фильтры

Сглаживающий фильтр

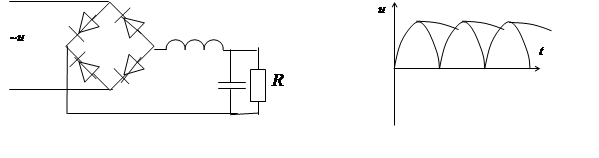Резонансные фильтры

Условие резонанса для k -ой гармоники        .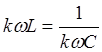

Для выделения k -ой гармоники используется явление резонанса напряжений.

Все гармоники, кроме k -ой будут подавлены. Постоянная составляющая напряжения будет отсутствовать.

Эту схему можно дополнить параллельным резонансным контуром и получим полосовой фильтр.

 

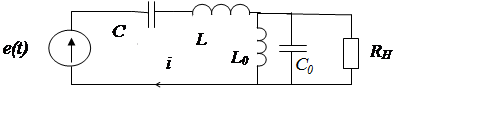Сопротивление контура L₀, C₀  для k -ой гармоники равно бесконечности. Все остальные гармоноки будут замыкаться на этот контур.

ЛЕКЦИЯ 9

Переходные процессы в линейных цепях

с сосредоточенными параметрами

Переходные процессы - процессы перехода от одного установившегося состояния к другому установившемуся состоянию. Могут быть вызваны изменением параметров элементов схемы или изменением самой схемы, то есть коммутациями.

Законы коммутации.

В природе соблюдается принцип непрерывности во времени потокосцепления индуктивности и электрического заряда емкости.

Потокосцепление скачком измениться не может  

Следствие

Ток в катушке индуктивности скачком измениться не может

В некоторых случаях это условие не выполняется

Заряд емкости скачком измениться не может      

Следствие

Напряжение на емкости скачком измениться не может

В некоторых случаях это условие не выполняется

На основании законов коммутации определяются начальные условия при расчете переходных процессов.

Классический метод расчета переходных процессов.

Анализ переходных процессов в линейных цепях с сосредоточенными параметрами сводится к решению обыкновенных линейных неоднородных дифференциальных уравнений, выражающих законы Кирхгофа. Пример был рассмотрен ранее.

Пример. Включение цепи R, L.

 

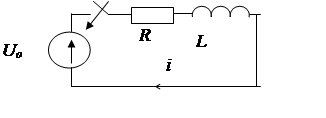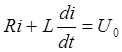
Из курса высшей математики известно, что общее решение такого уравнения может быть найдено методом наложения принужденного и свободного режимов.

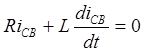             ,     где 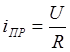    - ток принужденного режима при 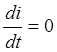 или частное решение неоднородного уравнения,

       -  ток свободного режима или общее решение однородного уравнения (с нулевой правой частью).

В общем случае

   - число слагаемых зависит от порядка уравнения.

Свободные процессы исследуются с целью определения устойчивости системы. В устойчивой системе процессы должны затухать.

Принужденный и свободный процессы в сумме определяют процессы, которые называются переходными, т.е. осуществляется переход от одного установившегося режима к другому установившемуся режиму.

Рассмотрим подробнее переходный процесс при включении цепочки R, L  на постоянное напряжение.

До коммутации (до включения) ток в цепи отсутствовал  . На основании следствия из законов коммутации можем записать

, т.е. ток в индуктивности в первый момент после коммутации равен току до коммутации. В нашем примере ток равен 0.

После коммутации переходный процесс описывается дифференциальным уравнением

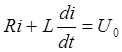
Решение ищем в виде                     

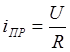  - ток принужденного режима при .

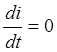Свободный процесс описывается уравнением

,    

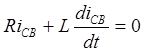Решение этого уравнения             , где k - корень характеристического уравнения   

                     

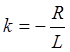
А  - постоянная интегрирования, определяемая из начальных условий при t = 0.

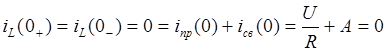,  учитывая   .

Отсюда    .

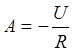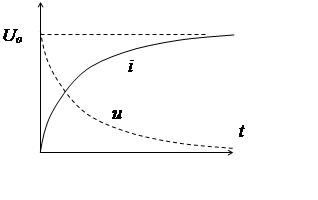Решение

    

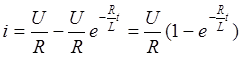
Напряжение на R

    

Напряжение на L

  

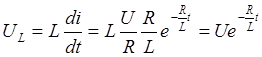
Шунтирование цепочки R, L.

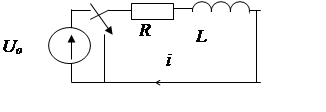Цепочка R,L отключается от источника постоянного напряжения