Частотные характеристики элементов. Идеальное и индуктивное активное сопротивление. Резонанс напряжений в цепях переменного тока. Волновое сопротивление контура

ЛЕКЦИЯ 5

Частотные характеристики элементов.

Идеальное активное сопротивление от частоты не зависит.

R = const

Индуктивное сопротивление линейно зависит от частоты

 

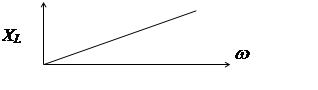                                                                                   X_L = jwL

Емкостное сопротивление зависит от частоты по гиперболическому закону

			w

 

XС

                                                                                   X_С = -j

Резонанс напряжений в цепях переменного тока.

 

.

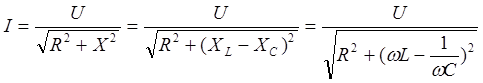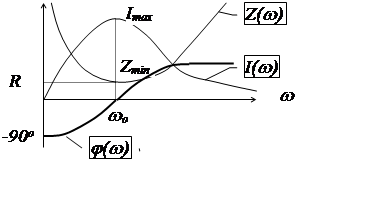
Знаменатель данного выражения есть комплексное сопротивление, модуль которого зависит от частоты. При достижении некоторой частоты реактивная составляющая сопротивления исчезает, модуль сопротивления становится  минимальным, ток в данной схеме возрастает до максимального значения, причем вектор тока совпадает с вектором напряжения.

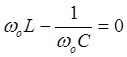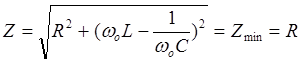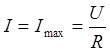,    ,  ,  j= 0.

Такое явление называется резонансом напряжений, т.к. при больших токах напряжение на элементах схемы могут достигать больших значений.

      ,    ,        ,     

 

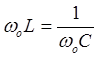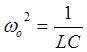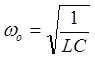
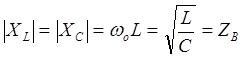  - волновое сопротивление контура.

Отношение напряжения на индуктивности или емкости к напряжению на входе в режиме резонанса называется добротностью контура.

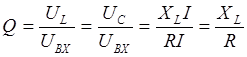
Добротность контура в лучших катушках индуктивности может достигать сотен единиц.

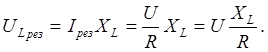
При   >>  R  напряжение на индуктивности (или емкости) может быть гораздо больше напряжения на входе, что широко используется в радиотехнике.

Резонанс токов.

Резонанс токов может возникнуть при параллельном соединении реактивных элементов в цепях переменного тока.

 

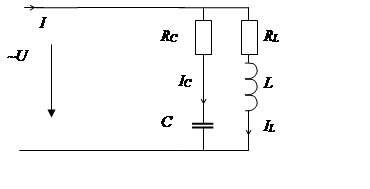
Проводимость ветви с емкостью

                      

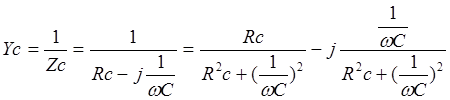
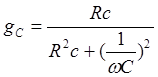
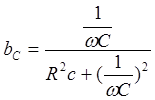
Аналогичные преобразования проделаем для ветви с индуктивностью и получим

 ,             

     .

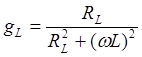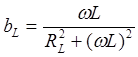
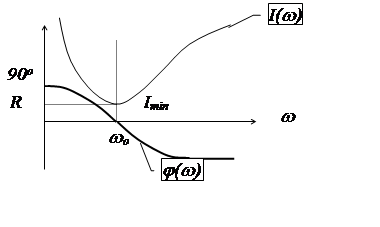
Как видно из полученных выражений, проводимости ветвей с индуктивностью и емкостью зависят от частоты, причем имеют реактивные составляющие имеют разные знаки. Следовательно, при определенной частоте, называемой резонансной, реактивные составляющие проводимости могут сравняться по модулю и суммарная проводимость будет минимальной. Общее сопротивление при этом становится максимальным, общий  ток минимальным, вектор тока совпадает с вектором напряжения. Такое явление называется резонансом токов.

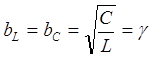  - волновая проводимость.

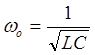,         j = 0 ,       cosj= 1.

При  g<< b_L  ток в ветви с индуктивностью гораздо больше общего тока, поэтому такое явление называется резонансом токов. Широко используется в силовых сетях промышленных предприятий для компенсации реактивной мощности.

Мощность в цепях переменного тока.

В цепи с резистором мгновенные значения мощности

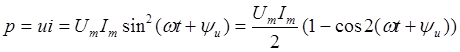
Действующее значение мощности

                                                                               

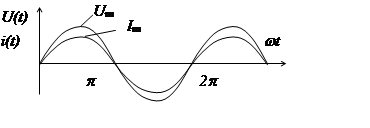
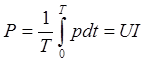
U = IR       P = I²R 

 

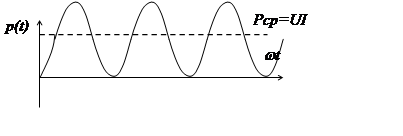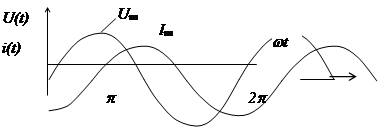
Мощность в цепи с идеальной катушкой индуктивности

, то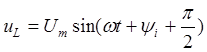           

 

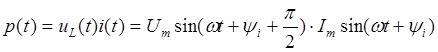
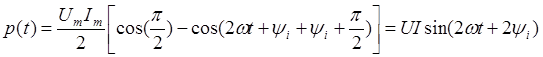
В первой четверти периода энергия от источника переходит к приемнику и запасается в индуктивности в виде энергии магнитного поля.

Во второй четверти наоборот, энергия магнитного поля возвращается источнику.

Активная мощность равна 0. Реактивная мощность Qопределяется выражением         

Q = U_LI = I²X_L.

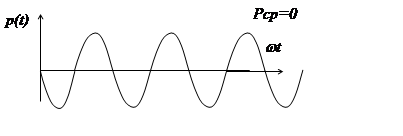
Аналогичные выкладки можно проделать для цепи с идеальным конденсатором       

P_CP = 0          Q = U_CI = I²X_C.

Рассмотрим реальную катушку индуктивности, но без межвитковой емкости