Эксперементальное исследование гидравлического прыжка, страница 2

, ./3/

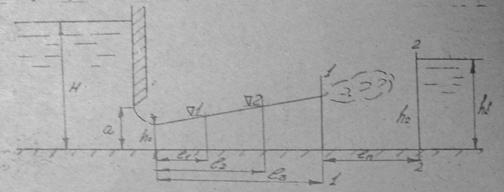
            Если , то переход потока из бурного состояния в спокойное осуществляется посредством прыжка-волны, представляющего собой ряд постепенно затухающих волн, после которых устанавливается глубина h2, при этом параметр кинетичности пред прыжком 1,5<. Рассмотрим совершенный прыжок.

Уравнение совершенного гидравлического прыжка для потока в призматическом русле с плавноизменяющимся движением и с весьма малым прямым уклоном имеет вид:

, /4/

Где      Q – расход жидкости,

 - коэффициент Буссинеска,

 - площади живых сечений перед и за прыжком,

 - глубины погружения центров тяжести живых сечений.

            Левая часть уравнения /4/ есть функция глубины а правая -. Уравнения такого типа называются в математике симметричными, а их корни сопряженными. Поэтому глубины   и называются сопряженными глубинами.

            Сопряженные глубины гидравлического прыжка в русле прямоугольного сечения определяются по формулам:

,

.     /5/

            На практике большой интерес представляет вопрос о длине гидравлического прыжка. Приведем наиболее распространенные формулы:

Формула Павловского

                /6/

Формула Пикалова

                  /7/