Статическим методом находят натяжение неподвижных поверхностей, образованных задолго до начала опыта и находящихся в равновесии с объёмом жидкости. К этому методу относится метод капиллярного поднятия или опускания жидкости. Это равновесие описывается уравнением Жюрена:
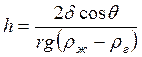 , где h – высота капиллярного поднятия или
опускания жидкости;
, где h – высота капиллярного поднятия или
опускания жидкости;
r – радиус капилляра;
q - угол смачивания, который для воды и многих органических жидкостей равен нулю.
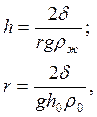
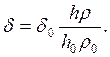
Динамические методы (метод колеблющийся струи и капиллярных волн) позволяет определить только неравновесные значения поверхностного натяжения.
Метод максимального давления:
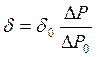 , где DР
, где DР![]() -
наибольшее давление в пузырьке чистой воды;
-
наибольшее давление в пузырьке чистой воды;
DР – давление в пузырьке исследуемой жидкости.
Капельный (сталагмометрический):
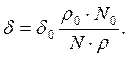
N – число капель исследуемого раствора.
3. Порядок выполнения работы.
1. Готовим четыре раствора объёмом 25 мл путём последовательного разбавления в два раза.
Исходный раствор – 10 % - ный раствор изопропилового спирта,
![]()
2. С помощью сталагмометра измеряем поверхностные натяжения сначала чистой воды, затем исследуемых растворов, начиная с самого разбавленного.
Данные сводим в таблицу:
|
Проба |
Число капель |
|||
|
|
|
|
|
|
Вода |
20 |
21 |
21 |
20,66 |
|
4 |
22 |
22 |
22 |
22,00 |
|
3 |
23 |
23 |
22 |
22,66 |
|
2 |
25 |
26 |
26 |
25,66 |
|
1 |
31 |
31 |
31 |
31,00 |
|
спирт |
39 |
39 |
40 |
39,33 |
![]() капли,
капли,
![]() - для
чистой воды при температуре Т =20
- для
чистой воды при температуре Т =20![]() ,
,
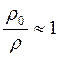 ,
,
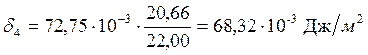 ;
;
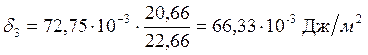 ;
;
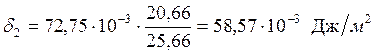 ;
;
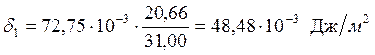 ;
;
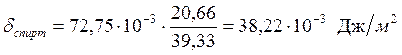
![]() .3.
Рассчитываем концентрации исследуемых растворов:
.3.
Рассчитываем концентрации исследуемых растворов:
![]() %,
%,
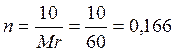 моль,
моль,
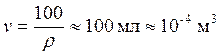 ,
,
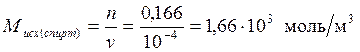 ,
,
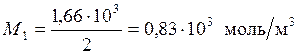 ,
,
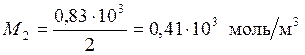 ,
,
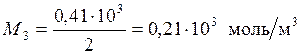 ,
,
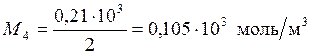 .
.
4. Строим график изотермы поверхностного натяжения d = f(C).
Проба |
|
|
М, |
|
Вода |
20,66 |
72,75 |
0,000 |
|
4 |
22,00 |
68,32 |
0,105 |
|
3 |
22,66 |
66,33 |
0,210 |
|
2 |
25,66 |
58,57 |
0,410 |
|
1 |
31,00 |
48,48 |
0,830 |
|
спирт |
39,33 |
38,22 |
1,66 |
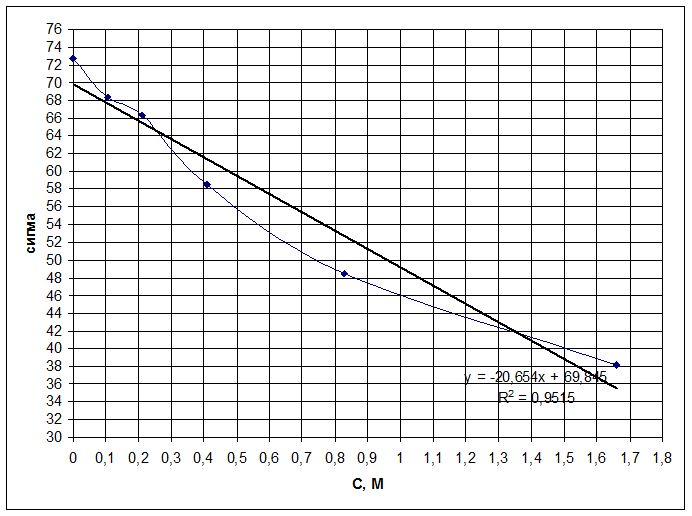
![]() 5. Вычисляем постоянные
уравнения Шишковского. Для этого, начиная с
5. Вычисляем постоянные
уравнения Шишковского. Для этого, начиная с ![]() ,
разделим график на разные ординаты:
,
разделим график на разные ординаты:
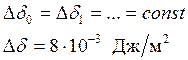 .
.
|
Номер опыта |
|
М, |
|
1 |
72,75 |
0,000 |
|
2 |
64,75 |
0,230 |
|
3 |
56,75 |
0,440 |
|
4 |
48,75 |
0,770 |
|
5 |
40,75 |
1,460 |
|
6 |
32,75 |
1,796 |
Снимаем с графика
концентрации через каждые D![]() .
Считаем среднее значение константы
.
Считаем среднее значение константы ![]() по
формуле:
по
формуле:
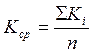 , где
, где 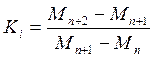 ;
;
n – число констант.
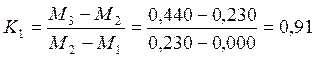 ,
,
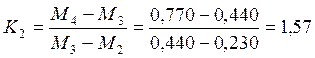 ,
,
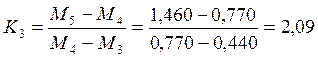 ,
,
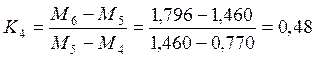
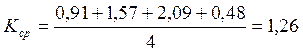 .
.
Теперь находим постоянные Шишковского a и b:
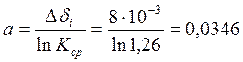
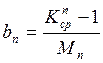
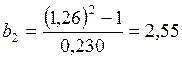
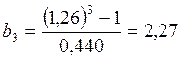
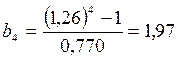
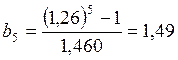
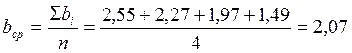
6. Вычисляем удельную адсорбцию ПАВ, используя метод графического дифференцирования по уравнению изотермы адсорбции Гиббса:
|
Y, м * |
М, |
|
Г, |
|
0,00 |
0 |
72,75 |
0 |
|
4,75 |
0,105 |
68,32 |
1,95 |
|
9,09 |
0,21 |
66,33 |
3,73 |
|
15,90 |
0,41 |
58,57 |
6,53 |
|
30,15 |
0,83 |
48,48 |
12,38 |
|
37,09 |
1,66 |
38,22 |
15,2 |
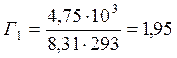
![]() ;
;
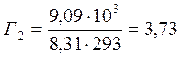
![]() ;
;
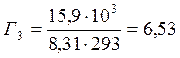
![]() ;
;
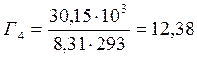
![]() ;
;
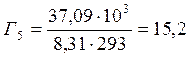
![]() ;
;
![]() 7. Определяем предельное
значение адсорбции ПАВ
7. Определяем предельное
значение адсорбции ПАВ ![]() :
:
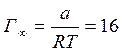
![]() ;
;
площадь одной молекулы:
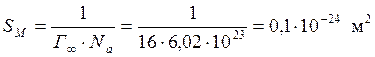 ;
;
длина одной молекулы:
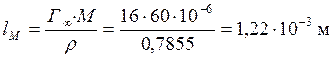 .
.
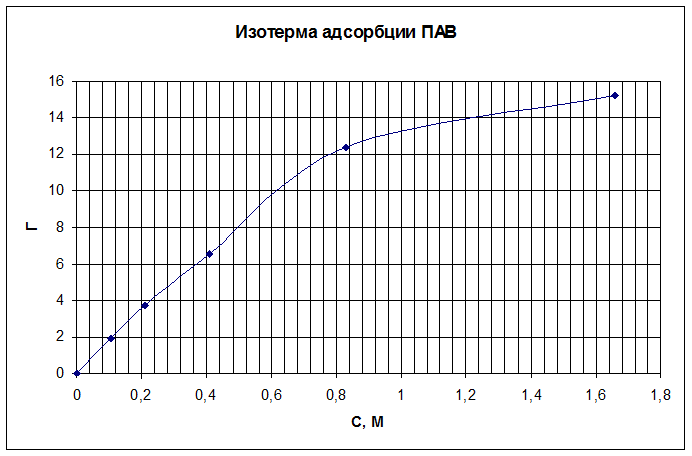
8. Строим изотерму адсорбции ПАВ в координатах Г=f(M):
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.