Определение скорости свободного падения шарообразных частиц. Параметры Лященко и их использование. Формулы для расчета конечных скоростей свободного падения

2.2 Свободное падение

2.2.1 Определение скорости свободного падения шарообразных частиц

Как уже говорилось выше, свободным называется падение одиночного тела в неограниченном пространстве или падение массы тел при небольшой объемной концентрации (l< 0,1).

Скорости свободного падения определяются: по теоретическим уравнениям; по эмпирическим и интерполяционным формулам; по графикам и по таблицам, составленным на основе экспериментальных данных.

Скорость свободного падения тела определяется взаимодействием следующих сил: гравитационной, подъемной (архимедовой), силами гидродинамического сопротивления (или аэродинамического).

При падении в неподвижной жидкости с начальной нулевой скоростью частица под действием силы тяжести будет постепенно увеличивать скорость падения, при этом, будет одновременно расти и сила сопротивления. По истечении некоторого промежутка времени частица приобретает практически постоянную скорость, называемую конечной скоростью падения. С этого момента сила тяжести и подъемная Архимедова сила уравновешиваются силой сопротивления

Для малых чисел Рейнольдса (Re<1, ламинарная область), скорость падения шаров может быть рассчитана исходя из того, что сила сопротивления выражается формулой:

R=, что соответствует зависимости

 - (16) в формуле общего сопротивления (14).

Сила тяжести G = V r g = mg, где V - объем тела, r - плотность тела, g - ускорение свободного падения, m - масса тела

Выталкивающая сила Архимеда А = V××g, где  - плотность среды в которую погружено тело.

С учетом того, что сила Архимеда направлена вверх, а сила тяжести вниз условие достижения телом конечной скорости свободного падения в области малых чисел Рейнольдса можно записать таким образом:

G - А =R_г/а; G – А =V r g - V  g = V () g = =()g; R_г/а=т.е. ()g =

отсюда получается формула Стокса (G.G. Stokes):

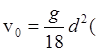
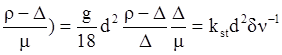, (17) где коэффициент Стокса, 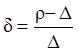 - так называемая относительная плотность.

Также можно вычислить конечную скорость свободного падения исходя из дифференциального уравнения движения частицы:

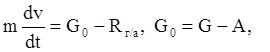(18), где -движущая сила, - ускорение частицы, m - масса частицы.

От начального момента движения скорость частицы постоянно растет, соответственно растет и силы сопротивления. В некоторый момент времени силы сопротивления становятся равными весу тела в среде. Ускорение же наоборот максимально в начальный момент времени движения частицы и постоянно уменьшается пока не станет равным нулю в от момент, когда силы сопротивления уравновесят вес тела в среде. Тогда:

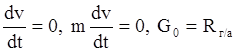
И далее вычисление идет по вышеизложенному.

Для частиц промежуточного размера (1< Re <1000) Алленом (A. Allen) экспериментально была установлена формула сопротивления:

R_г/а=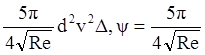 

т.к. 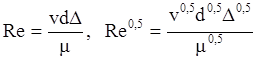 и по аналогии с вышеизложенным (при достижении конечной скорости свободного падения сила тяжести уравновешивается силами сопротивления), можно записать:

G - А =R или() g =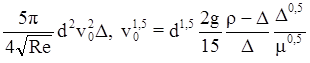 и соответственно

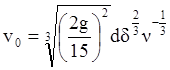, или

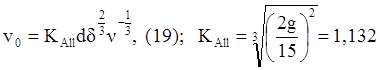- формула Аллена.

Реально формула Аллена «работает» достаточно надежно лишь при числах  30< Re <300. А достаточно хорошее приближение к экспериментальным данным для 0,1 < Re <5000 дает формула предложенная М.Я. Антонычевым и Ф.И. Нагирняком:

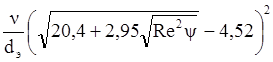 =  (20) - формула Антонычева-Нагирняка

Ошибка в определении скорости по этой формуле не превышает 9%.

При падении крупных частиц (Re >3000) коэффициент сопротивления приблизительно постоянная величина ( p/16). Тогда по аналогии с вышеизложенным получаем формулу Ньютона - Ритенгера (I. Newton, P.R. Rittinger):

G - А =R или () g = тогда

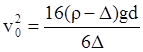 и

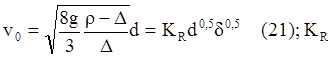- коэффициент Ритенгера.

Интерполяционные формулы для расчета скорости падения сферических частиц получены, как правило, на основании аппроксимации кривой Релея.

Наиболее простым способом аппроксимации является разделение кривой (см. рис. 2) на ряд участков, в каждом из которых зависимость между  и Re приближенно заменяется линейной. Поскольку кривая построена в логарифмических координатах, уравнение каждого ее участка имеет вид:

- некоторые постоянные для данного участка.

В этом случае скорость определяется по формуле, которую можно назвать обобщающей:

v₀=

Значения - известные величины для разных участков кривой Релея[1]. Полученные частные формулы скорости совпадают: при n=1 с формулой Стокса; для n=2/3 с формулой Аллена и n =1/2 с формулой Ньютона - Риттингера.

Обобщающую формулу, можно записать в более «читабельном» виде: