Измерение длины световой волны с помощью прозрачной дифракционной решётки. Многолучевая интерференция волн

Министерство образования РФ

Санкт – Петербургский государственный горный институт

(технический университет)

Кафедра общей и технической физики

ЛАБОРАТОРИЯ ОПТИКИ

РАБОТА 6

ИЗМЕРЕНИЕ ДЛИНЫ СВЕТОВОЙ ВОЛНЫ С ПОМОЩЬЮ

ПРОЗРАЧНОЙ ДИФРАКЦИОННОЙ РЕШЁТКИ.

Выполнил: студентка группы

Проверил:

САНКТ - ПЕТЕРБУРГ

2000

Введение. Дифракционная решётка – это прозрачная пластина с нанесёнными параллельными непрозрачными штрихами равной ширины b (рис. 1). Между штрихами

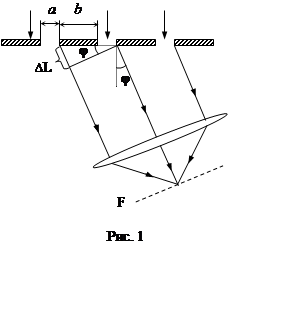возникают одинаковые прозрачные промежутки – прямоугольные  щели шириной a. Величина d = a + b называется постоянной (периодом) решётки.         

При прохождении света через щели происходит дифракция, в результате которой волны распространяются во всех направлениях. Идущие от всех щелей волны интерферируют (наблюдается т.н. многолучевая интерференция). Как результат, в различных направлениях (в зависимости от оптической разности хода ΔL) волны усиливают или ослабляют друг друга. Таким образом, дифракционная решётка осуществляет наложение двух процессов: дифракции на каждой отдельной щели и интерференции излучения от всех щелей.

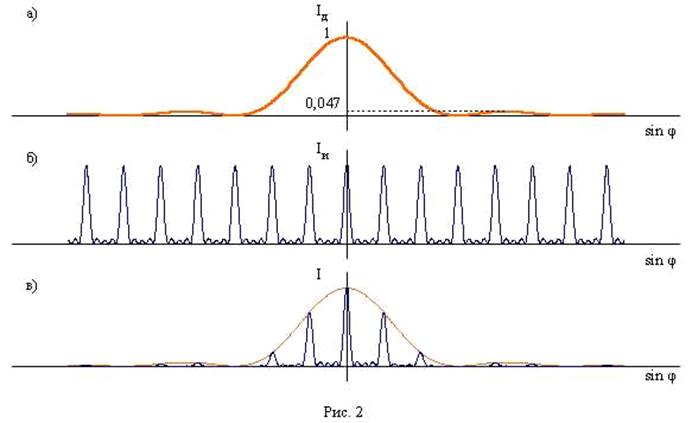
Дифракция на отдельной щели описывается зависимостью интенсивности от угла дифракции φ для прямоугольной щели шириной a(рис. 2, а):

                                                           I_д = I_0д(sin² u)/u² , uº πasinφ /λ  (1)

Многолучевая интерференция N волн , имеющих разность фаз δ, даёт зависимость:

I_и = I_0и (sin² N δ/2)/ (sin² δ/2) (2)

Разность фаз связана с оптической разностью хода: δ= 2π ΔL/λ. Разность хода для двух волн, идущих от двух соседних щелей под некоторым углом φ, можно выразить (рис. 1):

ΔL = dsinφ(3)

Тогда выражение (2) преобразуется к виду:

I_и = I_0и (sin² Nv)/ (sin² v), v º πdsin φ /λ                  (4)

Кривая I_и (sin φ) для случая пяти щелей и отношения  d/a = 3 (непрозрачный промежуток вдвое шире прозрачного) представлена на рис. 2, б.

В результате, дифракционная решётка даёт контур, описываемый функцией

(рис. 2, в):

                                            I= I_д I_и = I₀ (sin²u/ u²) (sin² Nv /sin² v),                                    (5)

uи v – см. (1) и (4).

Как видно, каждый интерференционный максимум порядка k = d/a (слева и справа от центрального) приходится на дифракционный минимум и пропадает. Интенсивны лишь те максимумы, которые заключены в пределах центрального дифракционного (интенсивности в максимумах, начиная с центрального, соотносятся как 1:0,047:0,017: …). Максимумы интерференции порядка, большего 2, оказываются вне пределов центрального дифракционного максимума и поэтому практически не видны. В отличие от одиночной щели, в данном случае максимумы оказываются узкими и достаточно далеко отстоящими друг от друга. При увеличении N (современные решётки имеют до 2000 штрихов на миллиметр) побочные максимумы многолучевой интерференции уменьшаются практически до нуля, и главные оказываются на чёрном фоне.

Рассмотрим условие главного максимума. Комбинируя выражение (3) для оптической разности хода с условием максимума интерференции: ΔL = ± kλ₀  (k =0, 1, 2, … - порядок интерференции), получаем:

d sin φ = ± kλ₀ (k =0, 1, 2, …)                                                (6)

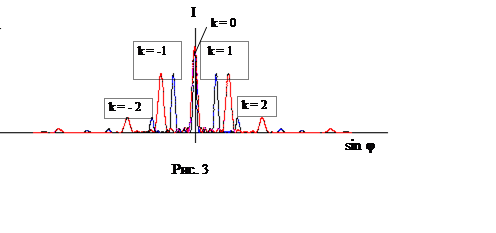
Последнее выражение носит название основного соотношения дифракционной решётки в случае нормального падения света. Оно даёт углы, под которыми наблюдаются максимумы для всех имеющихся в излучении длин волн в каждом порядке k; k - порядок спектра. Свойство дифракционной решётки, определяемое соотношением (6), - давать максимумы для разных длин волн под разными углами – лежит в основе спектроскопического применения этого устройства.

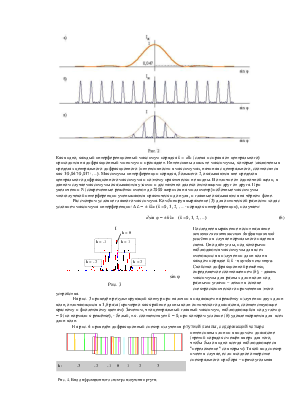
На рис. 3 приведён результирующий контур при наличии в падающем на решётку излучении двух длин волн, отличающихся в 1,6 раза (примерно как крайние длины волн оптического диапазона, соответствующие красному и фиолетовому цветам). Заметим, что центральный главный максимум, наблюдающийся под углом φ = 0 (по нормали к решётке), - белый, т.к. соответствует k = 0, при котором условие (6) удовлетворяется для  всех длин волн.

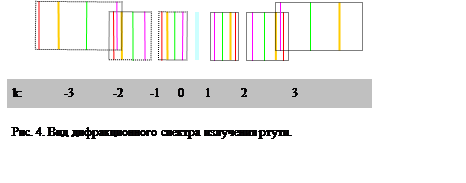
               На рис. 4 приведён дифракционный спектр излучения ртутной лампы, содержащий четыре интенсивных линии в видимом диапазоне (третий порядок смещён вверх для того, чтобы было видно всегда наблюдающееся "переложение" со вторым). Такой вид спектр имеет в случае, если входное отверстие спектрального прибора – прямоугольная щель (спектральная линия– это изображение входного отверстия в разных спектральных диапазонах).

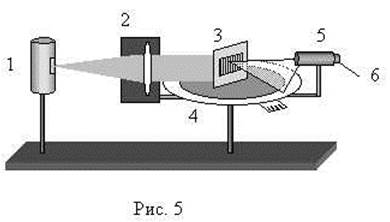Описание установки.  Источником оптического излучения с линейчатым спектром служит ртутная лампа 1 (рис. 5). Коллиматор 2 (собирающая линза, установленная на расстоянии, равном фокусному, от входной щели) формирует из расходящегося пучка параллельный, который падает на дифракционную решётку 3. Дифракционная решётка установлена на столике гониометра 4, так что её штрихи расположены вертикально, а плоскость перпендикулярна оси коллиматора. Продифрагировавшее на решётке излучение попадает в зрительную трубу