



Министерство образования РФ
Санкт-Петербургский государственный горный институт имени
Г.В. Плеханова (Технический Университет)

Расчётно-графическая работа № 2
Вариант №11
По дисциплине: Сопротивление материалов
Тема: Построение эпюр поперечных сил, изгибающих моментов и выбор сечения балок
Выполнил: студент группы ГМ-01-1 _________ / /
Проверил: доцент кафедры механики _________ / /
Санкт-Петербург
2003 г.
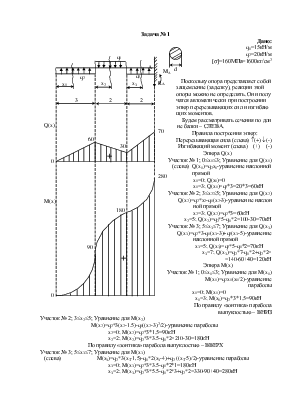
Дано:
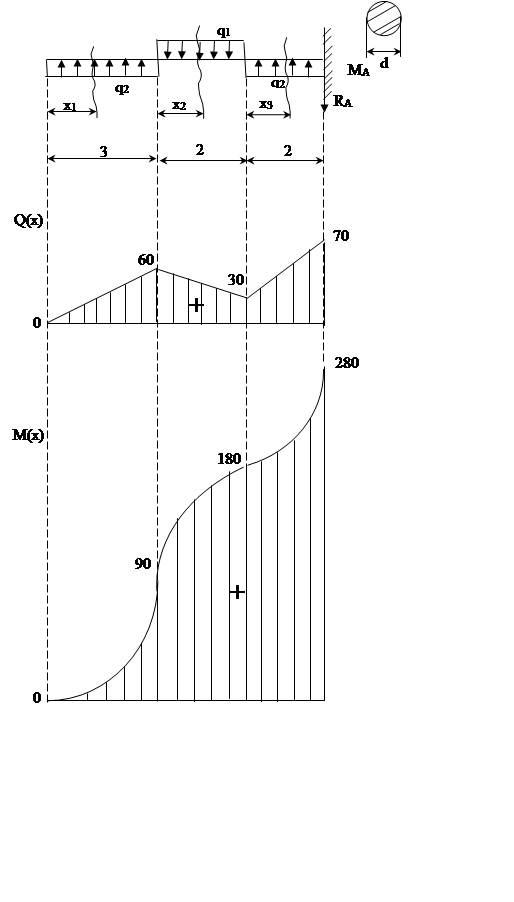 q1=15кН/м
q1=15кН/м
q2=20кН/м
[s]=160МПа=1600кг/см2
Поскольку опора представляет собой
защемление (заделку), реакции этой
опоры можно не определять. Они полу
чатся автоматически при построении
 эпюр
перерезывающих сил и изгибаю
эпюр
перерезывающих сил и изгибаю
щих моментов.
Правила построения эпюр:
Перерезывающая сила (слева) (+) ¯(-)
Изгибающий момент (слева) (+) (-)
Эпюра Q(x)
Участок № 1; 0£x1£3; Уравнение для Q(x1)
(слева) Q(x1)=q2x1-уравнение наклонной
прямой
x1=0; Q(x1)=0
x1=3; Q(x1)=q2*3=20*3=60кН
Участок № 2; 3£x2£5; Уравнение для Q(x2)
Q(x2)=q2*x2-q1(x2-3)-уравнение наклон
ной прямой
x2=3; Q(x2)=q2*3=60кН
x2=5; Q(x2)=q2*5-q1*2=100-30=70кН
Участок № 3; 5£x3£7; Уравнение для Q(x3)
Q(x3)=q2*3-q1(x3-3)+q2(x3-5)-уравнение
наклонной прямой
x3=5; Q(x3)=q2*5-q1*2=70кН
x3=7; Q(x3)=q2*7-q1*2+q2*2=
=140-60+40=120кН
Эпюра M(x)
Участок № 1; 0£x1£3; Уравнение для M(x1)
M(x1)=q2x1(x1/2)-уравнение
параболы
x1=0; M(x1)=0
x1=3; M(x1)=q2*3*1.5=90кН
выпуклостью – ВНИЗ
Участок № 2; 3£x2£5; Уравнение для M(x2)
M(x2)=q2*3(x2-1.5)-q1((x2-3)2/2)-уравнение параболы
x2=0; M(x2)=q2*3*1.5=90кН
x2=2; M(x2)=q2*3*3.5-q1*2=210-30=180кН
Участок № 3; 5£x3£7; Уравнение для M(x3)
(слева) M(x3)=q2*3(x3-1,5)-q1*2(x3-4)+q2 ((x3-5)/2)-уравнение параболы
x3=0; M(x3)=q2*3*3.5-q1*2*1=180кН
x3=2; M(x3)=q2*3*5.5-q1*2*3+q2*2=330-90+40=280кН
Реакция в заделке:
åY=0; q2*3-q1*2+q2-Rc=0;
60-30+40-Rc=0; Rc=70кН
Момент в заделке:
åMA=0; -q2*3*5.5+q1*2*3-q2*2*1+MA=0;
-330+90-40+MA=0; MA=280кН*м
Условие прочности:
smax = |Mизгmax| / W £ [s]
Момент сопротивления для круглого сечения: W = (pd3) / 32=280*103 /160*106=1,75*10-3м
Из условия прочности:
d = 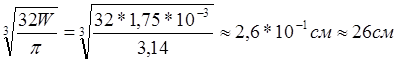
|
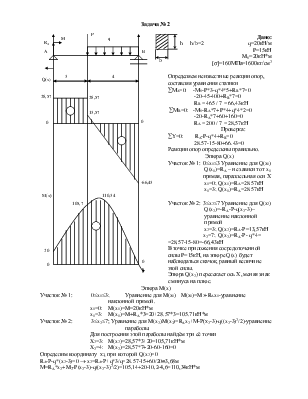
q=20кН/м
P=15кН
|
[s]=160МПа=1600кг/см2
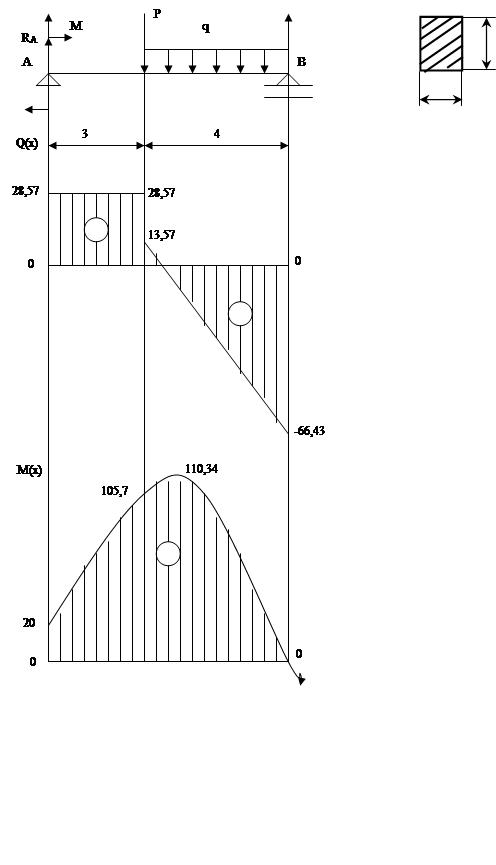
Определяем неизвестные реакции опор, составляя уравнения статики
åМА=0: -М0-P*3-q*4*5+RB*7=0
-20-45-400+RB*7=0
RB = 465 / 7 = 66,43кН
åМB=0: -М0-RA*7+P*4+q*4*2=0
-20-RA*7+60+160=0
RA = 200 / 7 = 28,57кН
Проверка:
åY=0: RA-P-q*4+RB=0
28.57-15-80+66.43=0
Реакции опор определены правильно.
Эпюра Q(x)
Участок № 1: 0£x1£3 Уравнение для Q(x1)
Q(x1)=RA – не зависит от x1
прямая, параллельная оси Х
x1=0; Q(x1)=RA=28.57кН
x1=3; Q(x1)=RA=28.57кН
Участок № 2: 3£x2£7 Уравнение для Q(x2)
Q(x2)=-RА-Р-q(x2-3)–уравнение наклонной прямой
x2=3; Q(x2)=RА-Р=13,57кН
x2=7; Q(x2)=RА-Р- q*4= =28,57-15-80=-66,43кН
В точке приложения сосредоточенной силы P=15кН, на эпюре Q(x) будет наблюдаться скачок, равный величине этой силы.
Эпюра Q(x2) пересекает ось Х, меняя знак с минуса на плюс.
Эпюра M(x)
Участок № 1: 0£x1£3; Уравнение для M(x1) M(x1)=M2+RAx1-уравнение
наклонной прямой.
x1=0: M(x1)=M=20кН*м
x1=3: M(x1)=M+RA*3=20+28.57*3=105.71кН*м
Участок № 2: 3£x2£7; Уравнение для M(x2)M(x2)=RАx2+М-Р(х2-3)-q((x2-3)2/2)-уравнение параболы.
Для построения этой параболы найдём три её точки
X2=3: M(x2)=28,57*3+20=105,71кН*м
X2=4: M(x2)=28,57*7+20-60-160=0
Определим координату х2, при которой Q(x2)=0
RА-Р-q*(x2-3)=0 ® x2=RА-Р+q*3/q=28.57-15+60/20@3,68м
М=RA*x2+M2-P(x2-3)-q((x2-3)2/2)=105,14+20-10,2-4,6=110,34кН*м
Условие прочности:
smax = |Mизгmax| / W £ [s]
Максимальный
изгибающий момент с эпюры M(x):![]()
W=|Mизгmax|/[sИ]=110,34*103/160*106=0,69*10-3
Момент сопротивления для прямоугольного сечения: W = (bh2) / 6; h/b=2 h=2b;
Из условия прочности:
W = (4b3) /6 ;
b ³ 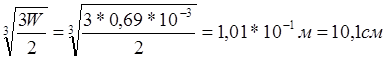
h = 2b = 10.1*2 = 20.2см
|
 |
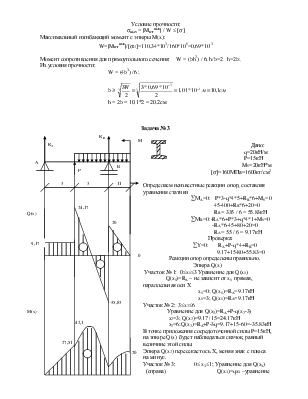
q=20кН/м
P=15кН
M0=20кН*м
[s]=160МПа=1600кг/см2
Определяем неизвестные реакции опор, составляя уравнения статики
åМA=0: P*3-q*4*5+RB*6+M0=0
![]() 45-400+RB*6+20=0
45-400+RB*6+20=0
![]() RB = 335 / 6 = 55.83кН
RB = 335 / 6 = 55.83кН
![]() åМB=0:-RA*6+P*3+q*4*1+M0=0
åМB=0:-RA*6+P*3+q*4*1+M0=0
-RA*6-45+80+20=0
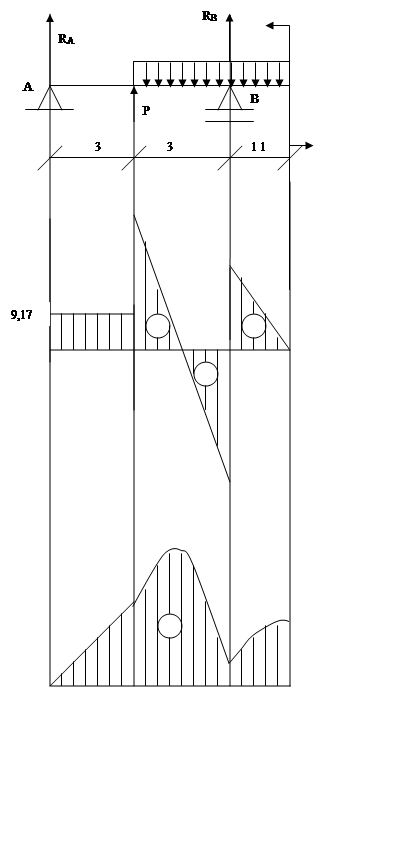
RA = 55 / 6 = 9.17кН
Проверка:
åY=0: RA+P-q*4+RB=0
![]() 9.17+15-80+55.83=0
9.17+15-80+55.83=0
Реакции опор определены правильно.
Эпюра Q(x)
Участок № 1: 0£x1£3 Уравнение для Q(x1)
Q(x1)=RA – не зависит от x1 прямая, параллельная оси Х
x1=0; Q(x1)=RA=9.17кН
![]() x1=3;
Q(x1)=RA=9.17кН
x1=3;
Q(x1)=RA=9.17кН
![]() Участок
№ 2: 3£x2£6
Участок
№ 2: 3£x2£6
Уравнение для Q(x2)=RA+P-q(x2-3)
|
x2=6;Q(x2)=RA+P-3q=9.17+15-60=-35.83кН
![]()
|
|
Участок № 3: 0£ x3£1; Уравнение для Q(x3)
(справа) Q(x3)=qx3 –уравнение наклонной прямой
x3=0; Q(x3)=0
x3=1;Q(x3)=q*1=20кН
В точке приложения реакции опоры RB=55,83кН, на эпюре Q(x) будет наблюдаться скачок, равный величине этой силы.
Эпюра M(x)
Участок № 1: 0£x1£3; Уравнение для M(x1) M(x1)=RAx1-уравнение наклонной прямой.
x1=0: M(x1)=0
x1=3: M(x1)=RA*3=9,17*3=27,51кН*м
Участок № 2: 3£x2£6; Уравнение для M(x2) M(x2)=RAx2+P(x2-3)-q((x2-3)2/2)-уравнение параболы.
X2=3: M(x2)=9.17*3+0-0=27.51кН*м
X2=6: M(x2)=RA*6+P*3-q*3*1.5=9.17*6+15*3-20*4,5=10кН*м
Участок № 3: 0£ x3£1; Уравнение для M(x3)
(справа) M(x3)=M-q(x32/2) –уравнение параболы.
x3=0; M(x3)=M=20кН*м
x3=1;M(x3)=M-q*0.5=20-10=10кН*м
Эпюра Q(x2) пересекает ось Х, меняя знак с плюса на минус.
Определим координату х2, при которой Q(x2)=0
Q(x2)=RA+P-q*(x2-3)=0 ® x2=RA+P+q*3/q=(9.17+15+60)/20=4,2м
M11=RA*x2+P(x2-3)-q((x2-3)2/2=38,5+18-14,4=42,1кН*м
Условие прочности:
smax = |Mизгmax| / W £ [s]
Из условия прочности:
W =42,1*103/160*106=0,26*10-3м3=260см3
Из таблицы стандартных профилей ГОСТ-8239-56 находим ближайшее большее к расчётному значение W = 289см3.
Выбираем двутавр № 24.
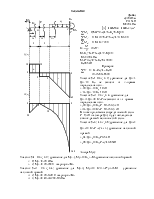
Задача№4
Дано:
![]()
![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
 P=15kH
P=15kH
M=20 kHм
|
![]() =0;М-Р*2-q*4*6+Rс*8-Mс=0
=0;М-Р*2-q*4*6+Rс*8-Mс=0
![]() M- 10*8+P*6+q*4*2- MC=0
M- 10*8+P*6+q*4*2- MC=0
![]() ; M- RA*2=0
; M- RA*2=0
RA=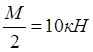 ;
;
M-RA*8+P*6+q*4*2-MC=0 :
MC=190 kHм
М-Р*2-q*4*6+Rс*8-190=0:
Rс=85 kH
Проверка:
![]() ; RA-Р-q*4+ Rс=0
; RA-Р-q*4+ Rс=0
10-15-80+85=0
Участок №1 ![]() ; уравнение для Q(x1), Q(x1)= Rа-
не зависит от x1-прямая
параллельна оси x.
; уравнение для Q(x1), Q(x1)= Rа-
не зависит от x1-прямая
параллельна оси x.
x1=0; Q(x1)= Rа=10 кН
x1=3; Q(x1)= Rа=10 кН
|
x2=0; Q(x2)= RА-Р =10-15=-5 кН
x2=3; Q(x2)= RА-Р =10-15=-5 кН
В точке приложения сосредоточенной силы Р=15 кН на эпюре Q(x) будет наблюдаться скачок, равный величине этой силы.
Участок №3; ![]() ;уравнение для Q(x3): Q(x3)= RА-Р -q*(x3–4) уравнение наклонной прямой
;уравнение для Q(x3): Q(x3)= RА-Р -q*(x3–4) уравнение наклонной прямой
x3=4; Q(x3)= RА-Р=-5 kH
x3=8; Q(x3)= RА-Р- q*4=-85kH
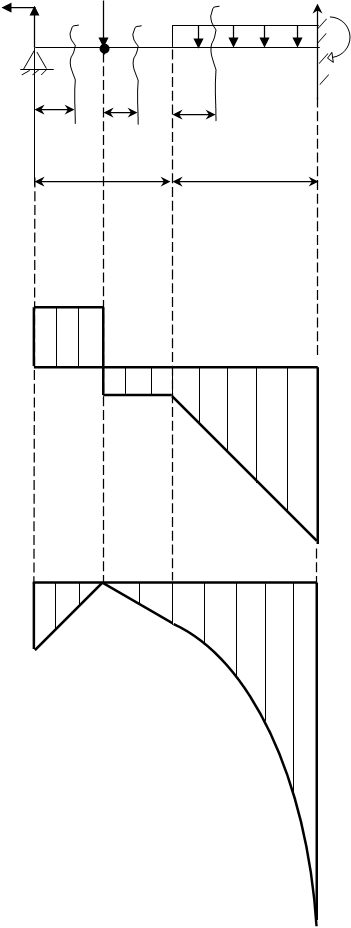
Эпюра М(х):
Участок №1 ![]() ; уравнение для М(x1), М(x1)= RАx1-M -уравнение наклонной прямой
; уравнение для М(x1), М(x1)= RАx1-M -уравнение наклонной прямой
x1=0; М(x1)=-20 kHм
x1=2; М(x1)= 20-20=0 – шарнир в «В»
Участок №2: ![]() ; уравнение для М(x2), М(x2)= RА*x2-Р*(x2-2)-M – уравнение
; уравнение для М(x2), М(x2)= RА*x2-Р*(x2-2)-M – уравнение
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.