|
№ |
Поддиапазон изменения, хi |
Частота, ni |
Вероятность Рi |
Накопленная вероятность SРi |
|
1 |
48,2-42,62 |
2 |
0,04 |
0,04 |
|
2 |
42,62-37,04 |
3 |
0,06 |
0,10 |
|
3 |
37,04-31,46 |
3 |
0,06 |
0,16 |
|
4 |
31,46-25,88 |
11 |
0,22 |
0,38 |
|
5 |
25,88-20,3 |
11 |
0,22 |
0,60 |
|
6 |
20,3-14,72 |
14 |
0,28 |
0,88 |
|
14,72-9,1 |
6 |
0,12 |
1,00 |
Строим гистограммы распределения случайной величины х (по частным и накопленным частотам).
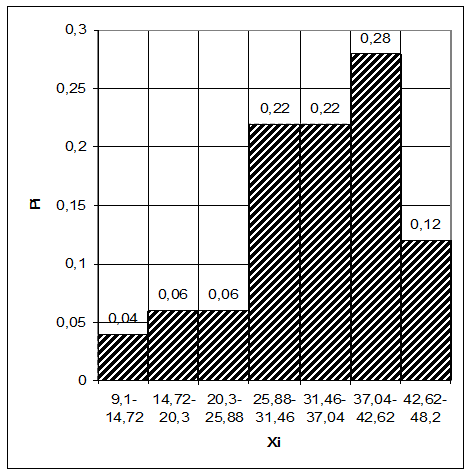
Рис.1. Гистограмма распределения xi от Pi
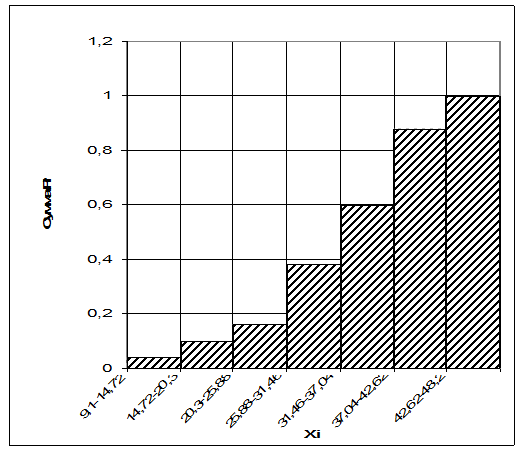
Рис.2. Гистограмма распределения xi от SPi
Для y делаем аналогичные расчеты:
ymin = 26,76, ymax = 71,04.
D = ymax – ymin = 71,04 – 26,76 = 44,28.
m = 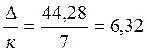 – шаг
поддиапазона.
– шаг
поддиапазона.
к – число поддиапазонов, равное 7.
Находим частоту попадания случайных величин в каждый из интервалов и составляем вспомогательную табл.3, для построения гистограмм.
|
№ |
Поддиапазон изменения, yi |
Частота, ni |
Накопленная частота, Sni |
Вероятность Рi |
Накопленная вероятность SРi |
|
1 |
71,04-64,72 |
7 |
3 |
0,06 |
0,06 |
|
2 |
64,72-58,4 |
13 |
24 |
0,42 |
0,48 |
|
3 |
58,4-52,08 |
6 |
41 |
0,34 |
0,82 |
|
4 |
52,08-45,76 |
9 |
44 |
0,06 |
0,88 |
|
5 |
45,76-39,44 |
7 |
50 |
0,12 |
1,00 |
|
6 |
39,44-33,12 |
5 |
|||
|
7 |
33,12-26,76 |
3 |
Строим гистограммы распределения случайной величины y (по частным и накопленным частотам).
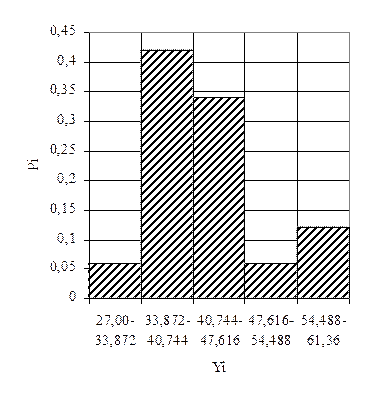
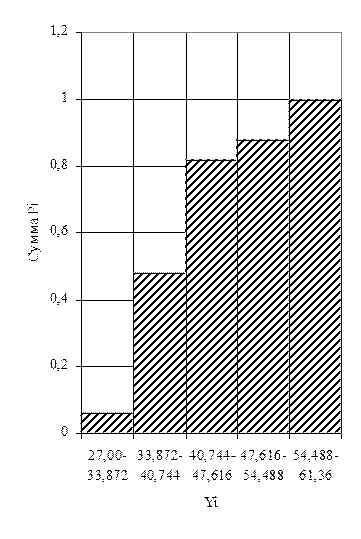
Рис.3. Гистограмма распределения yi от Pi. Рис.4. Гистограмма распределения yi от SPi
II. Получение начальных и центральных моментов выборочного
распределения
Начальные моменты выборочного распределения рассчитываются по формуле:
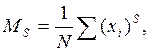 где
где
MS – начальный момент s-гo порядка; xi – i-ое значение случайной величины, i=1, 2, ... N.
Центральные моменты рассчитываются по формуле:
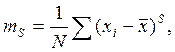 где
где
тS – центральный момент s-гo
порядка; ![]() – среднее
арифметическое,
– среднее
арифметическое, 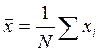 (на-чальный
момент первого порядка).
(на-чальный
момент первого порядка).
Наиболее часто в практике используется центральный момент второго порядка (оценка дисперсии):
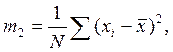
а
также ![]() (среднее квадратичное
отклонение).
(среднее квадратичное
отклонение).
Для оценки формы кривой распределения используются центральные моменты третьего и четвёртого порядков, которые вычисляются по формулам:
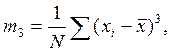
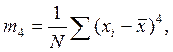
Таблица 4
Значения начальных и центральных моментов
|
М1 |
М2 |
М3 |
М4 |
m1 |
m2 |
m3 |
m4 |
|
52,85 |
2852,048 |
156872,2 |
8776514,315 |
-21,3808 |
609,2889 |
-18724,4 |
605099,2 |
Для оценки степени асимметрии распределения используется коэффициент асимметрии:
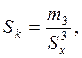
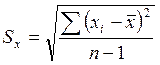 .
.
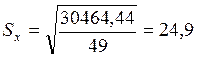 ;
; 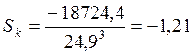 .
.
а для оценки характеристики степени «крутости» – показатель эксцесса:
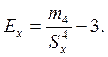
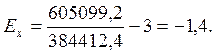
Для оценки близости распределения к нормальному рассчитываются вспомогательные коэффициенты:
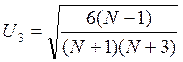 и
и 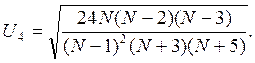
Если ![]() ,
a
,
a ![]() то закон
распределения можно считать нормальным.
то закон
распределения можно считать нормальным.
По расчету получаем следующее:
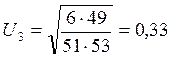 ;
; 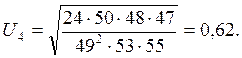
-1,21 < 0,66,
-1,4 < 1,24.
Вывод:
т.к. условия ![]() , a
, a ![]() соблюдаются, то можно сделать вывод о том, закон распределения можно
считать нормальным.
соблюдаются, то можно сделать вывод о том, закон распределения можно
считать нормальным.
III. Получение коэффициента корреляции
Вычисление коэффициента корреляции удобно производить по следующей формуле:
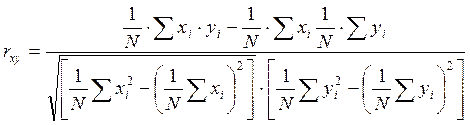
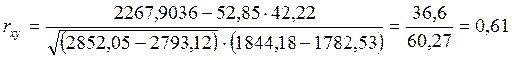
IV. Нахождение теоретической линии регрессии
Для нахождения по методу наименьших квадратов коэффициентов линейного уравнения Y=a+bxможно воспользоваться следующими формулами:
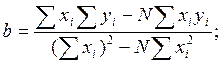
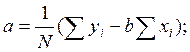
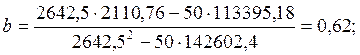
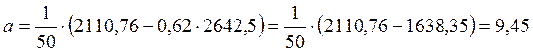 ;
;
остаточная дисперсия:
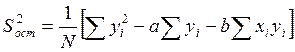 ;
;
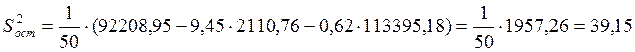 .
.
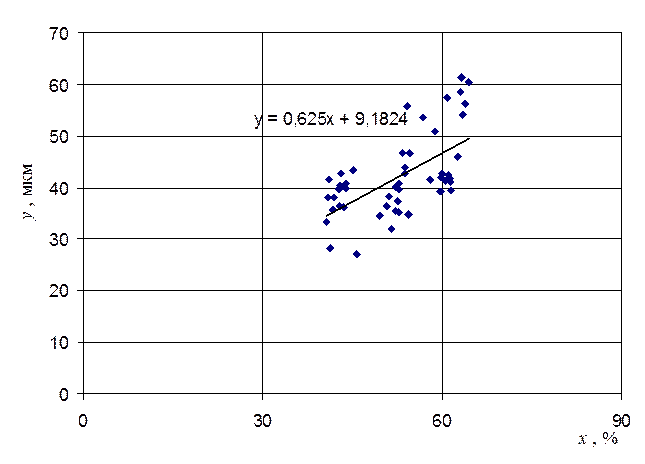
Рис.5. Линия регрессии
Вывод: При х2 (% твердого на выходе мельницы) и y2(+100 мкм на выходе мельницы) мы наблюдаем прямо пропорциональную зависимость между х и у, т.е. при увеличении x значение у увеличивается.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.