Определение размеров частиц дисперсных систем турбидиметрическим методом. Константы, не зависящие от длины волны

Федеральное агентство по образованию Российской Федерации

Государственное образовательное учреждение высшего профессионального образования

Санкт-Петербургский  Государственный  Горный институт им. Г.В.Плеханова

(технический университет)

КАФЕДРА ОБЩЕЙ И ФИЗИЧЕСКОЙ ХИМИИ

Отчёт по лабораторной работе № 4.

По дисциплине:                                    Физическая химия                                                        л

(наименование учебной дисциплины согласно учебному плану)

Тема:   «Определение размеров частиц дисперсных систем турбидиметрическим методом»

Выполнил:    студент        гр. ОП-04         ______________                       / /

                                                                                                                      ^{(подпись)                                                        (Ф.И.О.)}

ОЦЕНКА: _____________

Дата: __________________

ПРОВЕРИЛ:

Руководитель:      доцент                ______________                     / /

                                            ^{(должность)                                   (подпись)                                                          (Ф.И.О.)}

Санкт-Петербург

2006 г.

Цель работы:

Экспериментальное определение размеров частиц высокодисперсных систем.

Сущность работы:

Уравнение Рэлея может быть использовано для определения размеров частиц формы, близкой к сферической, если их радиус R не превышает 0,1l длины волны падающего света. Уравнение Рэлея определяет интенсивность рассеянного света от размера частиц, угла рассеяния и длины волны падающего света:

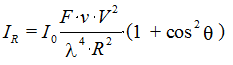                                                            (1)

где I₀ – интенсивность падающего света, I_R – интенсивность рассеянного света, F – функция показателей преломления дисперсной и дисперсионной среды, равная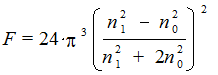                                             

где n₁, n₀ – показатели преломления дисперсной и дисперсионных фаз соответственно, n - концентрация частиц в единице объема, V – объем частицы, l - длина волны падающего света, R – расстояние частицы от источника света (оптический путь), Q - угол рассеяния.

Из уравнения Рэлея радиус частицы равен:

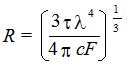                                                                                (2)

где с – концентрация взвешенных частиц, t - мутность системы, определяемая из уравнения (1), как I_s/I₀.

Необходимым условием использования уравнений (1) и (2) для дисперсных систем является отсутствие поглощения света, а также минимум вторичного светорассеяния. Поэтому уравнение Рэлея применимо только для «белых» золей, т.е., не поглощающих свет дисперсных систем при очень низких концентрациях дисперсной фазы.

Для дисперсных сред, неудовлетворяющих уравнению Рэлея используют турбидиметрические измерения. Турбидиметрические методы основаны на измерении интенсивности проходящего через дисперсную среду света. Рассеянный свет можно считать фиктивно поглощенным, и поэтому для проходящего света можно принять закон Бугера – Ламберта – Бера для определения кажущейся оптической плотности. Для дисперсных сред закон Бугера –Ламберта – Бера связывает мутность среды с кажущейся оптической плотности:

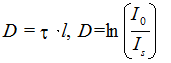                                                                        (3)

Мутность t = I_s/I0 , а отсюда и оптическая плотность D в соответствии с уравнениями (1) и (2) пропорциональна концентрации и квадрату объема частиц. Это позволяет определять размеры частиц и их концентрацию по кажущейся оптической плотности системы с помощью турбидиметрических измерений.

При увеличении размеров частиц закон Рэлея не выполняется, и интенсивность рассеянного света становится обратно пропорциональной длине волны в степени меньше чем четвертая. В общем случае для поглощающих золей степень при длине волны становится дробной, что делает невозможным использование уравнения Рэлея.  Если размер (диаметр) взвешенных частиц составляет от 1/10 до 1/3 длины световой волны и показатели преломления частиц и среды не сильно различаются, то в случае турбидиметрических измерений можно пользоваться эмпирическим уравнением Геллера:

D = kλ^-n и τ=k^’ λ^-n                                                                 (4)

где k и k’ – константы, не зависящие от длины волны.

Зависимость lgD от lg( в соответствии с уравнением (4) представляет собой прямую, тангенс угла наклона которой равен показателю степени n с минусом. Показатель степени связан с длиной волны и размером частиц эмпирическим соотношением:

Z=8πr/λ                                                                                             (5)

которое табулировано для n < 4 (табл. 1). С увеличением Z значение n уменьшается в пределе к 2 для частиц, радиус которых больше длины волны. При малых значениях Z показатель степени n стремится к 4 и выполняется уравнение Рэлея.

Таблица 1. Показатель степени n в уравнении Геллера в зависимости от параметра Z

n	Z	n	Z
3,812	2,0	2,807	5,5
3,686	2,5	2,657	6,0
3,573	3,0	2,533	6,5
3,436	3,5	2,457	7,0
3,284	4,0	2,379	7,5
3,121	4,5	2,329	8,0
3,060	5,0

Порядок выполнения работы:

Приготовлены два раствора:

Раствор (I): 1,1 г Na₂SO₄×10H₂O растворен в 50 мл глицерина

Раствор (2): 2,45 г BaSO₄×2H₂O растворен в 50 мл глицерина

- приготовить золь BaSO₄: приготовить заданный раствор (а или б или с), полученный из раствора (I) , осторожно прилить к раствору, полученному разбавлением раствора (II), после чего растворы перемешать. В зависимости от соотношения спирта и воды при разбавлении получают золи с разной величиной частиц.

а)1 см³ раствора (I) + 5 см³ воды + 4 см³ спирта

1 см³ раствора (II) + 5 см³ воды + 4 см³ спирта

б) 1 см³ раствора (I) + 2 см³ воды + 3 см³ спирта

1 см³ раствора (II) + 2 см³ воды + 3 см³ спирта

с)1 см³ раствора (I) + 1,5 см³ воды + 3,5 см³ спирта

1 см³ раствора (II) + 1,5 см³ воды + 3,5 см³ спирта

- залить исследуемый золь в кювету с толщиной 1 см, залить воду