





















Министерство общего и профессионального образования
Российской Федерации
Санкт-Петербургский государственный горный институт им. Г.В. Плеханова
(технический университет)
КУРСОВАЯ РАБОТА
|
По дисциплине __________________________________________________________
________________________________________________________________________
(наименование учебной дисциплины согласно учебному плану)
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
|
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
|
|||
|
|||
Автор: студент гр. _______ ____________________ /_______________/
(подпись) (Ф.И.О.)
ОЦЕНКА: ____________
Дата: ___________________
ПРОВЕРИЛ
|
|
(должность) (подпись) (Ф.И.О.)
Санкт-Петербург
2001 год
|
Министерство общего и профессионального образования Российской Федерации |
|||
|
Санкт-Петербургский государственный горный институт им Г.В. Плеханова (технический университет) |
|||
|
УТВЕРЖДАЮ Заведующий кафедрой ___________ /________/ "___"__________200_ г. |
|||
|
Кафедра __________________________________
КУРСОВОЙ ПРОЕКТ / РАБОТА
|
По дисциплине _________________________________________________________
_______________________________________________________________________
(наименование учебной дисциплины согласно учебному плану)
ЗАДАНИЕ
|
|
|
1. Тема проекта __________________________________________________________
________________________________________________________________________________________________________________________________________________
|
2. Исходные данные к проекту ______________________________________________
|
xi |
yi |
xi |
yi |
xi |
yi |
xi |
yi |
xi |
yi |
|
0,09 |
2,54 |
2,85 |
22,47 |
4,44 |
156,87 |
5,91 |
456,78 |
8,54 |
867,67 |
|
0,15 |
2,76 |
3,08 |
25,41 |
4,76 |
197,98 |
6,98 |
600,98 |
8,86 |
900,54 |
|
0,87 |
2,98 |
3,56 |
54,89 |
5,05 |
242,65 |
7,12 |
645,65 |
9,08 |
956,87 |
|
1,58 |
6,45 |
3,92 |
80,87 |
5,45 |
345,87 |
7,65 |
789,09 |
9,45 |
977,08 |
|
2,75 |
20,65 |
4,07 |
85,75 |
5,72 |
400,89 |
8,13 |
800,98 |
9,55 |
999,54 |
3. Срок сдачи законченного проекта _________________________________________
|
|
||||
Руководитель проекта _________ ________________ /_______________/
(должность) (подпись) (Ф.И.О.)
Дата выдачи задания: ____________________
Данная курсовая работа содержит пример решения задачи “Аппроксимация квадратичной функции методом наименьших квадратов”. Работа выполнена в офисных приложениях Microsoft Word и Microsoft Excel, также представлен текст программы в интегрированной среде программирования Pascal. Содержит: страниц 25,таблиц 9, блок-схема 1, графиков 3.
The summary
Given term paper is kept an example of solution of the problem “Approcsimation function method least square”. Functioning is executed in office exhibits Microsoft Word and Microsoft Excel, also presented text of program in Pascal programming integrated environment. This term paper consist of 25 pages, 9 tables, 1 block-scheme, 3 graphics.
Аннотация. 3
Оглавление. 4
Введение. 5
Задание. 6
Расчетные формулы. 6
Приложение №1. Программа с необходимыми комментариями. 15
Приложение №2. Результаты счета. 17
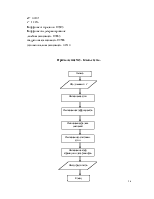
Приложение№3. Блок-схема. 19
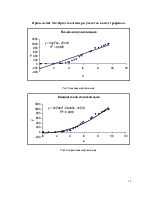
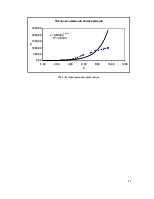
Приложение №4.Представление результатов в виде графиков. 19
Приложение №5. Отображение в режиме формул в Microsoft Excel. 21
Вывод. 24
Библиографический список. 25
Целью выполнения курсовой работы является развитие и закрепление навыков работы с табличным процессом Microsoft Excel, изучаемый в курсе информатики и применение их для самостоятельного решения с помощью компьютера задач из предметной области, связанной с исследованиями, а также закрепление навыков программирования на языке Pascal.
1) Используя метод наименьших
квадратов функцию ![]() , заданную таблично,
аппроксимировать
, заданную таблично,
аппроксимировать
a)
Многочленом
первой степени ![]() ;
;
b)
![]() Многочленом второй степени;
Многочленом второй степени;
c)
Экспоненциальной
зависимостью ![]() .
.
2) Для каждой зависимости вычислить коэффициент детерминированности.
3) Вычислить коэффициент корреляции (только в случае a).
4) Для каждой зависимости построить линию тренда.
5) Используя функцию ЛИНЕЙН вычислить числовые характеристики зависимости y от x.
6) Сравнить свои вычисления с результатами, полученными при помощи функции ЛИНЕЙН.
7) Сделать вывод, какая из
полученных формул наилучшим образом аппроксимирует функцию ![]() .
.
8) Написать программу на одном из языков программирования и сравнить результаты счёта с полученными выше.
Таблица 1.
|
xi |
yi |
xi |
yi |
xi |
Yi |
xi |
yi |
xi |
yi |
|
0,09 |
2,54 |
2,85 |
22,47 |
4,44 |
156,87 |
5,91 |
456,78 |
8,54 |
867,67 |
|
0,15 |
2,76 |
3,08 |
25,41 |
4,76 |
197,98 |
6,98 |
600,98 |
8,86 |
900,54 |
|
0,87 |
2,98 |
3,56 |
54,89 |
5,05 |
242,65 |
7,12 |
645,65 |
9,08 |
956,87 |
|
1,58 |
6,45 |
3,92 |
80,87 |
5,45 |
345,87 |
7,65 |
789,09 |
9,45 |
977,08 |
|
2,75 |
20,65 |
4,07 |
85,75 |
5,72 |
400,89 |
8,13 |
800,98 |
9,55 |
999,54 |
Эмпирическая формула:
![]() . (1)
. (1)
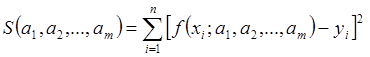 (2)
(2)
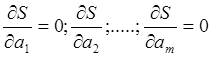 (3)
(3)
В случае линейной зависимости ![]() система примет вид:
система примет вид:
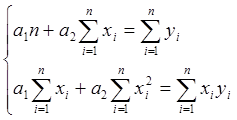 (4)
(4)
Эта линейная система может быть решена любым известным методом (методом Гаусса, простых итераций, формулами Крамера).
В случае квадратичной зависимости ![]() система примет вид:
система примет вид:
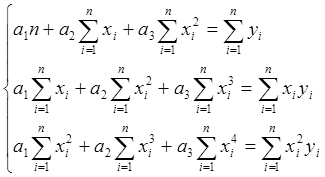 (5)
(5)
Экспоненциальная зависимость:
![]() (6)
(6)
где ![]() и
и ![]() неопределённые коэффициенты.
неопределённые коэффициенты.
Линеаризация достигается путём логарифмирования равенства (6), после чего получаем соотношение:
![]() (7)
(7)
![]()
Коэффициент корреляции вычисляется по формуле:
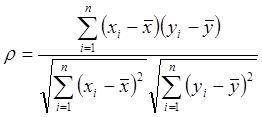 (8)
(8)
Корреляционное отношение вычисляется по формуле:
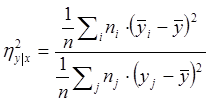 (9)
(9)
Коэффициент детерминированности определяется по формуле:
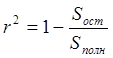 (10)
(10)
Таблицы выполненные средствами Microsoft Excel с пояснениями.
Для проведения расчётов данные целесообразно расположить в виде таблицы 2, используя средства табличного процессора Microsoft Excel.
Таблица 2.
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
||||||||||||
|
1 |
0,09 |
2,54 |
0,01 |
0,23 |
0,00 |
0,00 |
0,02 |
0,93 |
0,08 |
|||||||||||
|
2 |
0,15 |
2,76 |
0,02 |
0,41 |
0,00 |
0,00 |
0,06 |
1,02 |
0,15 |
|||||||||||
|
3 |
0,87 |
2,98 |
0,76 |
2,59 |
0,66 |
0,57 |
2,26 |
1,09 |
0,95 |
|||||||||||
|
4 |
1,85 |
6,45 |
3,42 |
11,93 |
6,33 |
11,71 |
22,08 |
1,86 |
3,45 |
|||||||||||
|
5 |
2,75 |
20,65 |
7,56 |
56,79 |
20,80 |
57,19 |
156,17 |
3,03 |
8,33 |
|||||||||||
|
6 |
2,85 |
22,47 |
8,12 |
64,04 |
23,15 |
65,98 |
182,51 |
3,11 |
8,87 |
|||||||||||
|
7 |
3,08 |
25,41 |
9,49 |
78,26 |
29,22 |
89,99 |
241,05 |
3,24 |
9,96 |
|||||||||||
|
8 |
3,56 |
54,89 |
12,67 |
195,41 |
45,12 |
160,62 |
695,65 |
4,01 |
14,26 |
|||||||||||
|
9 |
3,92 |
80,87 |
15,37 |
317,01 |
60,24 |
236,13 |
1242,68 |
4,39 |
17,22 |
|||||||||||
|
10 |
4,07 |
85,75 |
16,56 |
349,00 |
67,42 |
274,40 |
1420,44 |
4,45 |
18,12 |
|||||||||||
|
11 |
4,44 |
156,87 |
19,71 |
696,50 |
87,53 |
388,63 |
3092,47 |
5,06 |
22,45 |
|||||||||||
|
12 |
4,76 |
197,98 |
22,66 |
942,38 |
107,85 |
513,37 |
4485,75 |
5,29 |
25,17 |
|||||||||||
|
13 |
5,05 |
242,65 |
25,50 |
1225,38 |
128,79 |
650,38 |
6188,18 |
5,49 |
27,73 |
|||||||||||
|
14 |
5,45 |
345,87 |
29,70 |
1884,99 |
161,88 |
882,24 |
10273,20 |
5,85 |
31,86 |
|||||||||||
|
15 |
5,72 |
400,89 |
32,72 |
2293,09 |
187,15 |
1070,49 |
13116,48 |
5,99 |
34,28 |
|||||||||||
|
16 |
5,91 |
456,78 |
34,93 |
2699,57 |
206,43 |
1219,97 |
15954,46 |
6,12 |
36,19 |
|||||||||||
|
17 |
6,98 |
600,98 |
48,72 |
4194,84 |
340,07 |
2373,68 |
29279,99 |
6,40 |
44,66 |
|||||||||||
|
18 |
7,12 |
645,65 |
50,69 |
4597,03 |
360,94 |
2569,92 |
32730,84 |
6,47 |
46,07 |
|||||||||||
|
19 |
7,65 |
789,09 |
58,52 |
6036,54 |
447,70 |
3424,88 |
46179,52 |
6,67 |
51,03 |
|||||||||||
|
20 |
8,13 |
800,98 |
66,10 |
6511,97 |
537,37 |
4368,80 |
52942,29 |
6,69 |
54,36 |
|||||||||||
|
21 |
8,54 |
867,67 |
72,93 |
7409,90 |
622,84 |
5319,02 |
63280,56 |
6,77 |
57,78 |
|||||||||||
|
22 |
8,86 |
900,54 |
78,50 |
7978,78 |
695,51 |
6162,19 |
70692,03 |
6,80 |
60,27 |
|||||||||||
|
23 |
9,08 |
956,87 |
82,45 |
8688,38 |
748,61 |
6797,41 |
78890,49 |
6,86 |
62,32 |
|||||||||||
|
24 |
9,45 |
977,08 |
89,30 |
9233,41 |
843,91 |
7974,94 |
87255,69 |
6,88 |
65,06 |
|||||||||||
|
25 |
9,55 |
999,54 |
91,20 |
9545,61 |
870,98 |
8317,90 |
91160,55 |
6,91 |
65,96 |
|||||||||||
|
26 |
129,88 |
9644,21 |
877,63 |
75014,05 |
6600,48 |
52930,39 |
609485,41 |
121,38 |
766,60 |
|||||||||||
С |
У |
М |
М |
Ы |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
Поясним как таблица 2 составляется:
Шаг 1. В ячейки A1:A25 заносим значения ![]() .
.
Шаг 2. В ячейки B1:B25 заносим значения ![]() .
.
Шаг 3. В ячейку C1 вводим формулу =A1^2.
Шаг 4. В ячейки C2:C25 эта формула копируется.
Шаг 5. В ячейку D1 вводим формулу =A1*B1.
Шаг 6. В ячейки D2:D25 эта формула копируется.
Шаг 7. В ячейку E1 вводим формулу =A1^3.
Шаг 8. В ячейки E2:E25 эта формула копируется.
Шаг 9. В ячейку F1 вводим формулу =A1^4.
Шаг 10. В ячейки F2:F25 эта формула копируется.
Шаг 11. В ячейку G1 вводим формулу =A1^2*B1.
Шаг 12. В ячейки G2:G25 эта формула копируется.
Шаг 13. В ячейку H1 вводим формулу =LN(B1).
Шаг 14. В ячейки H2:H25 эта формула копируется.
Шаг 15. В ячейку I1 вводим формулу =A1*LN(B1).
Шаг 16. В ячейки I2:I25 эта формула копируется.
Последующие шаги делаем с помощью
автосуммирования ![]() .
.
Шаг 17. В ячейку A26 вводим формулу =СУММ(A1:A25).
Шаг 18. В ячейку B26 вводим формулу =СУММ(B1:B25).
Шаг 19. В ячейку C26 вводим формулу =СУММ(C1:C25).
Шаг 20. В ячейку D26 вводим формулу =СУММ(D1:D25).
Шаг 21. В ячейку E26 вводим формулу =СУММ(E1:E25).
Шаг 22. В ячейку F26 вводим формулу =СУММ(F1:F25).
Шаг 23. В ячейку G26 вводим формулу =СУММ(G1:G25).
Шаг 24. В ячейку H26 вводим формулу =СУММ(H1:H25).
Шаг 25. В ячейку I26 вводим формулу =СУММ(I1:I25).
Аппроксимируем функцию ![]() линейной функцией
линейной функцией ![]() . Для определения коэффициентов
. Для определения коэффициентов ![]() и
и ![]() воспользуемся
системой (4). Используя итоговые суммы таблицы 2, расположенные в ячейках A26, B26, C26 и D26, запишем систему (4) в виде:
воспользуемся
системой (4). Используя итоговые суммы таблицы 2, расположенные в ячейках A26, B26, C26 и D26, запишем систему (4) в виде:
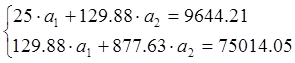 (11)
(11)
Решив которую, получим ![]() =
-252,14127 и
=
-252,14127 и ![]() = 122,78828 .
= 122,78828 .
Таким образом, линейная аппроксимация имеет вид:
![]() (12)
(12)
Решение системы (11) проводили, пользуясь средствами Microsoft Excel. Результаты представлены в таблице 3.
Таблица 3.
|
A |
B |
C |
D |
E |
|
|
28 |
25 |
129,88 |
9644,21 |
||
|
29 |
129,88 |
877,63 |
75014,05 |
||
|
30 |
|||||
|
31 |
Обратная матрица |
||||
|
32 |
0,17304 |
-0,02561 |
a1= |
-252,14127 |
|
|
33 |
-0,02561 |
0,00493 |
a2= |
122,78828 |
|
В таблице 3 в ячейках A32:B33 записана формула {=МОБР(A28:B29
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.