Аппроксимация функции методом наименьших квадратов. Вычисление коэффициентов детерминированности и корреляции

Анализ расчетов показывает, что квадратичная аппроксимация наилучшим образом описывает экспериментальные данные.

4. Представление результатов в графической форме

Выделим интервал A11 :В35.

При помощи “Мастера диаграмм” необходимо выбрать тип “XY-точечная” и первый тип авто формата.

Затем указать соответствующие параметры для диаграммы (подписать оси, назвать диаграмму и т.д.).

Для построения линии тренда щелкнуть по одной из точек графика. В появившемся окне выбрать “Вставка/Линия тренда”, затем в появившемся диалоговом окне выбрать соответствующий тип тренда.

В этом же окне перейти ко вкладке "Параметры" , указать уравнение тренда на диаграмме и показать значение R².

На диаграмме появится линия тренда с соответствующим уравнением, а также изменится легенда.

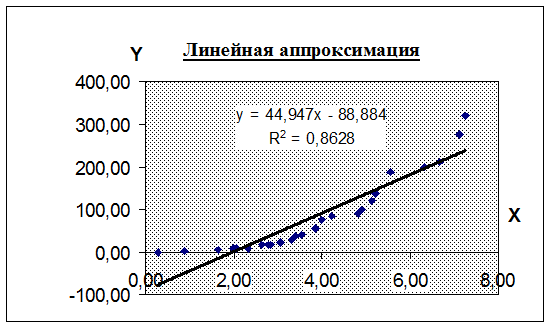
Рис.1. График линейной аппроксимации.

Для построения тренда квадратичной аппроксимации в типе тренда выбираем “полиномиальный/степень 2”.

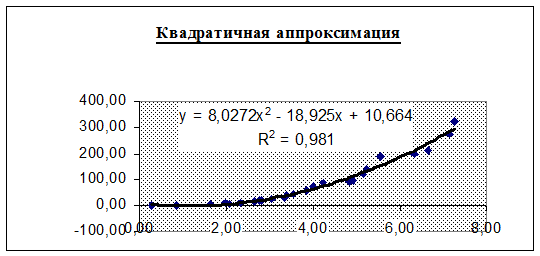Рис.2. График квадратичной аппроксимации.

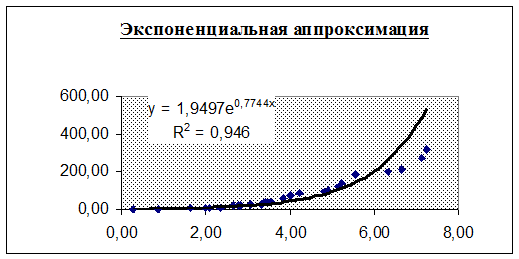
Рис.3. График экспоненциальной аппроксимации.

По полученным уравнениям, представленным в графической форме, можно сделать вывод, что все виды аппроксимации хорошо описывают экспериментальные данные. Все коэффициенты детерминированности близки к 1: для линейной аппроксимации R²=0,8628, для квадратичной – R²=0,981,  для экспоненциальной – R²=0,946, но квадратичная аппроксимация  наиболее точно отражает зависимость между эмпирическими значениями x и y. Графики дают наглядные представления о      приближении  полученных функций к экспериментальным данным.

Примечание. Полученное при построении линии тренда значение коэффициента детерминированности для экспоненциальной зависимости не совпадает со значением, полученным ранее.

5. Вычисления с помощью функции «ЛИНЕЙН»

Для получения результатов необходимо создать табличную формулу, которая будет занимать 5 строк и 2 столбца. Этот интервал может располагаться в произвольном месте на рабочем листе. В этот интервал требуется ввести функцию ЛИНЕЙН. Для этого выполняем следующую последовательность действий .

1.Вызываем Мастер функций.

2.Выбираем функцию ЛИНЕЙН.

3.Определяем аргументы функции

-В качестве изв_знач_уукажем В11:В35.

-В качестве изв_знач_хукажемА11:А35.

-Третье поле Константа оставляем пустым.

-В четвертом поле стат набираем истина.

4.Нажимаем кнопку Закончить.

5.Установим курсор в строку формул.

6.Нажмем комбинацию клавишCtrl+Shift+Enter,это обеспечивает ввод табличнойформулы.

В результате должны заполниться все ячейки интервала N2:O6.

         Функция «ЛИНЕЙН» позволяет вычислить некоторые параметры и статистические характеристики линии, которая наилучшим образом аппроксимирует имеющиеся данные. Функция возвращает массив, в котором  представлены линейные характеристики этой прямой. 

Результат работы этой функции отображен в следующей таблице.

Таблица 9

Числовые характеристики зависимости

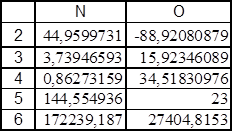N2 — коэффициент a₂ ;

O2 — коэффициент a₁;

N3 — стандартные значения ошибок для коэффициента a₂;

O3 — стандартные значения ошибок для коэффициента a₁;

N4 — коэффициент детерминированности;

O4 — стандартная ошибка для оценки y;

N5 — F – наблюдаемое значение;

O5 — число степеней свободы;

N6 — регрессионная сумма квадратов;

O6 — остаточная сумма квадратов.

Сравнивая  результаты, полученные при  помощи  функции  ЛИНЕЙН, видим, что они полностью совпадают с вычислениями коэффициентов линейной аппроксимации, найденными выше. Это указывает на то, что вычисления верны.

6. Выполнение расчета в среде Turbo Pascal 7.0

6.1. Алгоритм.

 Программа.

 

1.

См. приложение

2.

3.

См. приложение

4.     

5.

6.

7.

8.

9.

См. приложение

 

10.                                                                                          

См. приложение

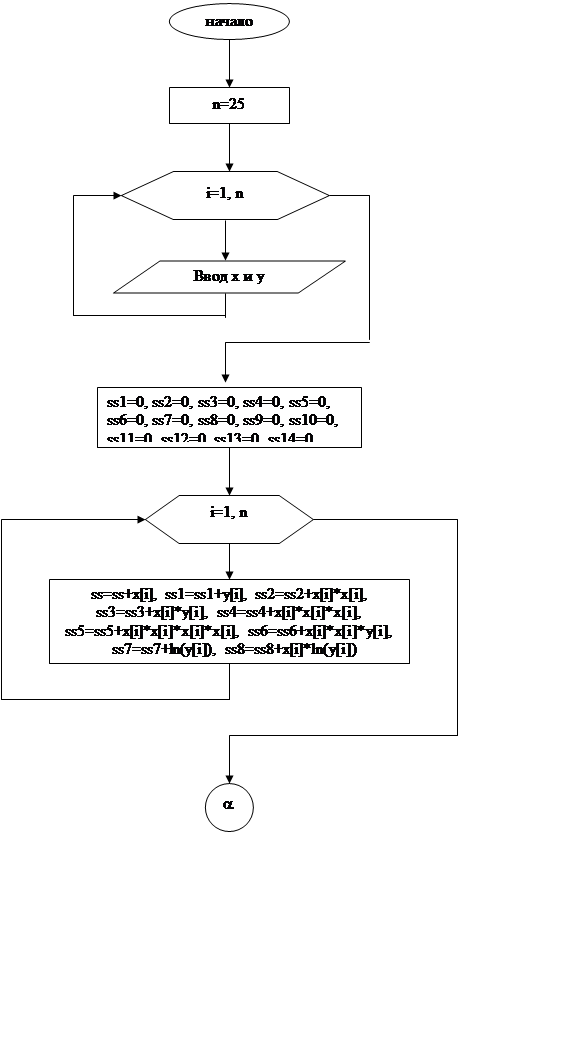
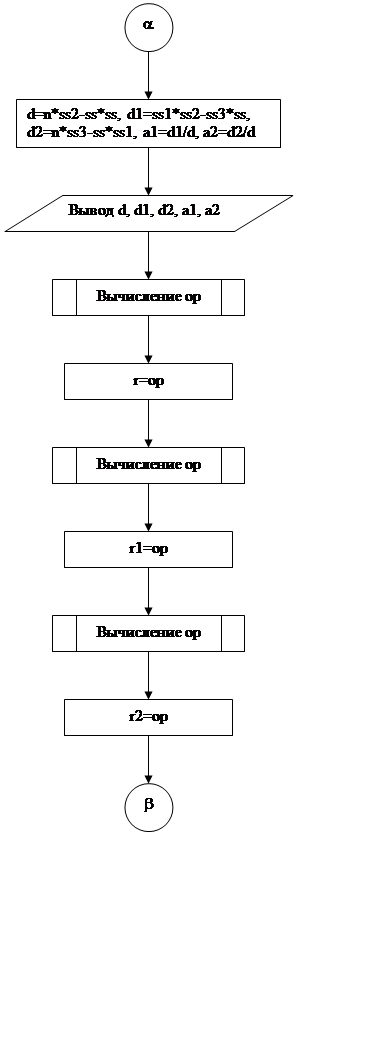
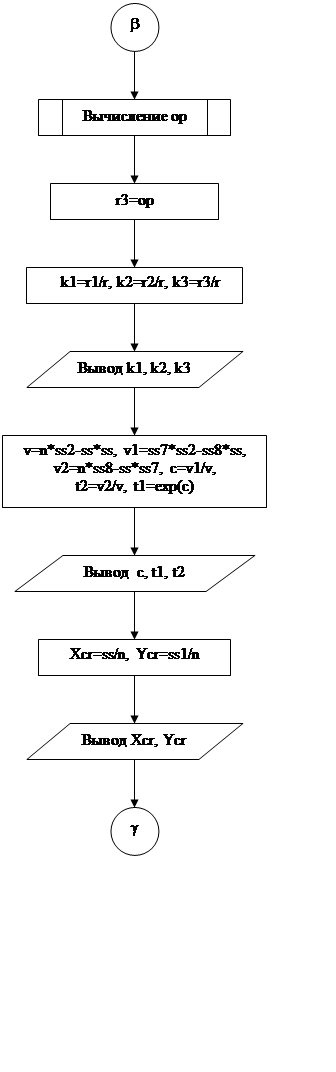
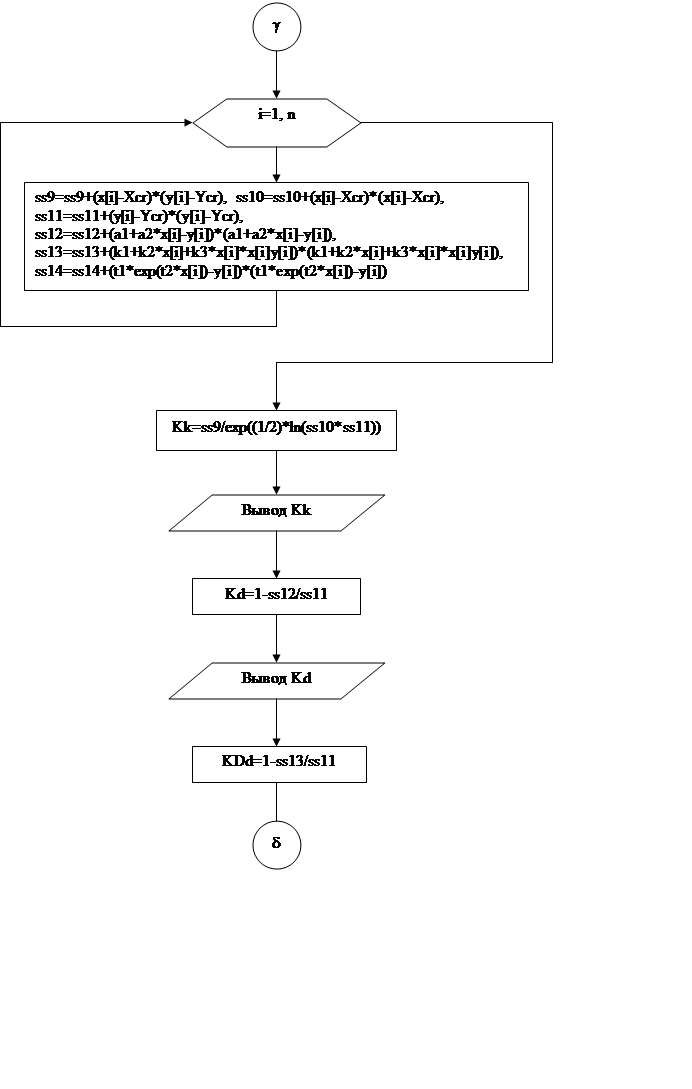
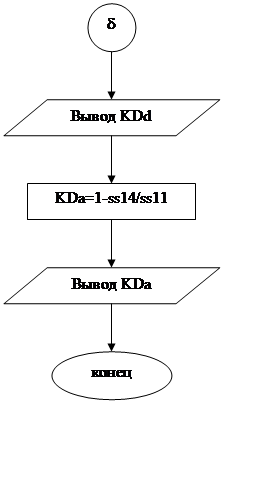
Рис.4 Блок-схема программы

Подпрограмма

                                                          

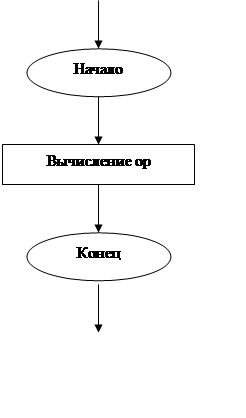
Вход в процедуру

11.

См. приложение

                                                  Выход из процедуры

Рис 5. Блок – схемам процедуры opred

6.2. Программа с необходимыми комментариями.

PROGRAM KR; {Начало программы}

uses crt;

type

vect=array[1..25] of real;

var {Заголовок раздела описания переменных}

x,y,s,s1,s2,s3,s4,s5,s6,s7,s8,s9,s10,s11,s12,s13,s14:vect;

ss,ss1,ss2,ss3,ss4,ss5,ss6,ss7,ss8,ss9,ss10,ss11,ss12,ss13,ss14:real;

r,r1,r2,r3,k1,k2,k3,x11,x12,x13,x21,x22,x23,x31,x32,x33,op,d,d1,d2:real;

a1,a2,v,v1,v2,t1,t2,c,Xcr,Ycr,Kk,Kd,KDd,KDa:real;

n,i:integer;

inf:text;

{Подпрограмма процедуры, вычисляющая определителя матрицы 3*3}

procedure opred(x11,x12,x13,x21,x22,x23,x31,x32,x33:real;var op:real);

begin    {Начало операторной части подпрограммы}

op:=0;

op:=(x11*x22*x33+x12*x23*x31+x13*x21*x32)(x13*x22*x31+x11*x23*x32+X12*x21*x33);

end;     {Конец операторной части подпрограммы}

begin    {Начало операторной части программы}

clrscr;

{Обнуление переменных}

ss:=0; ss1:=0; ss2:=0; ss3:=0; ss4:=0; ss5:=0; ss6:=0; ss7:=0;

ss8:=0; ss9:=0; ss10:=0; ss11:=0; ss12:=0; ss13:=0; ss14:=0;

assign(inf,'kr.txt');{Устанавливается связь файла данных kr.txt c

файловой переменной inf}

reset(inf);   {Файл kr.txt открывается для чтения}

FOR I:=1 to 25 do

read (inf,x[i],y[i]);

close(inf);  {Закрытие файла kr.txt для чтения}

FOR I:=1 TO 25 DO

begin

n:=25;

ss:=ss+x[i];      {Вычисление сумм}

ss1:=ss1+y[i];

ss2:=ss2+x[i]*x[i];

ss3:=ss3+x[i]*y[i];

ss4:=ss4+x[i]*x[i]*x[i];

ss5:=ss5+x[i]*x[i]*x[i]*x[i];

ss6:=ss6+x[i]*x[i]*y[i];

ss7:=ss7+ln(y[i]);

ss8:=ss8+x[i]*ln(y[i]);

end;

{Коэффициенты линейной функции}

d:=n*ss2-ss*ss;

d1:=ss1*ss2-ss3*ss;

d2:=n*ss3-ss*ss1;

a1:=d1/d;

a2:=d2/d;

writeln ('Коэффициенты линейной функции');

writeln ('a=',a1:10:4);

writeln ('a=',a2:10:4);

readln;

{Коэффициенты квадратичной функции}

x11:=n; x12:=ss; x13:=ss2; x21:=ss; x22:=ss2;

x23:=ss4; x31:=ss2; x32:=ss4; x33:=ss5;

opred(x11,x12,x13,x21,x22,x23,x31,x32,x33,op);

r:=op;

x11:=ss1; x12:=ss; x13:=ss2; x21:=ss3; x22:=ss2;

x23:=ss4; x31:=ss6; x32:=ss4; x33:=ss5;

opred(x11,x12,x13,x21,x22,x23,x31,x32,x33,op);

r1:=op;

x11:=n; x12:=ss1; x13:=ss2; x21:=ss; x22:=ss3;

x23:=ss4; x31:=ss2; x32:=ss6; x33:=ss5;

opred(x11,x12,x13,x21,x22,x23,x31,x32,x33,op);

r2:=op;

x11:=n; x12:=ss; x13:=ss1; x21:=ss; x22:=ss2;

x23:=ss3; x31:=ss2; x32:=ss4; x33:=ss6;

opred(x11,x12,x13,x21,x22,x23,x31,x32,x33,op);

r3:=op;

k1:=r1/r;

k2:=r2/r;

k3:=r3/r;

writeln ('Коэффициенты квадратичной функции');

writeln ('k1=',k1:10:4);

writeln ('k2=',k2:10:4);

writeln ('k3=',k3:10:4);

readln;

{Коэффициенты экспоненциальной функции}

v:=n*ss2-ss*ss;

v1:=ss7*ss2-ss8*ss;

v2:=n*ss8-ss*ss7;

c:=v1/v;

t2:=v2/v;

writeln ('Коэффициенты экспоненциальной функции');

writeln ('c=',c:10:4);

writeln ('t2=',t2:10:4);

t1:=exp(c);

writeln ('t1=',t1:10:4);

Xcr:=ss/n;

Ycr:=ss1/n;

writeln;

writeln ('Xcr=',Xcr:10:4);

writeln ('Ycr=',Ycr:10:4);

readln;

FOR I:=1 TO 25 DO

begin

ss9:=ss9+(x[i]-Xcr)*(y[i]-Ycr);     {Вычисление сумм}

ss10:=ss10+(x[i]-Xcr)*(x[i]-Xcr);

ss11:=ss11+(y[i]-Ycr)*(y[i]-Ycr);

ss12:=ss12+(a1+a2*x[i]-y[i])*(a1+a2*x[i]-y[i]);

ss13:=ss13+(k1+k2*x[i]+k3*x[i]*x[i]-y[i])*(k1+k2*x[i]+k3*x[i]*x[i]-y[i]);

ss14:=ss14+(t1*exp(t2*x[i])-y[i])*(t1*exp(t2*x[i])-y[i]);

end;

Kk:=ss9/exp((1/2)*ln(ss10*ss11)); {вычисление коэффициента корреляции}

writeln ('Коэффициент кореляции Kk=',Kk:8:5);

Kd:=1-ss12/ss11; {вычисление коэф. детер. (лин. аппрок.)}

writeln ('Коэффициент детерминированности (лин.аппрок.) Kd=',Kd:8:5);

KDd:=1-ss13/ss11;{вычисление коэф. детер. (квад. аппрок.)}

writeln ('Коэффициент детерминированности (квадр. аппрок.) KDd=',KDd:8:5);

KDa:=1-ss14/ss11;{вычисление коэф. детер. (эксп. аппрок.)}

writeln ('Коэффициент детерминированности (эксп. аппрок.) KDa=',KDa:8:5);

readln;

end. {Конец операторной части программы}