Делаем аналогичные расчеты и для Yi
ymin= 25,66
ymax= 78,50
![]()
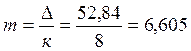 – шаг
интервала где, к – число интервалов равное
8
– шаг
интервала где, к – число интервалов равное
8
Находим частоту попадания случайных величин в каждый из интервалов и составляем вспомогательную таблицу 3., для построения гистограмм.
Таблица 3
|
Интервалы Yi |
ni |
Σ ni |
Pi |
ΣPi |
|
|
78,50 |
71,90 |
7 |
7 |
0,14 |
0,14 |
|
71,90 |
65,29 |
7 |
14 |
0,14 |
0,28 |
|
65,29 |
58,69 |
8 |
22 |
0,16 |
0,44 |
|
58,69 |
52,08 |
11 |
33 |
0,22 |
0,66 |
|
52,08 |
45,48 |
10 |
43 |
0,2 |
0,86 |
|
45,48 |
38,87 |
1 |
44 |
0,02 |
0,88 |
|
38,87 |
32,27 |
3 |
47 |
0,06 |
0,94 |
|
32,27 |
25,66 |
3 |
50 |
0,06 |
1 |
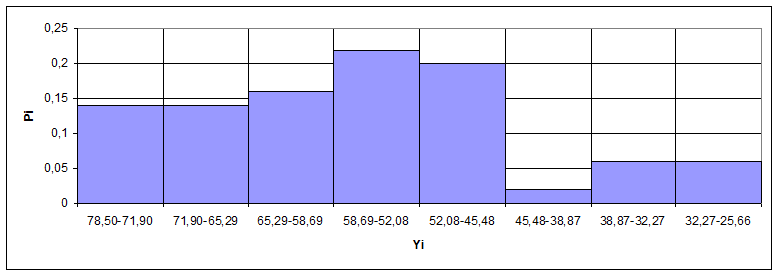
Рис.3 Гистограмма распределения Yi от Pi
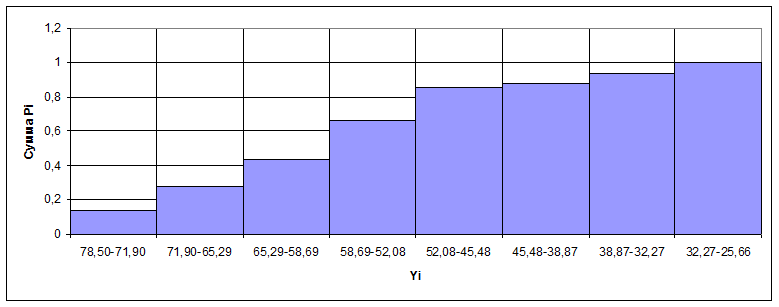
Рис.4 Гистограмма
распределения Yi от ![]()
II. Получение начальных и центральных моментов выборочного
распределения
Начальные моменты выборочного распределения рассчитываются по формуле:
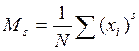 , где Ms - начальный момент s-го порядка;
, где Ms - начальный момент s-го порядка;
xi - i-ое значение величины, i=1,2,…N.
Центральные моменты рассчитываются по формуле:
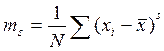 , где ms - центральный момент s-го порядка;
, где ms - центральный момент s-го порядка;
![]() среднее
арифметическое,
среднее
арифметическое, 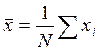 . (начальный момент
первого порядка).
. (начальный момент
первого порядка).
Наиболее часто на практике используется центральный момент второго порядка (оценка дисперсии):
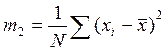 , а также
, а также ![]() (среднее
квадратичное отклонение).
(среднее
квадратичное отклонение).
Для оценки формы кривой распределения используются центральные моменты третьего и четвертого порядков, которые высчитываются по формулам:
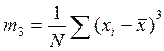 ;
;
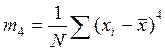 ,
,
Значение начальных и центральных моментов (для Хi)
Таблица 4
|
М1 |
М2 |
М3 |
М4 |
m1 |
m2 |
m3 |
m4 |
|
21,958 |
560,766 |
16697,984 |
570017,910 |
0,000 |
78,612 |
932,362 |
28235,869 |
Для оценки степени асимметрии распределения используется коэффициент асимметрии:
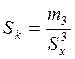 ,
,
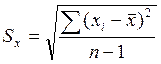
а для оценки характеристики степени “крупности” - показатель эксцесса:
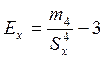 ,
,
Для оценки близости распределения к нормальному рассчитываются вспомогательные коэффициенты:
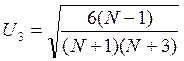 и
и 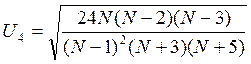 .
.
Если ![]() ,
а
,
а ![]() соблюдается, то закон
распределения можно считать нормальным.
соблюдается, то закон
распределения можно считать нормальным.
По расчету получается:
Таблица 5
|
Sx |
Sk |
Ex |
U3 |
U4 |
|
8,956 |
1,298 |
1,388 |
0,330 |
0,622 |
Вывод: Т.к. условия ![]() , а
, а ![]() не
соблюдается, то закон распределения можно считать ненормальным.
не
соблюдается, то закон распределения можно считать ненормальным.
Значение начальных и центральных моментов (для Yi)
Таблица 6
|
М1 |
М2 |
М3 |
М4 |
m1 |
m2 |
m3 |
m4 |
|
56,673 |
3393,698 |
211842,675 |
13659673,989 |
0,000 |
181,892 |
-1104,311 |
89107,146 |
Для оценки степени асимметрии распределения используется коэффициент асимметрии:
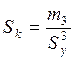 ,
,
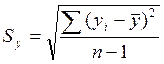
а для оценки характеристики степени “крупности” - показатель эксцесса:
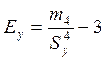 ,
,
Для оценки близости распределения к нормальному рассчитываются вспомогательные коэффициенты:
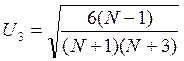 и
и 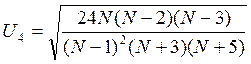 .
.
Если ![]() ,
а
,
а ![]() соблюдается, то закон
распределения можно считать нормальным.
соблюдается, то закон
распределения можно считать нормальным.
По расчету получается:
Таблица 7
|
Sx |
Sk |
Ex |
U3 |
U4 |
|
13,624 |
-0,437 |
-0,413 |
0,330 |
0,622 |
Вывод: Т.к. условия ![]() , а
, а ![]() соблюдается,
то закон распределения можно считать нормальным.
соблюдается,
то закон распределения можно считать нормальным.
III. Получение коэффициента корреляции
Вычисление коэффициента корреляции удобно производить по следующей формуле:
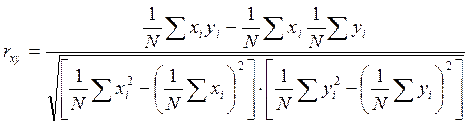 .
.
Таблица 8
|
N |
SXi |
SYi |
SXiYi |
SX2i |
SY2i |
|
50 |
1097,900 |
2833,640 |
57042,300 |
28038,290 |
169684,897 |
rxy= -0,86617
IV. Нахождение теоретической линии регрессии
Для нахождения по методу наименьших квадратов коэффициентов линейного уравнения Y=a+bx можно воспользоваться следующими формулами:
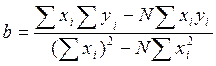 ;
; 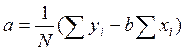
|
b |
a |
|
-1,318 |
85,604 |
Остаточная дисперсия рассчитывается по формуле:
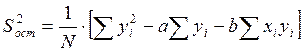
![]()
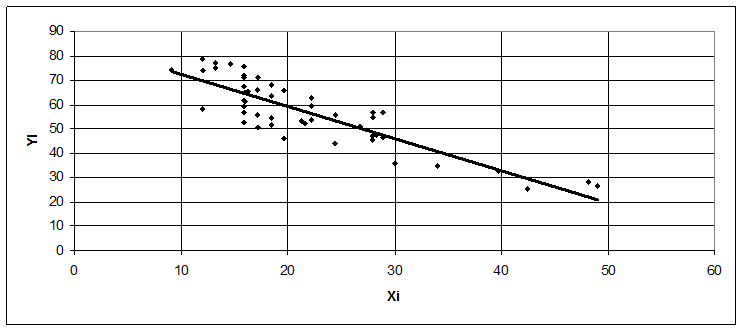
Рис.5 Линия регрессии
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.