




















































разложение общего вида функции ![]() получим, используя уже
вычисленные коэффициенты. Продолжим сначала функцию
получим, используя уже
вычисленные коэффициенты. Продолжим сначала функцию ![]() нулем
на полуинтервал
нулем
на полуинтервал ![]() :
:
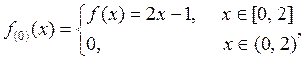
а затем рассмотрим периодическое продолжение ![]() функции
функции ![]() на
всю числовую ось (оно же будет периодическим продолжением функции
на
всю числовую ось (оно же будет периодическим продолжением функции ![]() ) (рис. 3.4). Поскольку
) (рис. 3.4). Поскольку 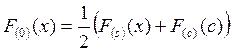 , то значит ее разложение в ряд
Фурье
, то значит ее разложение в ряд
Фурье
![]() ,
, ![]() , где
, где
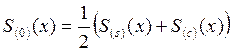 ,
, ![]() , то есть функция
, то есть функция ![]() раскладывается
в ряд Фурье по синусам и косинусам:
раскладывается
в ряд Фурье по синусам и косинусам:
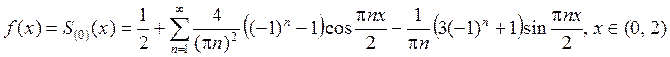 .
.
При этом
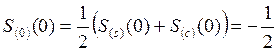 ,
, 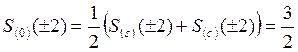 .
.
График суммы ряда Фурье ![]() изображен
на рис. 3.5.
изображен
на рис. 3.5.
|
|
|
|
рис. 3.4 |
рис. 3.5 |
4. Теория функций комплексного переменного. Операционное исчисление
4.1. Комплексные числа
Комплексным
числом ![]() называется
арифметическое выражение вида
называется
арифметическое выражение вида
|
|
(4.1) |
где ![]() -
действительные числа, а
-
действительные числа, а ![]() - специальный
символ, который называется мнимой единицей. Для мнимой единицы по
определению считается, что
- специальный
символ, который называется мнимой единицей. Для мнимой единицы по
определению считается, что ![]() .
.
(4.1) – алгебраическая форма
комплексного числа, причем ![]() называется действительной
частью комплексного числа, а
называется действительной
частью комплексного числа, а ![]() - мнимой
частью.
- мнимой
частью.
Число ![]() называется
комплексно сопряженным к числу
называется
комплексно сопряженным к числу ![]() .
.
Пусть даны два комплексных числа ![]() ,
, ![]() .
.
1. Суммой ![]() комплексных
чисел
комплексных
чисел ![]() и
и ![]() называется
комплексное число
называется
комплексное число
![]() .
.
2. Разностью ![]() комплексных
чисел
комплексных
чисел ![]() и
и ![]() называется
комплексное число
называется
комплексное число
![]() .
.
3. Произведением ![]() комплексных чисел
комплексных чисел ![]() и
и ![]() называется
комплексное число
называется
комплексное число
![]() .
.
4. Частным ![]() от
деления комплексного числа
от
деления комплексного числа ![]() на
комплексное число
на
комплексное число ![]() называется комплексное
число
называется комплексное
число
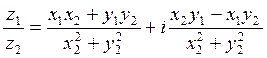 .
.
Замечание 4.1. То есть операции над комплексными числами вводятся по обычным правилам арифметических операций над буквенными выражениями в алгебре.
Пример 4.1. Даны
комплексные числа ![]() . Найти
. Найти
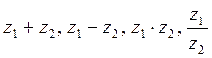 .
.
Решение. 1)![]() .
.
2)![]() .
.
3) ![]()
![]() .
.
4) Домножая числитель и знаменатель на комплексно сопряженное знаменателю число, получаем
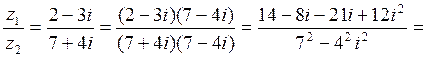
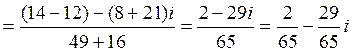 .
.
Тригонометрическая формакомплексного числа:
![]() , где
, где ![]() - модуль
комплексного числа,
- модуль
комплексного числа, ![]() - аргумент
комплексного числа. Угол
- аргумент
комплексного числа. Угол ![]() определен
неоднозначно, с точностью до слагаемого
определен
неоднозначно, с точностью до слагаемого ![]() :
:
![]() ,
, ![]() .
.
![]() - главное
значение аргумента, определяемое условием
- главное
значение аргумента, определяемое условием
![]() , (или
, (или ![]() ).
).
Показательная форма комплексного числа:
![]() .
.
Корень ![]() й степени числа
й степени числа ![]() имеет
имеет
![]() различных значений, которые
находятся по формуле
различных значений, которые
находятся по формуле
|
|
(4.2) |
где ![]() .
.
Точки, соответствующие значениям ![]() , являются вершинами правильного
, являются вершинами правильного ![]() угольника, вписанного в
окружность радиуса
угольника, вписанного в
окружность радиуса ![]() с центром в начале
координат.
с центром в начале
координат.
Пример 4.2. Найти
все значения корня ![]() .
.
Решение. Представим
комплексное число ![]() в тригонометрической
форме:
в тригонометрической
форме:
![]() ,
,
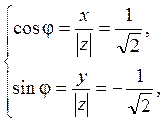 , откуда
, откуда 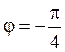 .
.
Тогда 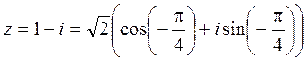 .
Следовательно, по формуле (4.2)
.
Следовательно, по формуле (4.2) ![]() имеет четыре
значения:
имеет четыре
значения:
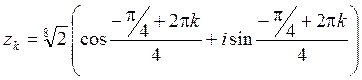 ,
, ![]() .
.
Полагая
![]() , находим
, находим
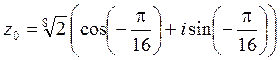 ,
, 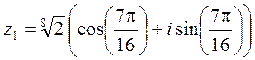 ,
,
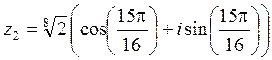 ,
, 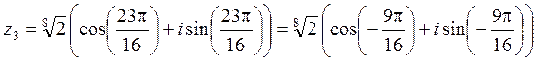 .
.
Здесь мы преобразовывали значения аргумента к его главному значению.
Множества на комплексной плоскости
Комплексное число ![]() изображается на плоскости
изображается на плоскости ![]() точкой
точкой ![]() с координатами
с координатами ![]() . Модуль
. Модуль ![]() и аргумент
и аргумент ![]() соответствуют полярным
координатам точки
соответствуют полярным
координатам точки ![]() .
.
Полезно помнить, что неравенство ![]() задает круг с центром в точке
задает круг с центром в точке ![]() радиуса
радиуса ![]() . Неравенство
. Неравенство ![]() задает полуплоскость,
расположенную правее прямой
задает полуплоскость,
расположенную правее прямой ![]() , а неравенство
, а неравенство
![]() - полуплоскость, расположенную
выше прямой
- полуплоскость, расположенную
выше прямой ![]() . Кроме того, система неравенств
. Кроме того, система неравенств ![]() задает угол между лучами
задает угол между лучами ![]() и
и ![]() ,
выходящими из начала координат.
,
выходящими из начала координат.
Пример 4.3. Нарисовать
область, заданную неравенствами: 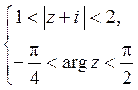 .
.
Решение. Первому
неравенству соответствует кольцо с центром в точке ![]() и
двумя радиусами 1 и 2, окружности в область не входят (рис. 4.1).
и
двумя радиусами 1 и 2, окружности в область не входят (рис. 4.1).
Второму неравенству соответствует
угол между лучами 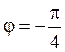 (биссектриса 4 координатного
угла) и
(биссектриса 4 координатного
угла) и 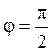 (положительное направление оси
(положительное направление оси ![]() ). Сами лучи в область не входят
(рис. 4.2).
). Сами лучи в область не входят
(рис. 4.2).
Искомая область является пересечением двух полученных областей (рис. 4.3)
|
|
|
|
|
рис. 4.1 |
рис. 4.2 |
рис. 4.3 |
4.2. Функции комплексного переменного
Пусть однозначная
функция ![]() определена и непрерывна в
области
определена и непрерывна в
области ![]() , а
, а ![]() -
кусочно-гладкая замкнутая или незамкнутая ориентированная кривая, лежащая в
-
кусочно-гладкая замкнутая или незамкнутая ориентированная кривая, лежащая в ![]() . Пусть, как обычно,
. Пусть, как обычно, ![]() ,
, ![]() ,
где
,
где ![]() ,
, ![]() -
действительные функции переменных
-
действительные функции переменных ![]() и
и ![]() .
.
Вычисление интеграла от функции ![]() комплексного переменного
комплексного переменного ![]() сводится к вычислению обычных
криволинейных интегралов, а именно
сводится к вычислению обычных
криволинейных интегралов, а именно
|
|
(4.3) |
Если функция ![]() аналитична в односвязной области
аналитична в односвязной области
![]() , содержащей точки
, содержащей точки ![]() и
и ![]() ,
то имеет место формула Ньютона-Лейбница:
,
то имеет место формула Ньютона-Лейбница:
|
|
(4.4) |
где ![]() - какая-либо
первообразная для функции
- какая-либо
первообразная для функции ![]() , то есть
, то есть ![]() в области
в области ![]() .
.
В интегралах от функций комплексного переменного можно производить
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.