Элементы теории графов. Три изображения одного и того же графа. Локальные степени. Локальные степени для ориентированного графа

Элементы теории графов

Определение 1

Пусть V – конечное множество (множество вершин), А – множество  упорядоченных пар вершин, элементы которого называются ребрами. Тогда графом G(V,A) называется совокупность множества вершин и множества ребер. Вершины а и с соединяются ребром, если (а, с)ÌА.

Определение 2

Пусть дано множество вершин V и декартово произведение VхV – множество всевозможных пар вершин. Тогда графом G является подмножество декартового произведения.

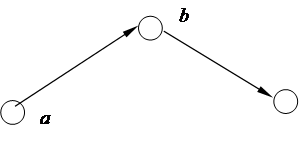
·  Ребро графа G ориентировано, если порядок пары (a,b) существенен.

·  Ребро графа G не ориентировано, если порядок пары (a,b) несущественен.

					Ориентированный граф
			c

 

·  Граф называется ориентированным, если все его ребра ориентированы.

·  Граф G называется неориентированным, если все его ребра неориентированы.

·  Смешанным графом называется граф, у которого есть как ориентированные, так и неориентированные ребра.

Каждому ребру E=ía,bý можно поставить в соответствие некоторое число

·  Граф G, каждому ребру которого присвоено число (например расстояние), называется сетью.

·  Пусть даны a,b – вершины графа. Ребро E их соединяет. Тогда говорят, что ребро E инцидентно вершинам a и b. И обратно – вершины a и b инцидентны ребру E.

При изображении графа имеется большая свобода в размещении вершин и дуг.

b

a

a

c

d

 

Три изображения одного и того же графа

Определение 3

Пусть G и G₁ – графы, V и V₁ – множества их вершин соответственно. Графы G и G₁ изоморфны, если существует взаимно однозначное соответствие между множествами их вершин V и V₁ и вершины в графе G соединены ребром в том и только том случае, если соответствующие вершины соединены ребром в графе G₁.

·  Если графы G и G₁ ориентированы, то направления ребер должны соответствовать друг другу. Изоморфные графы имеют одинаковые свойства.

·  Вершина, не инцидентная никакому ребру, называется изолированной. Граф, состоящий из изолированных вершин, называется “нуль-граф”. Обозначается через О.

·  Граф, две любые вершины которого соединены ребром, называется полным графом U=U(V).

·  Петлей называется ребро L=(a,a). Петля считается неориентированным ребром.

					петля
	b

 

·  Пара вершин может соединяться несколькими различными ребрами.

Пара ребер E_iE_jориентированная в противоположном направлении, эквивалентна одному неориентированному ребру.

Таким образом, мы можем любой неориентированный граф превратить в ориентированный. При этом количество ребер увеличивается в 2 раза.

Для каждого ориентированного графа G существует:

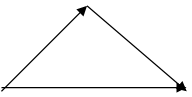
1)  обратный граф G*, получаемый из G изменением ориентации ребер;

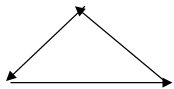
2)  соотнесенный неориентированный граф G_n, ребрами которого являются ребра графа G, но уже без ориентации.

 

G                                     G*                                   G_n

·  Граф называется плоским, если может быть изображен на плоскости так, чтобы его ребра пересекались только в вершинах.

Локальные степени

·  Граф G называется конечным, если число его ребер конечно.

·  Граф называется бесконечным, если число его ребер бесконечно.

·  Пусть G – конечный граф. Число ребер, инцидентных вершине а, называется локальной степенью графа в вершине а и обозначается r(a)

Обозначим   r(a,b)  число ребер,  соединяющих  вершины   a и b.

Тогда r(a, b)=r(b,a).

Если в G нет кратных ребер, то имеем

b1

r(a,b)=1, если вершины a и b соединены,

            0, если вершины a и b не соединены.

	b2

 

	bn

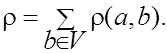
·  Обозначим число ребер в графе G через .

Тогда

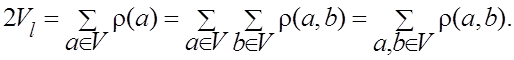
Множитель 2 появляется, т.к. каждое ребро учитывается в двух локальных степенях.

Так как левая часть формулы – четное число, то и правая часть – тоже четное число. Удалим из правой части все вершины с четными локальными степенями. Обозначим a₁ – вершины с нечетными локальными степенями и рассмотрим

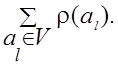
Это четное число (как разность четных чисел); r(a₁) – нечетные числа