Определение момента количества движения. Оператор орбитального момента: по принципу соответствия

Вывод: степень вырождения выше, чем в общем случае центрального поля.

8.  Теоремы Эренфеста:

для средних значений квантовых величин верны аналоги уравнений классической механики.

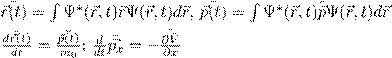
9.  Понятие минимизирующего волнового пакета (?): наиболее узкий (насколько позволяет соотношение неопределенностей) волновой пакет:

10.  Понятие когерентного состояния (?):

частный случай состояния квантового гармонического осциллятора, наиболее близкое к состоянию классического осциллятора (в том смысле, что выполняется соотношение ): волновой пакет сохраняет свою ширину (не расползается со временем), а его центр движется по классической траектории.

11.  Формулировка квазиклассических условий квантования: правило Бора-Зоммерфельда - квантование площади кривой в фазовом пространстве:

условие применимости:  или.

12.  Физические предпосылки уравнения Дирака (?): необходимо уравнение, инвариантное относительно преобразований Лоренца.

13.  Уравнение Дирака:

,

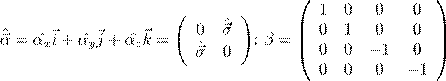
14.  Уравнение Паули: нерелятивистский предел уравнения Дирака.

 или

E  = m₀c² +E⁰ - полная релятивистская энергия,  - решение уравнения Дирака (4-х мерное).

15.  Уравнение неразрывности для уравнения Дирака:

 - уравнение неразрывности для уравнения Дирака, где - плотность вероятности, ~j = cΨ⁺α~ˆΨ - плотность потока вероятности.

16.  Частицы и дырки:

и те и другие используются в Дираковской модели вакуума, их состояния разделены некоторой энергетической щелью. Получаются из наличия двух (положительного и отрицательного) решений уравнения

Дирака.

частицы: ими заполнены все состояния с отрицательной энергией в вакууме; заполненный уровень положительной энергии воспринимается как частица (античастицы: свободные уровни с отрицательной энергией).

дырки: введены для удобства; свободный уровень с положительной энергией воспринимается как дырка; дырке в электронном вакууме соответствует позитрон.

17.  Спин-орбитальное взаимодействие: поправки, вводимые в Гамильтониан системы (не только С-О взаимодействие):

 - описывает релятивистскую зависимость массы от скорости;  Спин-орбитальное взаимодействие (равенство верно в случае центрального потенциала).

ˆ~ - спин, M^ˆ~ - орбитальный момент. Здесь ~ε - напряженность электрического поля; S

18.  Эффект Зеемана:

расщепление энергетических уровней в однородном магнитном поле. Простой (нормальный): перпендикулярно магнитному полю - 3 линейно-поляризованные компоненты (несмещенная (поляризована вдоль поля) и 2 имметричные смещенные (поляризованы перпендикулярно полю)); вдоль поля - 2 компоненты с круговой поляризацией. Без учета спина: расщепление на эквидистантные уровни (2l+1). В общем случае (аномальный эффект, с учетом спина): симметричная относительно немещенной компоненты картина из (2j+1) равноотстоящих линий, добавляется множитель Ландэ.

 - напряженность магнитного поля.

Применимость: общий случай - для малых полей (эффект мал по сравнению с тонкой структурой); бесспиновые частицы - для средних полей. Во всех случаях потенциал от времени не зависит. Первый порядок теории возмущений.

19.  Эффект Пашена - Бака:

эффект состоит в том, что в сильных магнитных потях аомальный эффект Зеемана переходит в простой (может перейти и не полностью). Рассмотренный пример: 4 уровня, 1 из них двукратно вырожден; система уровней эквидистантна.

 - напряженность магнитного поля.

Применимость: очень сильные магнитные поля (рассматриваем квадратичные приближения), вызывающие расщепление пропорциональное магнетону Бора и превышающее расщепление тонкой структуры.

20.  Эффект Штарка: расщепление уровней в однородном электрическом поле без учета спин-орбитального взаимодействия.

Квадратичный: Штарковские подуровни дважды вырождены (все, кроме J = 0), возможен в любом центральном поле; второй порядок теории возмущений. Симметричная картина расщепления.

Линейный: существует в Кулоновском поле; первый порядок теории возмущений; уровни эквидистантны.

21.  Различие эффектов Штарка в центральном и кулоновском полях:

Кулоновское поле: линейный эффект Штарка. Причина: наличие дополнительного вырождения по орбитальному квантовому числу.

Центральное поле: отсутствие линейного члена, квадратичный эффект Штарка.

22.  Формула вероятности перехода в единицу времени:

 - вероятность того, что в t система будет в состоянии m, если в начале