Расчёт коэффициента линейной парной корреляции. Теоретический коэффициент детерминации

Остаточная (необъясненная) дисперсия рассчитывается следующим образом:

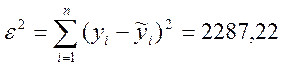
Для оценки качества полученного уравнения регрессии рассчитаем теоретический коэффициент детерминации – R²_yx:

,

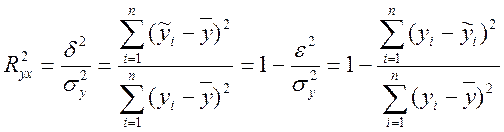Используя, полученные данные из таблицы 3 находим коэффициент:

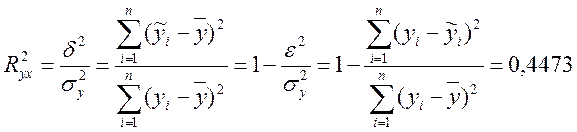
Следовательно, уравнение регрессии объясняется 44,7% дисперсии результативного признака, а на долю прочих факторов приходится 55,3% дисперсии (т.е. остаточная дисперсия).

3.  Оценить статистическую значимость уравнения регрессии в целом на пятипроцентном уровне  с помощью F-критерия Фишера. Сделать вывод.

При этом вычисляют фактическое (наблюдаемое) значение F-критерия, через коэффициент детерминации R²_y(x1,...,xm), рассчитанный по данным конкретного наблюдения:

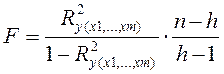, где n-число наблюдений; h – число оцениваемых параметров (в случае двухфакторной линейной регрессии h=3).

Следовательно,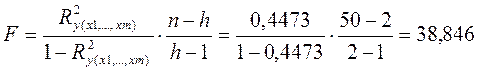  

Табличное значение F-критерия при уровне значимости 0,05 составит 3,21 (при =2; =45). Т.е. фактическое значение F превышает табличное, и можно сделать вывод, что дополнительное включение фактора  в модель статистически оправдано и коэффициент чистой регрессии  при факторе  статистически значим.

4.  Выполнить прогноз ожидаемого значения признака-результата y при прогнозном значении признака-фактора х, составляющим 105% от среднего уровня х. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал с вероятностью 0,95.

Прогнозируемое значение признака-результата c доверительной вероятностью равной 0,95 принадлежит интервалу прогноза:

(-t·m_p; +t·m_p), где - точечный прогноз результата, определяемый путем подстановки в модель регрессии ;

Затем точечный прогноз, млн.руб.

Коэффициент доверия в данном случае будет:

Среднеквадратическая ошибка регрессии будет равна:

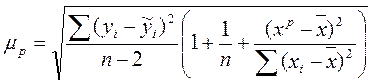=7,99.

Тогда доверительный интервал прогноза будет следующим:

, или

Т.е. при прогнозе увеличения собственных оборотных средств на 105% от своего среднего уровня с вероятностью 0,95 можно утверждать, что ожидаемое значение балансовой прибыли будет не ниже 113,37 и не выше 145,65 млн.руб.

Задание № 2

На основе данных, приведенных в Приложении и соответствующих варианту (таблица 4), требуется:

Построить уравнение множественной регрессии. При этом признак-результат и один из факторов остаются теми же, что и в первом задании. Выберите дополнительно еще один фактор из приложения 1 (границы наблюдения должны совпадать с границами наблюдения признака-результата, соответствующего варианту). При выборе фактора нужно руководствоваться  его экономическим содержанием или другими подходами. Пояснить смысл параметров уравнения.

Таблица 4. Исходные данные

Признак	Среднее значение	Среднее квадратичное отклонение	Линейный коэффициент парной корреляции
Собственные оборотные средства, млн.руб.    x1	1289,52	340,95	ryx1=0,669
Балансовая прибыль, млн.руб.    y	109,56	9,1	-
Дебиторская задолженность, млн.руб.    x2	49,36	14,28	ryx2=-0,72 rx1x2=-0,5

Линейное уравнение множественной регрессии y от x₁ и x₂ имеет вид:

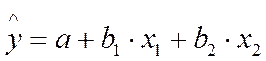
Для расчета его параметров применим метод стандартизации переменных и построим искомое уравнение в стандартизованном масштабе:

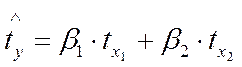
Стандартизированные частные коэффициенты регрессии – b_i показывают, на какую часть своего среднего квадратического отклонения s_у изменится признак-результат y, с изменением соответствующего фактора х_i на величину своего среднего квадратического отклонения (s_хi) при неизменном влиянии прочих факторов (входящих в уравнение).

Параметр b_i показывает, на сколько изменится  признак-результат y при изменении соответствующего фактора х_i. Параметр a отражает степень изменения y.

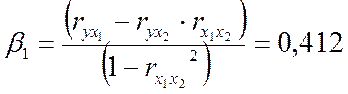
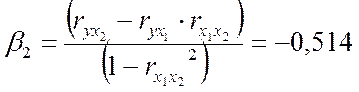
Получим уравнение:

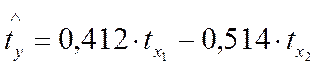
Из уравнения видно, что с ростом фактора х₁ на одну сигму при неизменном значении дебиторской задолжности балансовая прибыль увеличится в среднем на 0,412 сигмы. Так как , то можно утверждать , что большее влияние оказывает на балансовую прибыль фактор х₂.

Для построения уравнения рассчитаем b₁ и b₂

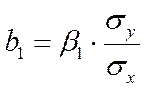
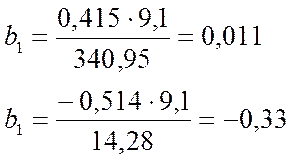
Значение а определим из соотношения:

Уравнение будет иметь вид:

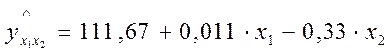
Видно, что при том же значении дебиторской задолжности, рост собственных оборотных средств на 1 млн. руб. повлечет за собой увеличение балансовой прибыли в среднем на 0.011 млн. руб.

А увеличение дебиторской задолжности на 1 млн. руб. при постоянном значении собственных оборотных средств  приведет к сокращению балансовой прибыли на 0,33 млн. руб.

Рассчитать частные коэффициенты эластичности. Сделать вывод.

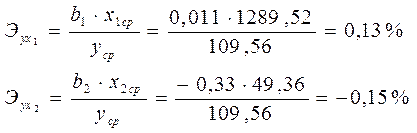
C увеличением собственных оборотных средств x₁ на 1% от ее среднего уровня балансовая прибыль увеличивается на 0,13% от своего среднего уровня. При повышении среднего значения дебиторской задолжности x₂ на 1% балансовая прибыль уменьшается на 0,15%.

Задание № 3

На основе данных, приведенных в таблице 5 и соответствующих варианту