Приобретение практических навыков оценки дисперсии генеральной совокупности по ГОСТ Р 50779.21-96

Лабораторная работа №7

Цель работы - приобретение практических навыков оценки дисперсии генеральной совокупности по ГОСТ Р 50779.21-96.

Квантили распределения

Квантилью, отвечающей уровню вероятности g, называют такое значение варианты xg, при котором функция распределения случайной величины принимает значение g, т. е. квантиль – это значение аргумента xg функции распределения, при котором F(xg)=g. Эмпирическую квантиль находят по заданному значению вероятности g, используя вариационный ряд или ступенчатую ломаную линию. Таким образом, квантили – это способ описать группу измерений. 

Квантиль  можно представить точкой  на  числовой  шкале,  которая  делит  совокупность наблюдений на группы с соответствующими пропорциями в каждой из них. Частные случаи квантилей: 

-  Медиана – делит наблюдение на две группы (квантиль порядка 0,5)      

-  Квартиль – делит наблюдения на 4 группы (квантиль порядка 0,25)

-  Дециль – делит наблюдения на 10 групп (квантиль порядка 0, 1)

-  Квинтель – делит наблюдения на 5 групп (квантиль порядка 0,2)

-  Процентиль – делит наблюдения на 100 групп (квантиль порядка 0,01).

«Хи-квадрат» распеделение с f степенями свободы, распределение вероятностей суммы квадратов

 = X₁²+...+X_f²,

независимых случайных величин X₁,..., X_f, подчиняющихся нормальному распределению с нулевым математическим ожиданием и единичной дисперсией. Функция «Хи-квадрат» распеделение выражается интегралом

,

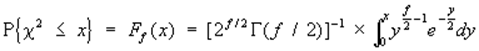  Первые три момента (математическое ожидание дисперсия и третий центральный момент) суммы равны соответственно f, 2f, 8f.

Сумма двух независимых случайных величин и , с f₁ и f₂ степенями свободы подчиняется «Хи-квадрат» распеделению с f₁ + f₂ степенями свободы.

Если количество слагаемых f суммы неограниченно увеличивается, то согласно центральной предельной теореме распределение нормированного отношения 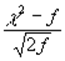 сходится к стандартному нормальному распределению:

,

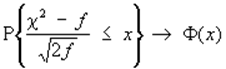где

.

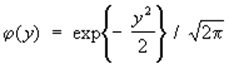 В математической статистике «Хи-квадрат» распеделение используется для построения интервальных оценок и статистических критериев. Если Y₁,..., Y_n — случайные величины, представляющие собой результаты независимых измерений неизвестной постоянной а, причём ошибки измерений Y_i — а независимы, распределены одинаково нормально и

Е (Y_i — a) = 0, Е (Y_i — а)² = ,

то статистическая оценка неизвестной дисперсии , выражается формулой

,

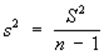где

, .

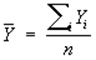  Отношение S²/, подчиняется «Хи-квадрат» распеделению