Корреляционный анализ - метод, позволяющий обнаружить зависимость между несколькими случайными величинами.
Допустим, проводится независимое измерение различных параметров у одного типа объектов. Из этих данных можно получить качественно новую информацию - о взаимосвязи этих параметров.
Например, измеряем рост и вес человека, каждое измерение представлено точкой в двумерном пространстве:
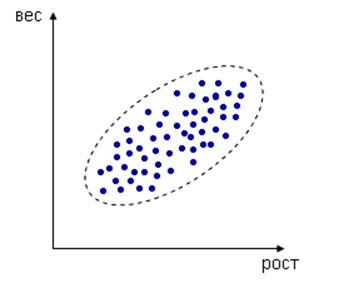
Несмотря на то, что величины носят случайный характер, в общем наблюдается некоторая зависимость - корреляция.
В данном случае это положительная корреляция (при увеличении одного параметра второй тоже увеличивается). Возможны также такие случаи:
|
Отрицательная корреляция:
|
Отсутствие корреляции:
|
Корреляцию необходимо охарактеризовать численно, чтобы, например, различать такие случаи:
|
|
|
Для этого вводится коэффициент корреляции.
Что же такое коэффициент корреляции?
Предположим, что мы измеряем две величины ![]() и
и ![]() ,
характеризующие два различных экспериментальных образца под номерами 1 и 2.
Обозначим результаты измерений на первом образце
,
характеризующие два различных экспериментальных образца под номерами 1 и 2.
Обозначим результаты измерений на первом образце ![]() , а на
втором -
, а на
втором - ![]() .
.
Можно проделать эти операции для любого числа
образцов, например ![]() и
получить набор
и
получить набор ![]() парных
наблюдений
парных
наблюдений ![]() ,
, ![]() ,…,
,…, ![]() .
.
Обозначим среднее значение величин ![]() - через
- через
![]() , а
, а ![]() через
через ![]() и
рассчитаем отклонения каждой пары наблюдений от их средних. Так для
и
рассчитаем отклонения каждой пары наблюдений от их средних. Так для ![]() -го
образца они равны:
-го
образца они равны:
![]() .
.
Эти отклонения можно представить ![]() точками
на диаграмме: пересечению осей соответствует точка
точками
на диаграмме: пересечению осей соответствует точка ![]() - нуль
отклонений. Проделав это для конкретного множества данных, получим картину
рассеяния данных.
- нуль
отклонений. Проделав это для конкретного множества данных, получим картину
рассеяния данных.
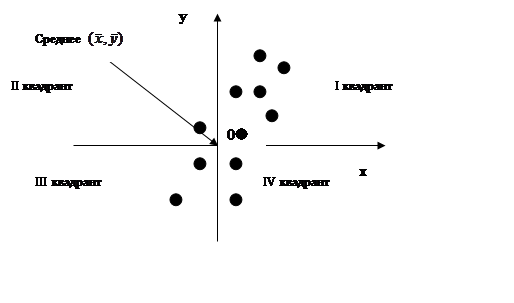 |
Наши оси делят плоскость на четыре квадранта, занумерованных, как показано на рисунке. Большинство наблюдений лежит в I и III квадрантах, и лишь немногие — во II и IV. Наблюдения в I и III квадрантах соответствуют значениям х выше среднего, связанным со значениями у выше среднего, и значениям х ниже среднего, связанным со значениями у ниже среднего.
Удобно ввести сокращенные обозначения для
отклонений величин от средних значений. Отклонения для ![]() -го
образца запишутся в виде
-го
образца запишутся в виде ![]() и
и ![]() , т.е.
, т.е.
![]()
Для всех точек из I квадранта ![]() и
и ![]() -
положительны, и потому их произведение -
также положительно.
-
положительны, и потому их произведение -
также положительно.
В III квадранте ![]() и
и ![]() -
отрицательны, так что их произведение снова положительно.
-
отрицательны, так что их произведение снова положительно.
Для тех немногих точек, которые лежат во II и IV квадранте, одно из отклонений положительно, а другое отрицательно, и потому их произведение отрицательно.
Если сложить эти
произведения для всех п точек и обозначить
результат через ![]() получим:
получим:
![]() , или
, или 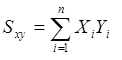
Величина ![]() называется суммой произведений отклонений от среднего. Если точки попадают преимущественно в I
и III квадранты, сумма велика и положительна, так как положительно
большинство слагаемых. Если большинство точек лежит во II и IV квадрантах, сумма велика и отрицательна. Если же точки рассеяны
равномерно по всем квадрантам, то слагаемые стремятся взаимно сократить друг друга, и сумма
оказывается близкой к нулю. Ясно, что
значение
называется суммой произведений отклонений от среднего. Если точки попадают преимущественно в I
и III квадранты, сумма велика и положительна, так как положительно
большинство слагаемых. Если большинство точек лежит во II и IV квадрантах, сумма велика и отрицательна. Если же точки рассеяны
равномерно по всем квадрантам, то слагаемые стремятся взаимно сократить друг друга, и сумма
оказывается близкой к нулю. Ясно, что
значение ![]() зависит
как от значения
зависит
как от значения ![]() , так
и от «разброса» наблюдаемых значении х и
у.
, так
и от «разброса» наблюдаемых значении х и
у.
Чтобы получить
меру этой связи, независимую от разброса
и числа наблюдении, разделим 5.\т на меру разброса, которая сама растет с числом наблюдений. Обычно в качестве таковой берут меру, построенную на сумме
квадратов отклонений значений х и у от их средних, т. е. 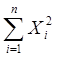 и
и 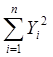 .Мы же фактически будем делить на корень квадратный из произведения
.Мы же фактически будем делить на корень квадратный из произведения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.