Другие предметы \ Статистика

Приобретение практических навыков оценки математического ожидания по заданной выборке случайной величины

Страницы работы

5 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Фрагмент текста работы

Лабораторная работа №5

Цель работы - приобретение практических навыков оценки математического ожидания по заданной выборке случайной величины.

ОБЩИЕ СВЕДЕНИЯ

Для проверки гипотезы о нормальном характере распределения используют критерий «Хи квадрат» К. Пирсона (лабораторная работа №4).

Распределение «хи квадрат»К. Пирсона

Пусть - нормальные независимые случайные величины, причем математическое ожидание каждой из них равно нулю, а среднее квадратическое отклонение – единице. Тогда сумма квадратов этих величин распределена по закону («хи квадрат») 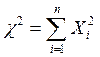с степенями свободы; если же эти величины связаны одним линейным соотношением, например 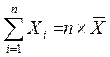, то число степеней свободы равно .

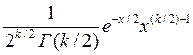Плотность этого распределения 0, при

при

где 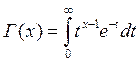-гамма-функция, в частности

Отсюда видно, что распределение определяется одним параметром – числом степеней свободы .

С увеличением числа степеней свободы распределение медленно приближается к нормальному распределению.

Распределение Стьюдента

Пусть X₁,..., X_n – независимые случайные величины, одинаково нормально распределённые, причем , , где а и s > 0. Тогда отношение 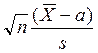подчиняется закону Стьюдента с степенями свободы

(здесь 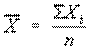и ).

$\begin{figure}...\end{figure}$

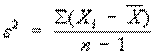Плотность распределения Стьюдента по сравнению с плотностью стандартного нормального распределения.

Это свойство было впервые (в 1908г.) использовано для решения важной задачи классической теории ошибок У. Госсетом (Англия), писавшим под псевдонимом Стьюдент (Student). Суть этой задачи заключается в проверке гипотезы: а = a₀ (a₀ = заданное число, дисперсия s² предполагается неизвестной).

Гипотезу а =a₀ считают не противоречащей результатам наблюдений X₁,..., X_n, если справедливо неравенство 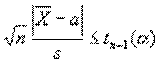, в противном случае гипотеза а = а₀ отвергается (так называемый критерий Стьюдента). Критическое значение t = t_n-1(a) представляет собой решение уравнения S_n-1(t) = 1 –,a — заданный уровень значимости (0 < a < ). Если проверяемая гипотеза а = а₀ верна, то критерий Стьюдента, соответствующий критическому значению t_n–1(a), может её ошибочно отвергнуть с вероятностью а.

Свойства распределения Стьюдента:

Симметричность.

Если случайная величина имеет распределение Стьюдента ${\mathsf T}_k$ с степенями свободы, то и имеет такое же распределение.

Асимптотическая нормальность.

Распределение Стьюдента ${\mathsf T}_k$ слабо сходится к стандартному нормальному распределению при $k\to\infty$ .

Оценкой математического ожидания нормально распределенной случайной величины является выборочное среднее 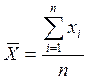, выборочную дисперсию вычисляют по формуле 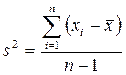(лабораторная работа №2).

Найдя среднее квадратичное отклонение выборки , можно легко рассчитать другую величину, разделив на корень квадратный из числа наблюдений .

Величина представляет оценку стандартной ошибки, которую иногда называют просто стандартной ошибкой среднего, или стандартным отклонением.

Чтобы проверить, подтверждает ли выборочное среднее предположительное значение математического ожидания , рассмотрим величину модуля разности . Поскольку будет сильно меняться от выборки к выборке, разумно взять отношение к некоторой мере разброса. Выбрав в качестве таковой стандартную ошибку среднего, вычислим статистику .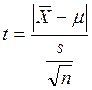

Большие значения бросают тень на гипотезу, что - правильное математическое ожидание.

Для осуществления проверки нужно решить, попадает ли значение в критическую область. Для этого прибегают к помощи таблиц. Эти таблицы также зависят от числа степеней свободы.

Аналогом фиксации ожидаемого значения в статистике является фиксирование в -статистике. Если фиксировано, фиксирована и сумма, и если мы знаем значения наблюдений, мы можем вычислить одно оставшееся, вычитая их сумму из полной суммы. Таким образом, мы приписывает число степеней свободы .

В приложении Б к ГОСТ Р50779.21-96 представлены значения квантилей распределения Стьюдента. Таблица дает минимальные значения на установленных уровнях для указанных степеней свободы.

В таблице значение - заданная надежность; (1 - a) - доверительная вероятность, где a, 0 < a < 1, - уровень значимости при проверке гипотез.

Пусть = a - неизвестная величина, а дисперсия известна. Сформируем гипотезу по заданному числу . Если , которым мы пользуемся при расчете -статистики, есть истинное