1. Модели пространственного размещения точечных объектов.
Моделирование структуры пространственных характеристик явлений привлекло к себе внимание на самых первых этапах математизации географии. Отчасти этим и объясняется большое количество исследований, посвященных изучению отдельных структурных элементов с помощью простейших математических моделей и географических карт, используемых для пространственного координирования явлений на начальном этапе исследований или для фиксации результатов.
Наиболее многочисленны примеры конструирования моделей, отображающие отдельны стороны размещения точечных географических объектов. Такие исследования характеристик топологии точечных объектов, в качестве которых исследуются населенные пункты, магазины, кинотеатры, школы, промышленные предприятия и т .д., столь разнообразны, что мы ограничимся лишь кратким их перечислением.
Прежде всего, следует назвать исследования точечных сетей как правильных, «идеальных» решеток Кристаллера. Рассмотрим суть метода.
По адресной карте ( карте людности населений, топографической карте и др.) с помощью цифрователя измеряются прямоугольные координаты Х и У всех пунсонов, фиксирующих положение населенных пунктов.
В качестве эталонной, абсолютно равномерной сети точек будем считать гексагональное их расположение по территории. Для гексагональной решетки характерно то, что если взять любой ее узел, то расстояния между данным узлом и окружающими ее шестью ближайшими точками будут равны. Кроме того, все шесть расстояний между соседними точками окружения также будут равны им по длине, т.е. если все эти двенадцать расстояний окажутся равными, то такая сеть считается абсолютно равномерной. В качестве показателя равномерности можно использовать коэффициент вариации:
V=![]() (1.1)
(1.1)
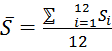 ,
σ=
,
σ=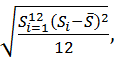 (1.2)
(1.2)
Где ![]() –
расстояние между шестью окружающими центральный пункт точками, а также между
данными точками и центральной точкой.
–
расстояние между шестью окружающими центральный пункт точками, а также между
данными точками и центральной точкой.
Величина V для любого угла гексагональной решетки будет равна нулю. Иными словами, нуль – показатель полной равномерности сети. Степень увеличения коэффициента вариации может быть принята за величину неоднородности размещения точек. В пределе величина V может достигать значения 100.
Взяв первую (начальную) точку, несложно, по измеренным координатам Х и У, вычислить расстояния между ней и другими в окружении точками и выбрать шесть наикратчайших. Далее для выбранных шести точек по координатам определяются шесть расстояний между ними.
Таким образом, выбранные двенадцать расстояний используются для расчета показателя равномерности в окружении первой точки по формуле (1.1). Затем аналогичные расчеты производятся для второй точки и т.д. В результате для всех населенных пунктов вычисляются величины равномерности размещения пунктов в ближайшем их окружении. Останется лишь нанести данные значения на карту и в виде изолиний отобразить картину варьирования вычисленных показателей по территории.
Для того чтобы не искажать величин коэффициентов на краях исследуемого региона, в производимые вычисления следует включать и пункты сопредельных территорий.
Также заметим, что ячейки гексагональной
сети, соблюдая принцип подобия, могут быть увеличены или уменьшены, но величина
коэффициента вариации все равно будет равна нулю и свидетельствовать об
абсолютной равномерности. Однако бывает целесообразно в одном показателе
учитывать не только степень равномерности, но и величину расстояний между
пунктами, например при планировании размещений учреждений обслуживания. Для
этих целей подсчитывается среднее расстояние (![]() между
всеми пунктами исследуемой территории, и эта величина значение d в формуле (1.1). После такой модификации происходит существенная трансформация
картины равномерности.
между
всеми пунктами исследуемой территории, и эта величина значение d в формуле (1.1). После такой модификации происходит существенная трансформация
картины равномерности.
2. Конструирование тематической карты равномерности размещения населенных пунктов N-ой области.
По адресной карте N-ой области измеряются прямоугольные координаты
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.